Учебное пособие 999

где τi = max {Tj ,Tl ,Tk } - минимально возможный срок начала работы αi , которая опирается на работы α j , αl , αk и не может

начаться прежде, чем не будет завершена работа, которая заканчивается позже всех.

Работы αi , из длительностей которых составлено

минимальное время завершения комплекса работ Т, называются критическими работами. Чтобы найти критические работы, а следовательно и критический путь, надо найти работу αi , для которой время окончания T i

максимально; эта работа и будет критической. Далее следует

Необходимо найти max. Это будет вторая критическая работа от конца и т. д.

2°. Пусть общее время выполнения работ T = ∑ti нас не

(kp)

устраивает и требуется его сократить до времени Т0 .

Очевидно, что надо форсировать критические работы. Вложение дополнительных средств x i в работу αi сокращает

i=1

примере 1.2.

3°. Рассмотрим задачу перераспределения уже имеющихся средств между отдельными работами. Известно, что количество средств x > 0, снятое с работы αi , увеличивает

время ее выполнения с t i до ti′ = fi (xi ) , а количество средств x , вложенных дополнительно в работу αl уменьшает время ее

2

выполнения до ti ″=ϕi (x) . Сумма средств, снимаемых с каких-

то работ, должна быть равна сумме средств, добавляемых к другим работам, так что

Для решения задачи необходимо, чтобы общий срок выполненного комплекса работ был минимален

4°. Сетевое планирование при случайных временах выполнения работ. При сложении достаточно большого числа независимых случайных величин, распределенных по любым законам, закон распределения суммы близок к нормальному, поэтому МО времени равно сумме

где Ф – функция Лапласа находится из таблицы.

1.1. Пусть дана упорядоченная структурная таблица

3

Построить временный график и найти критические работы. Решение. Для работы первого ранга имеем:

τ1 = 0 ; τ2 = 0 ;τ3 = 0 ;T1 = t1 =10 ;T2 = t2 = 5 ;T3 = t3 =15 .

Работа α4 опирается на работы α1 ,α2 , т.е. она может

T7 =τ7 +t7 = 46 +8 = 54 .

α8 :τ 8= max{T3 ,T5 ,T6 }= max{15,34,46}= 46; T8 =τ8 +t8 = 46 + 25 = 71.

α9 : τ9 = max{T7 }= 54 ; T9 =τ9 +t9 = 54 +30 = 84 .

α10 :τ10 = max{T5 ,T8 }= max{34,71}= 71 ;

T10 =τ10 +t10 = 71 +8 = 79 .

Время окончания работы равно максимальному времени окончания T = 84 и α9 последняя критическая работа.

Поскольку α9 опирается на α7 , то следующая критическая

4

работа α7 . Так как большая работа, на которую опирается α7 будет α6 , то α6 следующая критическая работа, α6 - опирается

на α4 , а α4 - на α1 . Таким образом, α1 , α4 , α6 , α7 , α9 - критические работы. Сетевой график показан на рисунке

Рис. 1

1.2. Комплекс работ задан структурно-временной таблицей

Т3 = 8 ; Т4 =Т1 +t4 = 40; T5 = T1 +t5 = 30 ; T6 = T1 +t6 = 25 ;

T7 = T6 +t7 = 30 ; T8 = T4 +t8 = 50.

Критические работы будут α1 , α4 , α8 . Время окончания комплекса работ равно Т = Т1 +Т4 +Т8 = 50.

Уменьшим это время до Т0 = 40 . Известно, что в работу αi

5

неравенствах ограничений (3), (4), т.е. налицо задача линейного программирования.

Решая задачу симплекс методом, находим, что Lmin = 5 / 3 и оптимальным решением будет вложение x4 = 5 / 3 в работу α4 .

2. ОПТИМИЗАЦИЯ РАЗМЕЩЕНИЯ УЗЛОВ ПОЧТОВОЙ СВЯЗИ

1°. При проектировании городской почтовой связи необходимо решить, где разместить узлы связи и как организовать их транспортные связи с опорными пунктами города (вокзалами, аэропортами, пристанями, типографиями и т.д.).

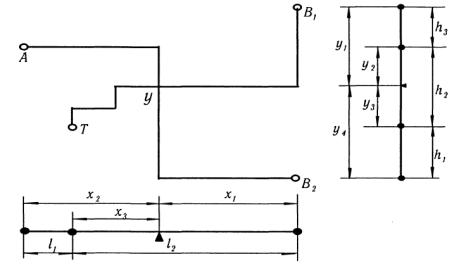
Пусть в городе имеется узел связи (У), два вокзала ( В1 , В2 ),

типография (Т) и аэропорт (А) (рис.2).

В качестве критерия оптимизации выберем минимум пробега транспорта между узлом и опорным пунктом. Обозначим за N1 − число рейсов за сутки между каждым из

6

вокзалов и узлом; N2 − между аэропортом и узлом; N3 − между узлом и типографией.

прямоугольную сеть. Протяженность каждого маршрута представим как сумму расстояний по оси x и по оси y.

Обозначим через x1 расстояния по горизонтали между каждым из вокзалов и узлом; x2 − между аэропортом и узлом; x3 − между типографией и узлом. Величины l1 и l2 заданы.

Целевая функция, минимум которой требуется найти, будет иметь вид

L1 = 2N1 x1 + N2 x2 + N3 x3 .

Система ограничивающих условий будет

x1 + x2 ≥ l1 +l2 ; x1 + x3 ≥ l2 ; x2 + x3 ≥ l1.

Полученная модель является моделью задачи линейного программирования.

Рассмотрим по оси y. Обозначим через y1 − расстояние между вокзалом 1 и узлом; y2 − между аэропортом и узлом;

7

y3 − между типографией и узлом; y4 − между вокзалом 2 и узлом. Целевая функция, минимум которой необходимо найти,

результате решения двух задач определяется общая

8

Математическая модель относительно оси y запишется в виде

L2 =10y1 +8y2 + 6 y3 +10 y4 ;

y1 + y4 ≥15; y1 + y3 ≥10; y2 + y3 ≥ 6; y2 + y4 ≥11.

Через базисные переменные

L2 = 0 −(−10 y1 −8y2 −6 y3 −10y4 ),

y5 = −15 −(−y1 − y4 ); y6 = −10 −(−y1 − y3 ); y7 = −6 −(−y2 − y3 ); y8 = −11 −(−y2 − y4 ).

Составим таблицу

9