
Учебное пособие 999
.pdf
|
C64 |
= min(C64 ,C63 +C34 ) = min(∞,3 +5) = 8. |
|
|
|
|||||
|
Матрица, полученная после третьей итерации, будет |
|
||||||||
|
|
1 |
|
2 |
3 |
4 |
|
5 |
|
6 |
|
1 |
0 |
|
1 |
4 |
9 |
|
5 |
|
3 |
|
2 |
1 |
|
0 |
3 |
8 |
|
4 |
|
2 |
|
3 |
4 |
|
3 |
0 |
5 |
|
1 |
|
3 |
|
4 |
9 |
|
8 |
5 |
0 |
|
1 |
|
8 |
|
5 |
5 |
|
4 |
1 |
1 |
|
0 |
|
3 |
|
6 |
3 |
|
2 |
3 |
4 |
|
3 |
|
0 |
|
Приведем расчет для k= 5 только тех элементов, которые |
|||||||||
|
меняются |
|
|
|
|
|
|
|
||
|
C14 = min(C14 ,C15 |
+C54 ) = min(9,5 +1) = 6; |
|
|
|
|||||
|
C24 = min(C24 ,C15 |
+C54 ) = min(8,4 +1) = 5; |
|
|
|
|||||
|
C34 = min(C34 ,C35 |
+C54 ) = min(5,1+1) = 2; |
|
|
|
|||||
|
C41 = min(C41 ,C45 |
+C51 ) = min(9,1 +5) = 6; |
|
|
|
|||||
|
C42 = min(C42 ,C45 |
+C52 ) = min(8,1 + 4) = 5; |
|
|
|
|||||
|
C46 = min(C46 ,C45 |
+C56 ) = min(8,1 +3) = 4. |
|
|
|
|||||
|
Таким образом, кратчайшие пути между всеми узлами |
|||||||||
|
|
|
|
|
|
4 |
|
|
|
|
|
|
1 |
|
2 |
3 |
|
5 |
|
6 |
|
|
1 |
0 |
|
1 |
4 |
6 |
|
5 |
|
3 |
|
2 |
1 |
|
0 |
3 |
5 |
|
4 |
|
2 |
|
3 |
4 |
|
3 |
0 |
2 |
|
1 |
|
3 |
|
4 |
6 |
|
5 |
2 |
0 |
|
1 |
|
4 |
|
5 |
5 |
|
4 |
1 |
1 |
|
0 |
|
3 |
|
6 |
3 |
|
2 |
3 |
4 |
|
3 |
|
0 |
4.2. Для сети, представленной на рис. 3, найти кратчайшие пути от вершины а1 до остальных.
Решение. Результаты расчетов приведены в таблице.
20

k |
p |
l1 |
l2 |
l 3 |
l 4 |
l 5 |
l 6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
0 |
∞ |
∞ |
∞ |
∞ |
∞ |
2 |
2 |
0 |
1 |
∞ |
∞ |
∞ |
5 |
3 |
6 |
0 |
1 |
4 |
∞ |
7 |
3 |
4 |
3 |
0 |
1 |
4 |
∞ |
6 |
3 |
5 |
4 |
0 |
1 |
4 |
9 |
5 |
3 |
6 |
5 |
0 |
1 |
4 |
6 |
5 |
3 |
В первом столбце дается номер итерации, во втором — номер вершины, получающей на данной итерации постоянную пометку, а в остальных — величины пометок для каждой вершины. Столбец выделяется жирными линиями, начиная с той итерации, на которой пометка соответствующей вершины стала постоянной. Рассмотрим порядок расчета.
1. На первой итерации пометка первой вершины постоянная и равна l1 = 0 , пометки остальных вершин
временные и равны li = ∞.
2. Соседями вершины а1 является а2 и а6 . Временные
пометки этих вершин равны
l2′ = min(∞,0 +1) =1; l6′ = min(∞,0 +5) = 5.
Выбираем минимальную из них l2′ =1; p = 2; l p =1.
3. На третьей итерации соседями вершины а2 являются вершины a3 , a5 , a6 . Временные пометки этих вершин
l2′ = min(∞,1 +3) = 4; |
l5′ = min(∞,1 + 6) = 7; |
||
l6′ = min(5,1 + 2) = 3. |
|
|
|
Минимальная из них l6′ |
становится |
постоянной l6 = 3, |
|
p = 6. |
|
|
|
4. Соседями вершины |
а6 являются |
a3 , a5 . Временные |
|
пометки этих вершин l3′ |
= min(4,3 +3) = 4; |
l5′ = min(7,3 +3) = 6. |
|
Минимальная из них l3′ |
становится постоянной l3 = 4, p = 3. |
||
|
|
21 |
|
5. На пятой итерации соседями вершины a3 являются вершины a4 , a5 . Найдем временные пометки этих вершин
l4′ = min(∞,4 +5) = 9; l5′ = min(6,4 +1) = 5.
Минимальная из них l5′ = 5 становится постоянной l5 = 5, p = 5.
6. Вершина a5 соседствует с вершиной a4 , временная пометка которой l4′ = min(9,5 +1) = 6, p5 = 4.
Таким образом, кратчайшие пути от первой вершины ко всем остальным приведены в вершинах выделенных столбцов и совпадают с первой строкой матрицы алгоритма Флойда предыдущей задачи.
5. АЛГОРИТМЫ ОПРЕДЕЛЕНИЯ МАКСИМАЛЬНОГО ПОТОКА
1°. Пусть в сети имеется единственный источник a0 и единственный сток an . Обозначим положительным числом bij
пропускную |
способность дуги от |
ai к a j , |
а |
за bji − |
|||
пропускную способность дуги от a j |
к ai ,причем выполнение |
||||||
равенства |
bij = bji |
не |
обязательно. |
Потоком |
в |
сети из |
|
источника |
a0 |
в |
сток |
an |
называется |
множество |
|
неотрицательных чиселxij , поставленных в соответствие дугам
|
|
−υ, j = 0, |
|
|
|
|
j ≠ 0, n, |
сети, таких, что ∑xij − ∑x jk = 0, |
|||
i |
k |
υ, |
j = n, |
|
|
||
где 0 ≤ xij ≤ bij ; число υ ≥ 0 называется величиной потока.
2°. Пусть начальные пропускные способности дуг заданы. Выберем некоторый начальный поток, например, нулевой.
Алгоритм работает следующим образом.
22

1. Выберем путь из a0 в an положительной пропускной способности θ , гдеθ − минимальная величина из пропускных
способностей |
дуг. |
Источник |
a0 считается |
вначале |
помеченным, но не просмотренным, а все остальные узлы не помеченными.
2. Выбрать любой помеченный, но не просмотренный узел
ai .
3. Всем узлам a j , для которых bij ≥ 0 , приписать пометки ( i, j ) и считать их помеченными. Считать узел a0 просмотренным. Если при этом сток an оказался помеченным, то по пометкам легко восстановить искомый путь из a0 в an .
В противном случае следует перейти к шагу 2. Если это невозможно, то искомого пути не существует.
4. |
Пусть |
(a0 , ai ), |
(ai , ai |
), …, (ai |
, ai |
m |
) — найденный |
|||
|
|
|
|
|
1 |
1 |
2 |
m−1 |
|
|
путь. Тогда для каждой дуги (aik , aik +1 ) ^), |
входящей в этот |
|||||||||
путь, следует выполнить операторы: |
|
|
|
|||||||
xik ik +1 |
:= xik ik +1 |
+θ; bik ik +1 |
:= bik ik +1 −θ; |
|
|
|
||||
bi |
i |
:= bi |
k |
i |
+θ; υ :=υ +θ. |
|
|
|
|
|
|
k +1 k |
|
+1 k |
|
|
|
|
|
|
|
Далее переходим к шагу 1. Если пути положительной пропускной способности не существует, то полученный поток является максимальным.
5.1. В области имеется семь городов, соединенных дорогами. Граф задачи показан на рис.4.
Рис. 4
23

На каждой дуге (ai , a j ) около узла ai указано
максимальное (за один день) число мешков с корреспонденцией, которые можно перевезти от ai к a j ,
а около узла a j — максимальное число мешков, которые можно перевезти из a j в ai . Найти максимальное число мешков, которые можно перевезти из a0 в an .
Решение. Пусть начальный поток задан числами
υ = x02 = x25 = x56 = 5 (потоки по остальным дугам равны нулю). После изменения пропускных способностей дуг bik ik +1 получается сеть.
Далее выбираем путь a0 → a1 → a4 → a6 , где θ = 3
минимальная величина из пропускных способностей. Изменяя пропускные способности дуг, получим
24

На следующем шаге выбираем путь
a0 → a1 → a2 → a4 → a6 ,θ =1,
тогда граф примет вид
Далее a0 → a2 → a4 → a6 , θ = 2 и граф будет
Следующий шаг a0 → a3 → a5 → a4 → a6 , θ =1
Далее a0 → a3 → a2 → a4 → a6 , θ =1
25
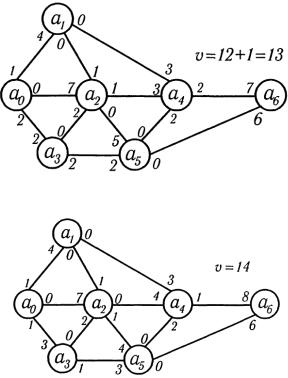
Наконец, a0 → a3 → a5 → a2 → a4 → a6 , θ =1
Поскольку положительной пропускной способности нет, то полученный поток является максимальным.
6. ЗАДАЧА ЗАМЕНЫ ОБОРУДОВАНИЯ
Покупная цена нового оборудования известна и равна S . Известны затраты на эксплуатацию (уход, ремонт и т. д.) в соответствующие периоды (1, 2,..., t,..., п). Пусть периоды равны, а затраты в период t будут Ct . В результате старения
балансовая цена оборудования непрерывно падает. Обозначим ее за St . Считаем, что Ct и St экспоненциально зависят от t
C |
a |
0 |
(eλt −1); |
S |
t |
= b e−μt . |
t |
|
|
|
0 |
Средние затраты равны
26

Y (t) = (S + ∑t Ct − St ) / t,
t =1
Y (t) = (S + a0 (eλt −1) −b0 e−μt ) / t = (a0 (eλt −1) + S(1 −e−μt )) / t.
Отсюда
|
dY |
= |
(a |
λe λt + Sμe−μt |
)t − a |
0 |
(eλt |
−1) − S(1 −e−μt ) |
= 0. |
||
|
|
0 |
|
|
|
|
|
|
|||
|
dt |
|
|
t 2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
Преобразуя, будем иметь |
|
|
|
|
|
|
|
||||
a0 (λteλt −eλt +1) = S(1 −e−μt − μte−μt ). |
|
|
|
||||||||
Если |
|
|
обозначить |
|
|
Y |
= a |
0 |
(λteλt +1) |
и |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
Y2 = S(1 −e−μt − μte−μt ), то точка пересечения этих кривых и
даст искомое время t, когда следует произвести замену оборудования.
7. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
1°. Метод наименьших квадратов заключается в том, что из данного множества функций y = f (x) выбирается та, для
которой сумма квадратов отклонений опытных значений от расчетных является наименьшей.
Подбор параметров функции y = f (x) делается после
определения вида функции. Вид функции выбирается из графического изображения опытных данных таким образом, чтобы график функции наиболее точно отражал расположение опытных данных на графике. Пусть дана таблица значений переменных xi и соответствующих им значений yi .
xi |
x1 |
x2 |
… |
xn |
yi |
y1 |
y2 |
… |
yn |
Рассмотрим некоторые простейшие виды функций.
2°. Линейная функция y = ax +b . Нормальная система для определения коэффициентов a и b имеет вид
27
n |
|
n |
n |
|
a∑xi |
2 +b∑xi = ∑xi yi ; |
|
||
i=1 |
|
i=1 |
i=1 |
|
|
n |
|
n |
|
a∑xi +bn = ∑yi . |
(1) |
|||
|
i=1 |
|
i=1 |
|
3°. Квадратичная функция y = ax2 +bx + c . |
Нормальная |
|||
система для определения коэффициентов a , b и с имеет вид
|
|
a∑xi 4 +b∑xi 3 + c∑xi 2 = ∑xi 2 yi ; |
|
|||||||||||||||||||
|
|
a∑xi 4 +b∑xi 3 + c∑xi 2 = ∑xi 2 yi ; |
|
|||||||||||||||||||
|
|
|
|
a∑xi |
2 +b∑xi |
+ cn = ∑yi . |
|
|
(2) |
|||||||||||||
4°. |
Гипербола |
вида |
y = a + |
b |
. |
|
Нормальная |
система |
для |
|||||||||||||
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|||
определения параметров a и b имеет вид |
|
|
|
|||||||||||||||||||
|
|
|
|
a∑ |
1 |
+b∑ |
|
1 |
|
|
= ∑ |
yi |
; |
|
|
|
|
|||||
|
|
|
|
xi |
|
2 |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
xi |
|
|
xi |
|
|
|
|||||||
|
|
|
|
na +b∑ |
|
1 |
= ∑yi . |
|
|
(3) |
||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
xi |
|
|
|
|
|
|
|
|
|||||
7.1. |
|
Результаты |
экспериментальных |
исследований |
||||||||||||||||||
представлены таблицей |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
xi |
|
1 |
|
2 |
|
|
|
3 |
|
|
|
|
|
|
4 |
|
|
5 |
|
6 |
||
yi |
|
13 |
|
8 |
|
|
|
4 |
|
|
|
|
|
|
1 |
|
|
-2 |
|
-9 |
||
Полагая, что зависимость линейная, найти значения параметров функции y = ax +b .
Решение. Воспользуемся методом наименьших квадратов. При составлении системы нормальных уравнений (1) суммирование удобнее выполнять в табличной форме
28

i |
xi |
yi |
xi 2 |
xi yi |
1 |
1 |
13 |
1 |
13 |
2 |
2 |
8 |
4 |
16 |
3 |
3 |
4 |
9 |
12 |
4 |
4 |
1 |
16 |
4 |
5 |
5 |
-2 |
25 |
-10 |
6 |
6 |
-9 |
36 |
-54 |
∑ |
21 |
15 |
91 |
-19 |
Система нормальных уравнений примет вид
91a + 21b = −19,21a + 6b = 5.
Из решения этой системы получим a = −14335 ; b = 845 .
Зависимость между x и y представляется в виде y = −14335 x + 845 .
7.2. Результаты опыта представлены таблицей
xi |
0 |
1 |
2 |
3 |
4 |
yi |
1 |
2 |
4 |
7 |
11 |
Найти зависимость между переменными.
Решение. Прибрасывая опытные данные на графике, считаем, что зависимость между ними квадратичная.
Воспользуемся методом наименьших квадратов. При составлении системы нормальных уравнений (2) суммирование представим в табличной форме
29
