
Учебное пособие 995
.pdfФункция называется синус-преобразованием Фурье
для функции f x .
60
3.9. Интеграл Фурье в комплексной форме
В интеграле Фурье (3.34) в скобкахстоит четная функция от ω, следовательно, она определена и при отрицательных значениях ω. Следовательно, формулу (3.34) можно переписать так:
|
1 |
|
|
|
|
|
|
f x |
|
|
f t cos t x dt |
|
|||
|
|
|
|
(3.42) |
|||
|
|
||||||
2 |
d . |
||||||
|
|
|
|
|
|
||
Далее рассмотрим следующее выражение:
|
|
|
|
|
|
|
|
f t sin t x dt |
|
||
|
|
|
(3.43) |
||
|
d 0. |
||||
|
|
|
|
||
Выражение, стоящее слева, тождественно равно нулю потому, что функция от ω, стоящая в скобках, есть нечетная функция, а интеграл от нечетной функции в пределах, симметричных относительно нуля, равен нулю.
Умножим члены равенства (3.43) на |
|
i |
и сложим с со- |
|||||||||||||
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|||
ответствующими частями равенства (3.42). Тогда получим: |
|
|||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f x |
2 |
f t cos t x isin t x dt |
, |
|||||||||||||
|
d |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
или, применяя формулу Эйлера: |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
i t x |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
f x 2 |
f t e |
|
dt |
|
(3.44) |
||||||||
|
|
|
|
|
d . |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Правая часть в формуле (3.44) называвется интегралом Фурье в комплексной форме для функции f x .
Перепишем формулу (3.44) в следующем виде:
|
|
1 |
|
|
|
|
|
|
f x |
f t e |
i t |
|
i x |
|
|||
|
|
|
dt |
|
|
d , |
||
|
|
|
||||||
2 |
|
e |
|
|||||
|
|
|
|
|
|
|
|
|
или
61
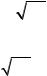
f x C ei xd , |
(3.45) |
|||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
C |
|
f t e |
i t |
dt . |
(3.46) |
|
2 |
|
|||||
Здесь ω называется волновым числом, оно принимает все значения от –∞ до +∞. Спектр волновых чисел называется не-
прерывным спектром. Функцию C называют спектральной
плотностью или спектральной функцией.
Равенства (3.45) и (3.46) можно переписать в симметричной форме:
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||||
F |
|
|
|
|
|
|
f t e |
i t |
dt , |
(3.47) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
2 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||
f x |
|
|
|
|
F |
|
e |
i x |
d . |
(3.48) |
|||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
2 |
|
|
|
||||||||||||||||
Функция F , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
определяемая формулой (3.47), называ- |
|||||||||||||||||||
ется преобразованием |
Фурье |
для |
функции |
f x . Функция |
|||||||||||||||
f x , определяемая формулой (3.48), называеся обратным пре-
образованием Фурье для функции F .
Преобразование Фурье (3.47) связано с косинус- и синуспреобразованиями Фурье (3.38) и (3.40) формулой:
F F i .
3.10. Ряд Фурье по ортогоналной системе функций
Бесконечная система функций 1 x , 2 x ,..., n x ,... на-
зывается ортогональной на отрезке a,b , если при любых n k
62
выполняеся равенство
b
|
|
|
|
|
n x k x dx 0. |
|
|
|
(3.49) |
|||||||||
При этом |
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
b |
n |
|
2 dx 0. |
|
|
|
|
|
|
|||||||
|
|
|
x |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Пример 1. Система функций 1, cos x, sin x, cos 2x, sin 2x, …, |
|||||||||||||||||
cos nx, sin nx, … ортогональна на отрезке ; . |
|
|
|
|||||||||||||||
|
Пример 2. Система функций 1, |
cos |
|
x, |
sin |
|
x, cos |
2 |
x , |
|||||||||
|
|
|
||||||||||||||||
|
2 |
|
|
n |
|
|
n |
|
|
l |
|
l |
|
l |
||||
sin |
x, …, |
cos |
x, sin |
x, … |
ортогональна на |
отрезке |
||||||||||||
|
l |
|
l |
|
l |
|
|
|
|
|
|
|
|
|
|
|
||
l;l .
Пусть функция f x , определенная на отрезке a;b , та-
кова, что она разагается в ряд по функциям ортогональной системы (3.49), который сходится кданной функции на отрезке
a;b :
|
|
f x cn n x . |
(3.50) |
n 0 |
|
Найдем коэффициенты cn . Умножим обе части равенства
(3.50) на k x и проинтегрируем в пределах от a до b. Учиты-
вая равенства (3.49), получим
b |
b |
f x k x dx ck k2 x dx,
a |
a |
откуда
63
b
c |
|
f x k x dx |
. |
(3.51) |
|
a |
|||||
b |
|||||
k |
|
|
|
||
|
|
k2 x dx |
|
|
|
|
|
a |
|
|
|
Коэффициенты ck, вычисленные по формулам (3.51), на- |
|||||
зываются коэффициентами Фурье функции |
f x по системе |
||||
ортогонаьных функций k x . Ряд (3.50) называется рядом Фурье по системе функций k x .
В приложениях широко используются системы ортого-
нальных многочленов Лежандра, которые определяются так:
|
|
|
|
1 d |
n |
2 |
1 |
n |
|
||
P |
x 1, |
P |
x |
x |
|
|
n 1,2,... . |
||||
|
|
|
|
|
|
|
|||||
2n n! |
dxn |
|
|||||||||
0 |
|
n |
|
|
|
||||||
Они удовлетворяют дифференциальному уравнению
x2 1 y 2xy n n 1 y 0.
Используются и другие системы ортогональных многочленов.
Задачи для самостоятельного решения
Задача № 1. Разложить в ряд Фурье периодическую с пе-
риодом T 2 |
функцию f x , заданную на отрезке ; . |
|||
1. |
f x |
|
0, |
x 0, |
|
0 x |
|||
|
|
|
x 1, |
|
2. |
f x |
|
2x 1, x 0, |
|
|
0 x |
|||
|
|
|
0, |
|
3. |
f x |
|
0, |
x 0, |
|
0 x |
|||
|
|
|
x 2, |
|
64

4. |
f x |
2x 3, x 0, |
||||||
|
0 x |
|
||||||
|
|
0, |
|
|||||
5. |
f x |
0, |
x 0, |
|||||
|
|
|
|
|||||
|
|
4x 3, 0 x |
|
|||||
Задача № 2. Разложить в ряд Фурье в указанном интервале |
||||||||
периодическую функцию f x |
с периодом 2l . |
|||||||
1. |
f x 2x, |
1 x 1, |
l 1 |
|||||
2. |
f x |
|
x |
|
5, 2 x 2, |
l 2 |
||
|
|
|||||||
3. |
f x 5x 1, 5 x 5, |
l 5 |
||||||
4. |
f x |
0, |
2 x 0, |
|
|
|||
|
, l 2 |
|||||||
|
|
2, |
0 x 2 |
|
|
|||
5. |
f x |
1, |
1 x 0, |
|
|
|||
|
l 1 |
|||||||
|
|
x, |
0 x 1 |
|
|
|||
Задача № 3. Разложить в ряд Фурье функцию f x , заданную в интервале 0; , продолжив ее четным и нечетным образом.
1.f x x2
2.f x ex
3.f x x 2 2
4.f x x 1 2
5.f x sh x . 5
65
4. ЗАДАНИЯ ДЛЯ ТИПОВОГО РАСЧЕТА ПО ТЕМЕ «ФУНКЦИОНАЛЬНЫЕ РЯДЫ»
Задача 1.
Периодический сигнал f(t) разложить в тригонометрический ряд Фурье. Вычертить графики сигнала f(t) и частичных сумм S1(t), S2(t) ряда Фурье.
1.1.f(t) = | t | – 1 на [-2; 2], f(t + 4) = f(t).
1.2.f(t) = 2 + | t | на [-2; 2], f(t + 4) = f(t).
1.3.f(t) = | 1 – t2 | на [-1; 1], f(t + 2) = f(t).
1.4.f(t) = 1 – | t | на [-3; 3], f(t + 6) = f(t).
|
t |
,если-2 t 0 |
||
|
|
|
||
|
2 |
|
, f (t 3 ) f (t). |
|
1.5. f (t) |
|
|||
|
|
|
|
,если0 t |
|
||||
4
1.6f(t) = t2 + t на [-2 ; 2], f(t + 4) = f(t).
|
t,если -3 t 0 |
|
||
1.7 |
|
0,если 0 t |
1 , |
f (t 6) f (t) . |
f (t) |
||||
|
|
1,если 1 t |
3 |
|
|
|
|
||
1.8. f(t) = (t – 1)2 на [-1; 1], |
f(t + 2) = f(t). |
|||
1.9. |
2 t,если-2 t 0 |
|||
f (t) |
1,если0 t 2 |
, f (t 4) f (t) . |
||
|
|
|
||
1.10. f(t) = t2+1 на [-2;2], f(t + 4) = f(t).
66
1.11. |
1,если-2 t 0 |
f (t 4) f (t). |
||
f (t) |
|
, |
||
|
t,если0 t 2 |
|
||
|
|
t,если -1 t 1 |
|
|
1.12. |
|
1,если 1 t 2 |
, f (t 4) f (t). |
|
f (t) |
||||
|
|
|
|
|
|
3 t,если 2 t 3 |
|||
|
|
2 |
,если-2 t 0 |
|
1.13. |
t |
|
f (t 4) f (t). |
|
f (t) |
|
, |
||
|
|
0,если0 t 2 |
|
|
1.14. f(t) = 1 – 2t на [-2 ; 2], f(t + 4) = f(t).
|
|
|
|
2 |
|
2,если-2 t 0 |
|
|
|
|
|
|
||
1.15. f (t) |
|
|
|
|
|
|
, |
f (t |
) |
|||||
|
|
|
|
|
(t ) ,если0 |
t |
|
3 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1.16. f (t) |
|
|
,если-2 t 0 |
, f (t 4) f (t). |
|
|||||||||
2 |
|
|||||||||||||
|
|
|
|
|
|
|||||||||
|
|
|
1 t,если0 t 2 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
t |
,если -2 t |
0 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
1.17. f (t) |
|
|
0,если 0 t |
, f (t 4 ) f (t |
||||||||||
|
|
|
||||||||||||
|
|
|
t,если t 2 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.18. f (t) |
t,если-2 t 0 |
f (t 4) |
f (t). |
|
|
|||||||||
|
|
|
, |
|
|
|||||||||
|
|
t |
2 ,если0 t 2 |
|
|
|
|
|
|
|
||||
f (t).
).
67
|
1 |
,если -3 t 1 |
|
|
|
|
|
2 |
|
||
|
|
f (t 6) f (t). |
|
1.19. f (t) |
1,если 1 t 1 , |
||
2 t,если 1 t 3
1.20. |
t 2,если-1 t 0 |
||||
f (t) |
|
2,если0 t 1 |
|
||
|
|
|
|
||
|
|
2 |
,если-2 t 0 |
|
|
1.21. |
t |
|
, |
||
f (t) |
|
1 |
,если0 t 2 |
||
|
|
|
|
||
|
2 |
|
|||
|
|
|
|
|
|
, f (t 2) f (t).
f (t 4) f (t).
1.22. f(t) = t - t2 на [-2 ; 2], f(t + 4) = f(t).
|
|
|
2 |
,если-2 t 0 |
|
|
1.23. |
1 t |
|
f (t). |
|||
f (t) |
1,если0 t 2 |
, f (t 4) |
||||
|
|
|
|
|||
|
1,если -3 t 1 |
|
|
|||
|
|
2 ,если 1 t 1, |
f (t 6) f (t) |
|||
1.24. f (t) t |
||||||
|
|
1,если 1 t 3 |
|
|
||
|
|
|
|
|||
1.25 |
f(t)= t2 – 2t + 2 на [-3; 3], |
f(t + 6) = f(t). |
|
|||
Задача 2.
Найти аналитическое выражение периодического тока I(t) определенного осциллограммой (см. рисунок). Записать ряд Фурье в действительной форме для I(t).
68

69
