
Задачи оптимизации и планирования. Каверина В.К
.pdfМИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение высшего образования
«Воронежский государственный архитектурно– строительный университет»
В.К. Каверина
ЗАДАЧИ ОПТИМИЗАЦИИ И ПЛАНИРОВАНИЯ
Учебное пособие
Воронеж 2015
УДК 517.15 ББК 22.176я73
К125
Каверина, В.К.
К125 Задачи оптимизации и планирования на сетях: учеб. по-
собие / В.К. Каверина; Воронежский ГАСУ. – Воронеж, 2015. – 62 с.
В учебном пособии излагаются основы теории графов и представлены алгоритмы, предназначенные для решения прикладных задач с помощью теории графов. Разобранные задачи имеют экономическую интерпретацию, а методы их решения находят широкое практическое применение. Каждый раздел сопровождается упражнениями.
Учебное пособие предназначено для магистрантов всех направлений, изучающих курсы дискретной математики и дискретного программирования, включенные в современные образовательные стандарты. Пособие будет полезно магистрантам и аспирантам в качестве дополнительного материала при изучении основ теории графов и задач планирования и оптимизации на сетях.
Ил. 33. Табл. 6. Библиогр.: 11 назв.
УДК 517.15 ББК 22.176я73
Печатается по решению учебно-методического совета Воронежского ГАСУ
Рецензенты:
кафедра высшей математики и теоретической механики Воронежского государственного аграрного университета им. Петра I;
М.Е. Семенов, д-р физ.-мат. наук, проф.
ISBN 978-5-89040-569-2 |
© |
Каверина В.К., 2015 |
|
© |
Воронежский ГАСУ, 2015 |
Введение
Основу теории графов составляет совокупность методов и представлений, которые сформировались при решении конкретных прикладных задач. Во множестве математических объектов графы занимают одно из ведущих мест в качестве основы формирования моделей реальных систем. В рамках теории графов выделяют два основных класса задач. В первом требуется ответить на вопрос, существуют ли графы, обладающие определенным свойством, и если да, то какова оценка их количества. Во втором нужно определить, как построить граф или подграф, обладающий некоторым заданным свойством.
Начало теории графов относят к 1736 году, когда Л. Эйлер решил популярную в то время задачу о кенигсбергских мостах: можно ли совершить прогулку по берегам реки, соединенным семью мостами так, чтобы, выйдя из дома, вернуться обратно, пройдя в точности один раз по каждому мосту?
Однако этот результат более ста лет оставался единственным результатом теории графов. Толчок к развитию теория графов получила в середине XIX века, когда Г. Киркгоф разработал теорию деревьев для исследования электрических цепей, а А. Кэли решил перечислительные задачи для трех типов деревьев.
В настоящее время теория графов стала популярным средством решения задач, связанных с дискретными объектами. К ним, в частности относятся: проектирование и исследование сетей связи, электрических и монтажных схем, программных систем; исследование автоматов, анализ и синтез логических цепей; задачи календарного планирования; поиск информации; разработка стратегий инвестиций; анализ качества, исследование движения транспорта, размещение предприятий коммунального обслуживания, исследование поведения индивидуумов.
Глава 1. Основные понятия
1.1. Формы представления графов. Подграфы. Степени вершин
Определение 1.1. Граф G = ( X ,U ) задан, если даны два конечных множества: а) множество вершин X = {x1 , x2 ,..., xn } ;
б) множество ребер U = {u1 , u2 ,..., um } , состоящее из некоторых пар элементов uk = (xi , x j ) множества вершин X .
Для наглядности геометрически вершинам графа сопоставляют точки, а ребрам – линии, соединяющие некоторые из этих точек.
3

Данное определение графа должно быть дополнено в одном важном отношении. В определении ребра можно принимать или не принимать во внимание порядок расположения двух его концов. Если этот порядок является несущественным, то есть u = (xi , x j ) = (x j , xi ) , то говорят, что ребро
u - неориентированное; если же этот порядок является существенным, то есть, например, xi - начало, а x j - конец ребра, то u называется ориенти-
рованным ребром или дугой.
Определение 1.2. Граф называется неориентированным (неоргра-
фом), если каждое его ребро не ориентировано.
Определение 1.3. Граф называется ориентированным (орграфом),
если каждое его ребро ориентировано, причем xi называется начальной вершиной ребра, а x j - конечной вершиной ребра (xi , x j ) .
Замечания. 1) ориентация ребра указывается стрелкой; 2) говорят, что дуга (xi , x j ) выходит из вершины xi и заходит в вершину x j ; 3) любой неориентированный граф можно трактовать как ориентированный, заменив каждое неориентированное ребро на две дуги, противоположно на-
правленные; 4) граф, имеющий как ориентированные, так и неориентированные ребра, называется смешанным.
Петлей называется ребро (xi , xi ) , у которого начальная и конечная
вершины совпадают. Граф, полученный из орграфа заменой каждой дуги на ребро, называется основанием графа.
Если пара вершин графа соединяется несколькими различными ребрами или дугами, то ребра называются кратными, а их количество – крат- ностью ребра. Граф с кратными ребрами без петель называется мульти- графом. Граф с петлями и кратными ребрами называется псевдографом. Граф без петель и кратных ребер называется простым графом.
Пример 1.1.
x1 |
|
x |
2 |
x |
|
x |
2 |
x |
|
x2 |
x |
|
|
|
|||||||||
|
|
|
1 |
|
|
1 |
|
1 |
|||
|
а) |
|
|
б) |
|
|
в) |
г) |
|||
|
|
|
|
|
Рис. 1.1 |
|
|
|
|||
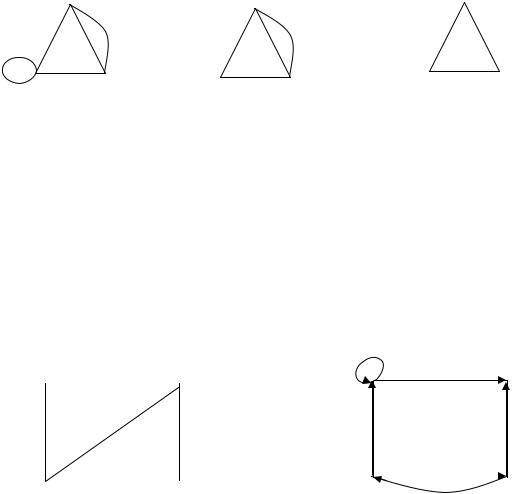
|
На рис. 1.1 а), в) изображены неорграф и смешанный граф соответст- |
||||||||||
венно, у которых кратность ребра (x1 , x2 ) |
равна трем. На рис. 1.1 |
б) изо- |
|||||||||
бражен орграф, у которого кратность ребра (x1 , x2 ) равна двум. На рис. 1.1 г) приведен пример петли (петля обычно считается неориетированной).
Пример 1.2. На рис. 1.2: а) – псевдограф, б) – мультиграф, в) - простой граф.
Определение 1.4. Две вершины графа xi , x j называются смежными, если существует соединяющее их ребро (xi , x j ) , при этом xi , x j называ-
ются концами ребра.
4
x2 |
|
x2 |
|
x2 |
|
x1 |
x3 |
x |
x3 |
x1 |
x3 |
|
|
1 |
|
|
|
|
а) |
|
б) |
|
в) |
|
|
|
Рис 1.2 |
|
|
Определение 1.5. Два ребра смежны, если они имеют общую вершину.
Определение 1.6. Если ребро соединяет вершины xi , x j , то говорят, что ребро инцидентно вершинам xi , x j , а, в свою очередь, вершины xi , x j
инцидентны этому ребру (xi , x j ) .
Вершина, для которой не существует инцидентных ей ребер, называется изолированной. Вершина, для которой существует только одно инцидентное ей ребро, называется висячей.
x 1 |
|
x 2 |
x 1 |
x 2 |
x 4 |
|
x 3 |
x 4 |
|
x 3 |
|
|||||
|
|
||||
|
Рис. 1.3 |
|
|
Рис. 1.4 |
|
Пример 1.3. На рис. 1.3 изображен неориентированный граф, имеющий 4 вершины, 5 ребер. Смежными вершинами являются, например, x1 и x2 , x1 и x4 ; смежными ребрами являются (x1 , x4 ) и (x4 , x2 ) ; ребро (x1 , x2 ) инцидентно вершинам x2 , x1 ; а вершина x3 инцидентна ребрам (x3 , x2 ) и (x4 , x3 ) .
На рис. 1.4 изображен ориентированный граф, имеющий 4 вершины, 6 дуг. Смежными вершинами являются x1 и x2 , x2 и x3 ; смежными дугами являются (x4 , x3 ) и (x3 , x2 ) ; (x3 , x4 ) и (x3 , x2 ) ; дуга (x4 , x3 ) инцидентна вершинам x3 , x4 ; а вершина x4 инцидентна ребрам (x3 , x4 ) , (x4 , x3 ) и (x4 , x1 ) .
Пусть Γ(xi ) - множество вершин x j , для которых в графе G существует ориентированная дуга (xi , x j ) , тогда это множество называется окре- стностью вершины xi . Используя понятие окрестности, граф определяют как совокупность множества вершин и множества окрестностей в виде G = ( X , Γ) , где Γ - неоднозначное отображение, ставящее в соответствие
каждой вершине подмножество Γ(xi ) в X . Γ −1 (xi ) - множество вершин x j , для которых в графе G существует дуга (x j , xi ) . Например, для графа,
5

изображенного на рис. 1.4, множество Γ(x4 ) = {x1 , x3 }, а множество
Γ −1 (x2 ) = {x1 , x3 }.
Если граф ориентированный, то говорят, что дуга (xi , x j ) исходит из вершины xi и заходит в вершину x j . Число дуг, которые имеют вершину xi своей начальной вершиной, называют полустепенью исхода вершины xi
и обозначают d − (xi ) . Число дуг, которые имеют вершину xi своей конечной вершиной, называют полустепенью захода xi и обозначают d + (xi ) . Заметим, что d + (xi ) = Γ −1 (xi ) , d − (xi ) = Γ(xi ) .
Для неориентированного графа G степенью или валентностью вершины xi , называется число ребер, инцидентных вершине xi , то есть число ребер концом которых является вершина xi (при этом петли считаются дважды). Степень вершины xi будем обозначать d (xi ) . Для ориенти-
рованного графа степень вершины xi определяется следующим образом d (xi ) = d − (xi ) + d + (xi ) .
Иначе говоря, степени вершин ориентированного графа есть степени вершин в соответствующем неориентированном графе.
Поскольку каждое ребро инцидентно двум вершинам, в сумму степеней вершин графа каждое ребро вносит двойку. Таким образом, мы приходим к утверждению, которое установлено Эйлером и является исторически первой теоремой теории графов.
Теорема 1.1. Сумма степеней вершин графа G равно удвоенному числу его ребер:
∑ d (xi ) = 2m ,
i
где m - число ребер графа. Изолированная вершина имеет степень 0, висячая вершина – степень 1.
Последовательность d1 ³ ... ³ d n называется графической, если существует граф G на n вершинах x1 ,..., xn такой, что степень d (xi ) вершины xi равна di для любого i . В этом случае d = {d1 ,..., d n } называется после-
довательностью степеней графа или степенной последовательностью.
Рассмотрим графы, обладающие определенными свойствами.
Граф, в котором две любые вершины смежны, называется полным. Полный орграф называется турниром. Этот термин получил свое название
от соревнований по круговой системе, графическое представление которых имеет структуру полного ориентированного графа. В турнирах по круговой системе играют несколько команд, каждая со всеми остальными по одному разу. Игра по правилам не может закончиться в ничью. В представлении графом командам соответствуют вершины, а дуга (x, y) присутствует тогда и только тогда, когда команда x победила команду y . Количество очков команды соответствует числу побежденных ею противников или числу элементов в ее окрестности Γ .
6
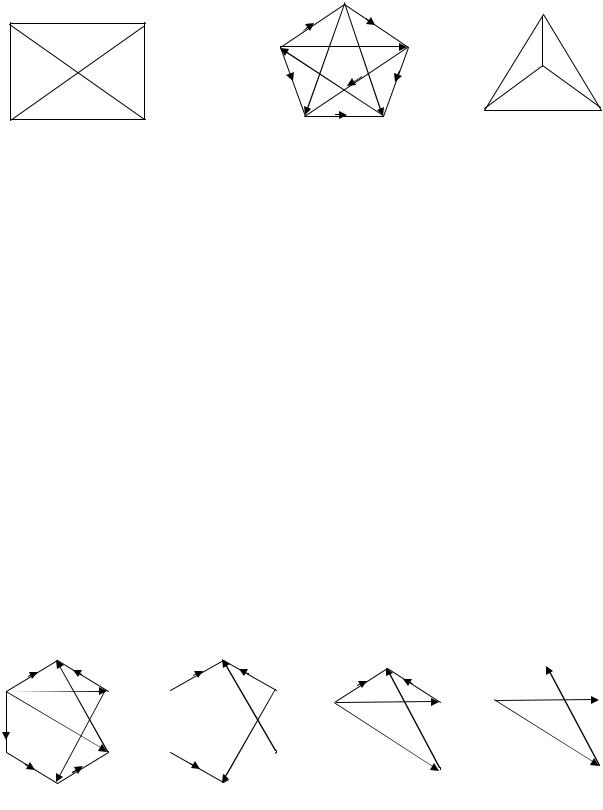
Граф G , который можно изобразить на плоскости так, чтобы ника-
кие два ребра не пересекались в точках, отличных от вершин, называется
планарным графом.
Пример 1.4. На рис. 1.5: а) - полный неорграф, б) - полный орграф, в) – планарный граф.
а) |
|
|
|
б) |
|
в) |
|
Рис. 1.5 |
|
|
|||
В графе можно выделить части – |
подграфы, обладающие некоторы- |
|||||
ми свойствами. Рассмотрим граф G = ( X ,U ) . |
|
|
||||
Определение 1.7. Граф |
G |
′ |
|
′ ′ |
называется |
подграфом графа |
|
= ( X ,U ) |
|||||
G , если X ′ X и U ′ U .
Иначе говоря, от исходного графа остается некоторое подмножество вершин и некоторое подмножество ребер или дуг, соединявших эти вершины.
Определение 1.8. Если X = X ′ , то такой подграф называется остов-
ным.
Примером остовного подграфа может быть подграф Gu = ( X ,U \ u) , полученный из неорграфа G = ( X ,U ) путем удаления ребра u , в дальней-
шем такой подграф будем обозначать сокращенно Gu = G − u . Определение 1.9. Порожденным подграфом графа G на множестве
вершин X |
′ |
называется подграф G |
′ |
|
|
′ ′ |
что U |
′ |
содержит все |
|
|
||||||||||
|
|
|
= ( X ,U ) , такой, |
|
|
|
|||||||||||||||
те ребра из U , которые соединяют вершины из X ′ . |
|
|
|
|
|
|
|
|
|||||||||||||
Определение 1.10. Подграф G′ |
графа G называется максимальным |
|
|
||||||||||||||||||
подграфом по отношению к некоторому свойству P , если G′ обладает |
|
|
|||||||||||||||||||
свойством P и G′ не является подграфом никакого другого подграфа гра- |
|
|
|||||||||||||||||||
фа G , обладающего свойством P . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
x2 |
|
|
|
|
|
|
|
x2 |
|
|
|
x2 |
|
|
|
|
x2 |
|
|
||
x |
|
|
|
x |
|
x |
|
|
|
|
|
x3 |
x1 |
|
x3 |
x1 |
|
|
|
x3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
1 |
|
|
|
|
3 |
1 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
x |
|
|
|
|
|
x4 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x6 |
|
|
|
4 |
x6 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x4 |
|||||||
|
|
|
|
|
|
|
|
|
|
x4 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
x5 |
|
|
|
|
|
|
|
x5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
а) |
|
|
|
|
|
|
|
б) |
|
|
|
в) |
|
|
|
|
г) |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
Рис. 1.6 |
|
|
|
|
|
|
|
|
||
7
Пример 1.5. На рис 1.6 : а) – данный граф, б) – |
остовный подграф, в) |
– порожденный подграф, г) – подграф. |
|
Пример 1.6. Пусть G = ( X ,U ) представляет |
собой карту автомо- |
бильных дорог России: множество вершин X - это города, а множество ребер U - это дороги между городами. Тогда карта всех дорог Воронежской области – это порожденный подграф, а карта всех федеральных трасс России – это остовный подграф.
Задачи и упражнения
1.1. Изобразите графически следующие графы:
а) G1 = ({x1 , x2 , x3 },{(x1 , x2 ), (x1 , x3 ), (x1 , x1 ), (x2 , x3 )}) ;
б) G2 = ({x1 , x2 , x3 , x4 },{(x1 , x2 ), (x1 , x4 ), (x2 , x4 ), (x3 , x3 ), (x3 , x4 ), (x4 , x1 )}) .
1.2. Для графа, изображенного на рис. 1.7, найти:
а) Γ(x2 ) , Γ −1 (x2 ) ; б) d − (x2 ) , d + (x2 ) ;
x1
x5  x2
x2
x4 x3
Рис. 1.7
1.3. Для графа G = ( X ,U ) , изображенного на рис. 1.7, описать: а) описать порожденный подграф G′ , у которого X ′ = {x1 , x2 , x3 , x4 };
′ |
где (xi , x j ) U |
′ |
тогда и только тогда, когда |
б) остовный подграф ( X ,U ) , |
|
||
i + j нечетно. |
|
|
|
1.4. Для неориентированного графа доказать, что число вершин с не- |
|||
четной степенью четно (нуль – |
четное число). |
|
|
1.2. Путь, цепь, контур, цикл. Связность графа
Определение 1.11. Путем в орграфе G называется такая последовательность дуг, в которой конец каждой предыдущей дуги совпадает с на-
чалом следующей. Для неорграфа такая последовательность ребер называется цепью. Под длиной пути (цепи) подразумевается количество дуг (ре-
бер) которые составляют этот путь (цепь).
Определение 1.12. Если каждой дуге (ребру) приписано некоторое число, называемое весом, то граф называется взвешенным.
8

В случае взвешенного графа, длина пути (цепи) – это сумма весов
дуг (ребер), входящих в этот путь.
Определение 1.13. Путь (цепь) называется простым(-ой), если в нем никакая дуга (ребро) не встречается дважды, и составным(-ой) - в про-
тивном случае.
Определение 1.14. Путь (цепь) называется элементарным(-ой), если в нем ни одна вершина не встречается дважды.
Определение 1.15. Путь (цепь), у которого(-ой) начальная и конечная вершина совпадают, называется контуром (циклом).
Пример 1.7.
|
u2 |
x3 |
|
|
u2 |
x3 |
|
|
|
|
|
|
|
u3 |
|||
|
|
|
|
|
|
|||
x2 |
|
u8 |
u3 |
u7 |
|
x4 |
||
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
||
u |
|
u |
7 |
x4 |
|
|
|
|
1 |
|
|
|
|
u6 |
|
|
|
|
u6 |
|
|
u |
|
|
u4 |
|
|
|
u |
|
|
|
|||
x1 |
|
1 |
|
|
|
|
||
|
|
4 |
|
|
|
|
||
u5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x5 |
|
|
x5 |
|
x |
u5 |
|
|||
|
|
|
|
|||||
|
|
|
|
1 |
|
|
|
|
|
|
а) |
|
|
|
б) |
|
|
Рис. 1.8
Для неорграфа, изображенного на рис. 1.8 а):
1)элементарная цепь (x1 , x2 ) , (x2 , x3 ) , (x3 , x4 ) ;
2)элементарный цикл (x1 , x2 ) , (x2 , x3 ) , (x3 , x1 ) ;
3)простая цепь (x1 , x2 ) , (x2 , x3 ) , (x3 , x4 ) , (x4 , x2 ) ;
4)простой цикл (x1 , x2 ) , (x2 , x3 ) , (x3 , x4 ) , (x4 , x2 ) , (x2 , x5 ) , (x5 , x1 ) .
Для орграфа, изображенного на рис. 1.8 б):
1)простой путь (x1 , x2 ) , (x2 , x3 ) , (x3 , x4 ) , (x4 , x5 ) , (x5 , x2 ) ;
2)элементарный контур (x5 , x2 ) , (x2 , x3 ) , (x3 , x4 ) , (x4 , x5 ) .
Ниже приведем без доказательства утверждения, которые будут нам полезны в дальнейшем.
Утверждение 1.1. [3, гл.1, § 4] Объединение двух несовпадающих элементарных цепей, соединяющих вершины xi и x j , содержит цикл.
Утверждение 1.2. [3, гл.1, § 4] Если C и D - два несовпадающих цикла, имеющих общее ребро u , то граф (C D) − u также содержит цикл. (Доказать самостоятельно).
Определение 1.16. Неориентированный граф называется связным, если любые его вершины связаны цепью, иначе граф называется несвяз-
ным.
Для орграфов понятие связности является более содержательным. Можно выделить три типа связности орграфа.
9
Определение 1.17. Орграф называется слабо связным, если его основание есть связный граф; односторонне связным, если для любых двух
различных вершин xi и x j существует, по крайней мере, один путь из xi в x j , или из x j в xi ; сильно связным, если для любых двух различных вершин xi и x j существует путь из xi в x j и обратно.
Определение 1.18. Всякий максимальный связный подграф графа G
называется компонентой связности графа G или связной компонентой.
Еще раз напомним, что слово «максимальный» означает максимальный относительно включения, то есть не содержащийся в связном подграфе с бόльшим числом элементов.
Аналогично, для орграфа формулируется понятие односторонней компоненты связности, сильной компоненты связности.
Пример 1.8. На рис 1.9: а) – связный неорграф, б) – несвязный неорграф, содержащий две компоненты связности, в) – сильно связный орграф.
x |
|
|
|
x 2 |
x 4 |
x 2 |
|
x 4 |
2 |
|
x 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 4 |
|
|
|
|
|
x 1 |
|
|
|
|
|
|
|
x 5 |
|
x 5 |
|
x |
x |
3 |
|||
|
|
x 3 |
1 |
|||||
|
|
|
x 1 |
x 5 |
|
|
||
|
|
|
|
|
|
|||
|
|
а) |
б) |
|
в) |
|
|
|
|
|
|
|
Рис. 1.9 |
|
|
|
|
|
|
Теорема 1.2. [3, гл.1, § 4] Каждый граф представляется в виде объе- |
||||||
динения своих связных компонент. Разложение графа на связные компоненты определено однозначно.
Отметим, что указанная теорема позволяет сводить большинство задач, касающихся графов, к случаю связных графов. Полезна также и следующая
Лемма 1.1. [3, гл.1, § 4] Пусть G = ( X ,U ) - связный граф. Тогда:
1) если ребро u U принадлежит какому-либо циклу графа G , то граф G − u связен;
2) если ребро u U не входит ни в какой цикл, то граф G − u имеет ровно две компоненты связности.
На вопрос, сколько ребер может быть в графе с n вершинами и фиксированным числом компонент связности k отвечает следующая
Теорема 1.3. [3, гл.1, § 4] Пусть число компонент связности простого графа G = ( X ,U ) равно k , число ребер m , число вершин n . Тогда справедлива следующая оценка
n − k ≤ m ≤ (n − k )(n − k + 1) , 2
причем обе эти оценки для m достижимы.
10
