Учебное пособие 985

Постановка задачи. Пусть дан орграф G = ( X ,U ) . Требуется найти

все гамильтоновы контуры данного графа.

Алгебраический метод выделения гамильтоновых путей и контуров

Шаг 1. Положить k = 1, Pk = A .

Шаг 2. Положить k = k + 1 и найти Pk = B ´ Pk −1 .

Шаг 3. Если k = n , то диагональные элементы матрицы Pk дают внутренние произведения вершин, которые соответствуют гамильтоновым контурам графа. Получить гамильтоновы контуры.

Иначе перейти к шагу 4.

Шаг 4. Сделать все цепи простыми, обнулив в матрице Pk все диагональные элементы, которые содержат сомножителями вершины, соответствующие данной строке. Перейти к шагу 5.

Шаг 5. Если k = n − 1, то элементы матрицы Pk дают внутренние произведения вершин, которые соответствуют данным гамильтоновым путям графа G . Получить гамильтоновы пути.

Иначе перейти к шагу 2.

Еще раз подчеркнем, что построенная матрица Pn−1 дает все гамильтоновы пути, имеющие длину n − 1, между всеми парами вершин. Поэтому гамильтоновы контуры можно получать сразу из путей в Pn−1 и тех дуг из G , которые соединяют начальную и конечную вершины каждого контура. С другой стороны, гамильтоновы контуры даются членами внутреннего произведения вершин, стоящими в любой диагональной ячейке матрицы B × Pn−1 (все диагональные элементы этой матрицы дают одинаковые контуры).

Рис. 1.18

Пример 1.15. Рассмотрим граф G изображенный на рис. 1.18, матрица смежности и модифицированная матрица смежности которого равны

21

22

Гамильтоновы пути abdce и adcbe , соответствующие элементу (1,5) матрицы P4 , дают гамильтоновы контуры abdcea и adcbea , если добавить дугу (e, a) . Все другие гамильтоновы пути приводят к тем же самым гамильтоновым путям, и поэтому в графе G существуют только эти два контура. (Самостоятельно найдите матрицу P5 и убедитесь, что ее диагональные элементы дают те же контуры).

Задачи и упражнения

1.11. Существует ли эйлеров цикл в графах, изображенных на рис.

1.19?

Рис. 1.19

1.12. Определить (если существуют) гамильтоновы пути и контуры алгебраическим методом в графах, изображенных на рис. 1.20?

Рис.1.20

1.13. Задача Эйлера о шахматном коне [9]. Найдите такую последователь-

ность ходов шахматного коня, чтобы, начав с произвольной клетки, пройти через каждую клетку шахматной доски один раз и вернуться в исходную.

1.6. Основные числа теории графов

Число внутренней устойчивости

Определение 1.26. Множество вершин графа называется внутренне устойчивым (независимым), если никакие две вершины этого множества

не смежны.

23

Определение 1.27. Внутренне устойчивое множество называется максимальным, если его нельзя пополнить ни одним элементом без нару-

шения свойства внутренней устойчивости. Наибольшее по мощности внутренне устойчивое множество называется наибольшим.

Ясно, что наибольшее внутренне устойчивое множество является максимальным. Обратное, вообще говоря, неверно.

Пример 1.16. Для графа, изображенного на рис. 1.21, множество вершин {5,8} является внутренне устойчивым, {4,7} – максимальным внутренне устойчивым множеством, не являющимся наибольшим, а множества {1,2,3,7}, {2,3,5,8} – наибольшими внутренне устойчивыми множествами.

Рис. 1.21

Определение 1.28. Число элементов в наибольшем внутренне устойчивом множестве графа G = ( X ,U ) называется числом внутренней устой-

чивости и обозначается .

Для графа из примера 1.15 число внутренней устойчивости α (G) = 4 . К отысканию числа внутренней устойчивости графа сводится, например, известная задача о восьми ферзях, которую связывают с именем

немецкого математика К. Гаусса.

Пример 1.16. (Задача о восьми ферзях.) Чему равно наибольшее количество ферзей, которых можно расставить на шахматной доске так, чтобы ни один ферзь не находился под ударом?

Таких ферзей, очевидно, не может быть более восьми, так как никакие два из них не должны находиться на одной вертикали или горизонтали. Рассмотрим граф, вершины которого соответствуют клеткам доски, а ребра – парам клеток, лежащих на одной вертикали, горизонтали или диагонали. Ясно, что расстановке ферзей соответствует наибольшее внутренне устойчивое множество. Наибольшее количество ферзей, которых можно расставить на шахматной доске так, чтобы ни один ферзь не находился под ударом, равно числу внутренней устойчивости α (G) = 8 , один из вариантов расстановки ферзей можно найти в [3, гл. IV, § 25].

Множества внутренней устойчивости вершин графа имеют различные применения. Одно из них связано с задачей кодирования в теории ин-

формации ([9, гл. 13, п. 13.3].).

24

Число внешней устойчивости

Определение 1.28. Пусть дан граф G = ( X ,U ) . Подмножество вер-

шин графа A X называется внешне устойчивым (доминирующим), если каждая вершина из A = X \ A смежна с некоторой вершиной из A .

Определение 1.29. Внешне устойчивое множество называется мини- мальным, если из него нельзя удалить ни один элемент без нарушения

свойства внешней устойчивости. Внешне устойчивое множество, имеющее наименьшую мощность, называется наименьшим.

Определение 1.30. Число элементов в минимальном по мощности внешне устойчивом множестве графа G = ( X ,U ) называется числом внеш-

ней устойчивости и обозначается β (G) .

Пример 1.17. Схема тюрьмы представлена в виде графа (рис. 1.22): вершины – посты караула, ребра – коридоры, куда выходят двери камер. Какое наименьшее количество охранников требуется, чтобы они видели все посты?

5

Рис. 1.22

Очевидно, что число внешней устойчивости является минимальным числом охранников, необходимых для решения этой задачи. Для этого графа β (G) = 2. В качестве постов, с которых просматриваются все остальные посты, можно взять, например, множество вершин {2,5}, которое является наименьшим внешне устойчивым множеством.

Пример 1.18. (Задача о пяти ферзях.) Чему равно наименьшее количество ферзей, которых можно расставить на шахматной доске так, чтобы каждая клетка доски находилась под ударом?

Рассмотрим граф, вершины которого соответствуют клеткам доски, а ребра – парам клеток, лежащих на одной вертикали, горизонтали или диагонали. Ясно, что расстановке ферзей соответствует наименьшее внешне устойчивое множество. Наименьшее количество ферзей, которых можно расставить на шахматной доске так, чтобы каждая клетка доски находи-

25

лась под ударом, равно числу внешней устойчивости β (G) = 5 , один из вариантов расстановки ферзей можно найти в [3, гл. IV, § 25].

Отыскание в графе минимального внешне устойчивого множества с наименьшим количеством элементов является сутью многих прикладных задач. Например, пусть имеется множество населенных пунктов, связанных сетью дорог. В некоторых из них надо разместить предприятия обслуживания так, чтобы расстояние от каждого из населенных пунктов до какого-либо из предприятий не превосходило заданной величины. Размещение следует выполнить так, чтобы обойтись минимальным количество предприятий. Если поставить в соответствие населенным пунктам вершины графа, в котором две вершины смежны тогда и только тогда, когда расстояние между соответствующими пунктами не превышает заданной величины, то задача, очевидно, сводится к построению в графе наименьшего внешне устойчивого множества.

Ядро графа

Определение 1.30. Пусть дан граф G = ( X ,U ) . Подмножество вершин графа S X называется ядром, если оно одновременно внутренне и внешне устойчиво.

Существуют графы, у которых нет ядра, а также графы с несколькими ядрами. Например, для графа, изображенного на рис. 1.21, множества вершин {1,2,3,7}, {1,2,3,8}, {2,3,5,7}, {2,3,5,8}, {4,7} являются ядрами гра-

фа.

Теорема 1.9. (Необходимое условие существования ядра в графе.)

Для того, чтобы в графе существовало ядро необходимо, чтобы

α (G) = β (G) .

Понятия внутренне, внешне устойчивого множества, ядра естественным образом переносятся на случай ориентированных графов в [3, гл. X, § 67].

Хроматическое число графа

Определение 1.31. Граф G = ( X ,U ) , ориентированный или неориентированный, называется r-раскрашиваемым, если его вершины могут быть окрашены в r цветов так, что никакие две смежные вершины не будут окрашены в один цвет. Такая раскраска графа называется правильной.

Определение 1.32. Минимальное число r, при котором граф являет-

ется r-хроматическим. Такая раскраска графа называется минимальной. Для некоторых графов найти хроматические числа несложно. На-

пример, граф является 1-хроматическим тогда и только тогда, когда он пустой (не содержит ребер). Полный граф на n вершинах имеет хроматиче-

26

ское число n. Обычно 2-хроматический граф называют бихроматическим. Справедлива

Теорема 1.10. (Теорема Кенига.) Непустой граф является бихроматическим тогда и только тогда, когда он не содержит циклов нечетной длины.

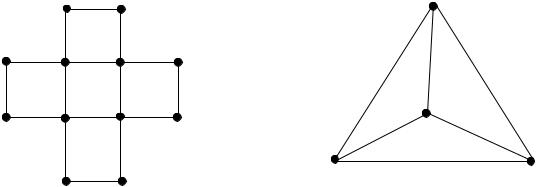
Пример 1.19. На рис. 1.23: а) – бихроматический граф, б) - 4-хроматический граф.

Рис 1.23

Задачи отыскания хроматического числа и построения минимальной раскраски произвольного графа являются очень сложными, эффективные алгоритмы их решения неизвестны. Рассмотрим простой алгоритм построения правильной раскраски графа, в ряде случаев приводящий к раскраскам, близким к минимальным.

Алгоритм раскраски

Шаг 1. Найдем степени вершин графа.

Шаг 2. Расположим все вершины графа в порядке невозрастания их степеней.

Шаг 3. В первый цвет окрашиваем первую вершины из списка, и двигаясь вдоль списка, в этот же цвет окрашиваем каждую вершину не смежную с уже окрашенными до нее в этот цвет.

Шаг 4. Берем первую из неокрашенных вершин, двигаясь вдоль списка, и окрашиваем в другой цвет саму вершину и все не смежные с уже окрашенными в этот цвет и т.д.

Пример 1.20. Построить правильную раскраску графа, изображенного на рис. 1.24.

Шаг 1. Найдем степени вершин графа: d (x1 ) = 4 , d (x2 ) = 3 , d (x3 ) = 4 ,

d (x4 ) = 4 , d (x5 ) = 3 , d (x6 ) = 3 , d (x7 ) = 3 .

27

Шаг 2. Расположим вершины в порядке невозрастания степеней их вершин:

Шаг 3. Окрасим вершину x1 в цвет А, затем в этот же цвет окрашиваем каждую вершину не смежную с уже окрашенными до нее в этот цвет. Такая вершина одна - x4 .

Шаг 4. Берем первую из неокрашенных вершин – это вершина x3 , окрашиваем ее в цвет B, двигаясь вдоль списка, окрашиваем и не смежные с уже окрашенными в этот цвет вершины – это вершина x5 .

Берем первую из неокрашенных вершин – это вершина x2 , окрашиваем ее в цвет C, двигаясь вдоль списка, окрашиваем все не смежные с уже окрашенными в этот цвет вершины – это вершины x6 , x7 .

Граф является 3-раскрашиваемым. Раскраска является правильной. Для наглядности расставим полученные при раскраске цвета рядом с вершинами графа. Так как граф содержит циклы нечетной длины, то согласно

хроматическим.

Рассмотрим некоторые практические задачи, сводящиеся к правиль-

ной раскраске графа.

1. Задача составления расписаний. Предположим, что нужно про-

честь несколько лекций за кратчайшее время. Чтение каждой лекции в отдельности занимает один час, но некоторые лекции не могут читаться одновременно (например, их ведет один и тот же лектор). Построим граф,

28

вершины которого соответствуют лекциям, две вершины смежны тогда и только тогда, когда соответствующие лекции нельзя читать одновременно. Очевидно, что любая правильная раскраска этого графа определяет допустимое расписание: лекции, окрашенные в один цвет, могут читаться одновременно. Оптимальные расписания соответствуют минимальным раскраскам, а число часов, необходимое для прочтения лекций, равно γ (G) .

2. Задача распределения оборудования. Пусть необходимо выпол-

нить n работ. Известно, что для выполнения каждой из работ требуется некоторое время, одинаковое для всех работ, и некоторые механизмы. При этом никакой из механизмов не может быть одновременно занят в нескольких работах. Нужно распределить механизмы так, чтобы общее время выполнения всех работ было минимальным.

Построим граф, вершины которого соответствуют выполняемым работам. Соединим ребром любую пару вершин, если для выполнения соответствующих работ требуется хотя бы один общий механизм. При правильной раскраске графа работы, соответствующие вершинам одного цвета, можно выполнять одновременно, а наименьшее время выполнения всех работ достигается при минимальной раскраске и равно γ (G) .

Проблема четырех красок

Проблема раскраски планарных графов является одной из самых знаменитых проблем теории графов. Возникшая в середине 19 века, она до сих пор привлекает внимание специалистов.

Первоначально вопрос формулировался так: достаточно ли четырех красок для такой раскраски произвольной географической карты, при которой любые две соседние страны окрашены в различные цвета? При этом рассматриваются те карты, в которых граница любой страны состоит из одной замкнутой линии, а соседними считаются страны, имеющие общую границу ненулевой длины.

В 1879 году британский математик А. Кэли опубликовал статью, в

которой сформулировал гипотезу четырех красок: всякая карта 4- раскрашиваема. Часто пользуются другой формулировкой гипотезы: вся-

кий планарный граф 4-раскрашиваем.

Первоначально гипотеза четырех красок не показалась сложной и появилось несколько ее доказательств, в которых позднее были обнаружены пробелы. В дальнейшем эту проблему пытались решить многие известные математики. Большой интерес к гипотезе способствовал открытию многих важных результатов в теории графов. До сих пор эта проблема остается мощным стимулом исследования различных свойств графов.

Цикломатическое число графа

29

Пусть G = ( X ,U ) - связный граф. Обозначим число ребер этого гра-

фа через m , число вершин - n . Тогда число

ν (G) = m - n +1

называют цикломатическим числом графа G.

Теорема 1.10. Для любого связного графа G цикломатическое число удовлетворяет неравенству

ν (G) ³ 0 .

Причем ν (G) = 0 тогда и только тогда, когда G является деревом, и ν (G) = 1 тогда и только тогда, когда G содержит единственный цикл.

В общем случае, когда число компонент связности графа G равно p , цикломатическое число находится по формуле

ν (G) = m - n + p .

Очевидно, что граф G не содержит циклов тогда и только тогда, когда ν (G) = 0 .

Задачи и упражнения

1.14. Для графа, изображенного на рис. 1.25 укажите внутренне устойчивое, максимальное внутренне устойчивое, наибольшее внутренне устойчивое множества; внешне устойчивое, минимальное внешне устойчивое, наименьшее внешне устойчивое множества. Найдите число внутренней устойчивости, число внешней устойчивости, хроматическое и цикломатическое число. Постройте правильную раскраску.

Рис. 1.25

30