Учебное пособие 985

Χ(R*, R*) = r(R*, R*) и Χ(R*, R*) = 0 .

Вычтем из первого уравнения второе

Χ(R*, R*) − Χ(R*, R*) = r(R*, R*) .

В силу равенства (2.5)

v* = r(R*, R*) ,

то есть величина максимального потока равна пропускной способности построенного разреза.

Так как v* ≤ r(R, R ) , то

v* = r(R*, R*) ≤ r(R, R ) для любого разреза R . Следовательно, разрез R * - минимальный разрез.

2.2.2. Алгоритм Форда-Фалкерсона

Постановка задачи. Задача о максимальном потоке заключается в нахождении такого потока в сети, чтобы величина потока v была максимальной.

Метод решения задачи о нахождении максимального потока в сети.

Решение задачи основано на теореме Форда-Фалкерсона. Условия задачи могут быть изображены в виде ориентированного графа с двумя выделенными вершинами s и t , на каждой дуге которого записано некоторое положительное число – пропускная способность этой дуги.

Итог решения задачи: это тот же граф, но на каждой дуге теперь (через запятую после величины пропускной способности) полученное значение xij ³ 0 - потока на этой дуге. В ответ так же входит величина макси-

мального потока v * и выписанное отдельно множество дуг (R*, R*) , представляющее минимальный разрез.

Метод решения – специальный алгоритм расстановки пометок при вершинах графа. Чтобы избежать многократного перерисовывания сети, применяют особый способ записи. Начальный поток на сети считают нулевым, то есть полагают все xij равными нулю.

Алгоритм решения задачи о максимальном потоке и минимальном разрезе

Расстановка пометок. Вершина может находиться в одном из трех состояний:

-вершине приписана пометка, и она просмотрена (т.е. она имеет пометку и все смежные вершины "обработаны");

-вершина имеет пометку, но не просмотрена (т.е. не все смежные с ней вершины "обработаны");

-вершина не имеет пометки.

Пометка произвольной вершины xi состоит из двух частей и имеет один из двух видов: (+x j ,δ ) или (-x j ,δ ) . Часть + x j пометки первого ти-

41

па означает, что поток допускает увеличение вдоль дуги (x j , xi ) . Часть

полнительного потока, который может протекать по некоторому пути от s к xi

Шаг 1. Вершина s помечается специальной пометкой (+s, ∞) . Вершине s присвоена пометка, все остальные вершины без пометок.

Шаг 2. Выбрать непросмотренную вершину с пометкой (± xk ,θi ) .

а) каждой непомеченной вершине x j Γ(xi ) , для которой xij < rij присвоить пометку (+ xi ,θ j ) , где θ j = min{θi , rij − xij };

б) каждой непомеченной вершине x j Γ −1 (xi ) , для которой x ji > 0 присвоить пометку (−xi ,θ j ) , где θ j = min{θi , x ji }.

Теперь вершина xi и помечена, и просмотрена, а вершины x j , пометки которым присвоены в а) и б), являются непросмотренными.

Шаг 3. Повторять шаг 2 до тех пор, пока либо вершина t не будет помечена, и тогда перейти к шагу 4, либо t будет не помечена и никаких других пометок нельзя будет расставить. Если при этом R * - множество помеченных вершин, а R * - множество непомеченных вершин, то (R*, R*) - минимальный разрез, а сумме пропускных способностей на дугах этого разреза есть величина максимального потока v *.

Увеличение потока.

Шаг 4. Пусть вершина t имеет пометку (± y,θt ) , тогда положить x = t и перейти к шагу 5.

Шаг 5. а) если пометка в вершине x имеет вид (+ z,θ x ) , то увеличить поток вдоль дуги (z, x) на величину θt .

б) если пометка в вершине x имеет вид (−z,θ x ) , то уменьшить поток вдоль дуги (x, z) на величину θt .

Перейти к шагу 6.

Шаг 6. Если z = s , то стереть все пометки и вернуться к шагу 1, иначе положить x = z и вернуться к шагу 5.

Замечание. После завершения работы алгоритма целесообразно проверить: 1) Все ли дуги, входящие в минимальный разрез, насыщены потоком, т.е. выполняется ли условие xij * = rij для любой дуги

(xi , x j ) (R*, R*) . Если хотя бы для одной дуги этого разреза условия насыщенности нарушено, то задача решена неверно; 2) Кроме того, необходимо убедиться, что сумма всех потоков, выходящих из s , равна v * и совпадает с суммой всех потоков, входящих в t .

Пример 2.2. Найти максимальный поток и минимальный разрез в сети, изображенной на рис. 2.4.

Возьмем в качестве начального потока - поток с нулевыми значениями на всех дугах. Запишем все вершины в первый столбец таблицы 2.2, на-

42

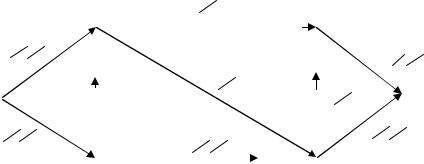
чиная с s по t . Каждый отчеркнутый столбик соответствует циклу расстановки пометок. Все столбики, кроме последнего, содержат пометку вершины t , в последнем эта пометка не появляется. Именно вершины, помеченные в последнем столбике, и образуют множество R *. Величины потоков на дугах последовательно нарастают, при этом предыдущие меньшие значения зачеркиваются. Последние полученные цифры и есть максимальные потоки на дугах.

Рис. 2.4

вершине x2 приписывается пометка (+s, min[∞,10 − 0]) , то есть (+s,10) .

б) Множество вершин {x j : x j Γ −1 (s), x js > 0, x j − не помечена} является пустым. Итак, s помечена и просмотрена, x1 и x2 помечены и не просмотрены, а все остальные вершины не помечены. Повторяем шаг 2 и первой просматриваем вершину x1 .

а) Множество вершин

{x j : x j Γ(x1 ), x1 j < r1 j , x j − не помечена}= {x3 , x4 }, вершине x3 приписывается пометка (+ x1 , min[8,3 − 0]) , то есть (+ x1 ,3) , вершине x4 приписывается пометка (+x1 , min[8,4 − 0]) , то есть (+x1 ,4) .

43

б) Множество вершин {x j : x j Γ −1 (x1 ), x js > 0, x j − не помечена} является пустым. Итак, s и x1 помечены и просмотрены, а x2 , x3 , x4 помечены и не просмотрены, а все остальные вершины не помечены.

Беря для просмотра вершину x2 , найдем, что никаких пометок расставить нельзя.

Беря для просмотра вершину x4 и повторяя шаг 2, придем к следующим пометкам:

для t пометкой будет (+x4 , min[4,8 − 0]) , то есть (+x4 ,4) .

Вершина t помечена, заносим все полученные пометки во второй столбец таблицы 2.2, и переходим к шагам 4 и 5 алгоритма. В результате получим:

x = t ; x4t = 0 + 4 = 4 ; x = x4 ; x14 = 0 + 4 = 4 ; x = x1 ; xs1 = 0 + 4 = 4 .

Там где значение потока на дугах сети изменилось - зачеркиваем старые значения потока, и указываем новые. Возвращаясь к шагу 1 для второго прохода, получим новые пометки вершин, которые мы занесем в третий столбец таблицы 2.2,

Пометкой для s будет (+s, ∞) ,

пометкой для x1 будет (+s, min[∞,8 − 4]) = (+s,4) ,

пометкой для x2 будет (+s, min[∞,10 − 0]) = (+s,10) ,

теперь вершина s помечена и просмотрена.

Пометкой для x3 будет (+x1 , min[4,3 − 0]) = (+x1 ,3) ,

теперь вершина x1 помечена и просмотрена.

Пометкой для x4 будет (+x2 , min[10,5 − 0]) = (+ x2 ,5) ,

теперь вершина x2 помечена и просмотрена.

Пометкой для t будет (+x4 , min[5,8 − 4]) = (+x4 ,4) ,

Вершина t помечена, переходим к шагам 4 и 5 алгоритма. В результате получим:

x = t ; x4t = 4 + 4 = 8 ; x = x4 ; x24 = 0 + 4 = 4 ; x = x2 ; xs 2 = 0 + 4 = 4 .

Продолжая дальше, получаем после каждого прохода алгоритма поток и пометки, которые записываем на дугах сети и заносим в столбцы таблицы 2.2. Алгоритм заканчивает работу, когда вершина t не может быть помечена.

Обозначим множество всех помеченных вершин на последнем шаге через R * и соответственно R* = X \ R * :

R* = {s, x1 , x2 }, R* = {x3 , x4 , t},

(R*, R*) = {(x1 , x3 ), (x1 , x4 ), (x2 , x4 )}.

44

Все дуги, входящие в разрез (R*, R*) , насыщены потоком. Пропускная способность найденного минимального разреза равна: v* = 3 + 4 + 5 = 12 .

Проверим: из s выходит 7 + 5 = 12 единиц потока, а в t входит 7 + 5 = 12 единиц потока.

Задачи и упражнения

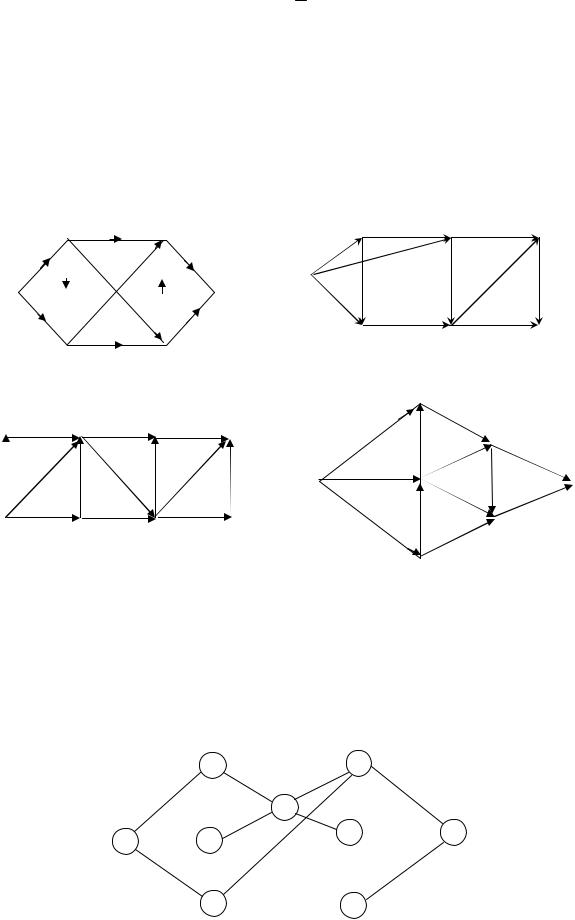
2.3. Найти максимальный поток и минимальный разрез для графов, изображенных на рис. 2.5.

ниченное число туристских групп. На рис.2.6 на каждой дуге (ai , ak ) около узла ai указано максимальное число (за один день) групп, которые

Рис. 2.6

45

Глава 3. Задача сетевого планирования

3.1.Сетевая модель комплекса работ

Внастоящее время в связи с осуществлением крупномасштабных технических проектов, строительством современных предприятий, выполнением сложных научных разработок постоянно приходится решать задачи рационального планирования большого комплекса работ. Например, строительство промышленного объекта включает в себя создание подъездных путей и энергетических коммуникаций, подготовку строительной техники, подвоз материалов, возведение фундаментов и корпусов, выполнение отделочных работ, установку и отладку оборудования, а также исполнения других необходимых работ и операций. При этом возникает вопрос об очередности проведения работ, о распределении людей и материальных ресурсов, о времени, необходимом для выполнения всего проекта в целом.

Все упомянутые и многие другие ситуации имеют некоторые общие черты, которые мы выделим:

1) вся работа представляет собой комплекс более мелких звеньев, элементарных работ (например, в случае строительства – это могут быть подвоз материалов, рытье котлована и т.д.);

2) работы друг друга обусловливают, т.е. не могут выполняться в произвольном порядке. Для начала одних работ требуется предварительное выполнение некоторых других работ.

Обычными параметрами, которыми интересуются в приведенных ситуациях, являются:

1.Время, необходимое на выполнение, как всего комплекса работ, так и отдельных звеньев.

2.Стоимость работ всего комплекса и отдельных звеньев.

3.Ресурсы, необходимые для выполнения работ.

При этом возникает задача рационального планирования работ. Для решения поставленных проблем используются методы сетевого планирования, которые предполагают построение сетевой модели всего комплекса работ. Сетевая модель изображается в виде сетевого графика, отображающего технологическую взаимосвязь между работами.

Определение 3.1. Ориентированный граф, в котором существует лишь одна точка A0 , не имеющая входящих вершин, и лишь одна точка An

не имеющая выходящих дуг, каждой дуге которого приписано некоторое число, называется сетевым графиком.

Определение 3.2. Путь сетевого графика называется полным, если его начало совпадает с вершиной A0 , а конец с вершиной An .

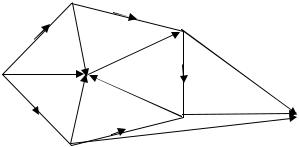
Как правило, сетевой график имеет большое число полных путей. Пример 3.1. На рис. 3.1 изображен сетевой график, полными для не-

го являются пути, проходящие через вершины A0 , A2 , A3 , A6 , длина пути равна 10; A0 , A1 , A3 , A6 , длина пути равна 9 и т.д.

46

Рис. 3.1

Всетевом планировании основные элементы сетевого графика (дуги

ивершины) принято называть соответственно работами и событиями:

Термин работа может иметь различные значения:

-действительная работа, требующая затрат времени и ресурсов;

-ожидание – процесс, не требующий затрат труда, но занимающий

время (например, твердение бетона); - фиктивная работа – логическая связь между двумя или несколь-

кими работами (событиями), не требующая затрат труда и времени. Она указывает, что возможность начала одной работы непосредственно зависит

от результата другой. Продолжительность фиктивной работы равна нулю. Событие – это момент завершения какого-либо процесса. Событие

может являться частным результатом отдельной работы или суммарным результатом нескольких работ. Конечный результат любой работы важен не только как факт окончания данной работы, но и как необходимое условие для начала следующих работ. Событие может свершиться только тогда, когда закончатся все работы, ему предшествующие. Последующие работы могут начаться только тогда, когда событие свершится. Событие не имеет продолжительности во времени. Свершение события есть момент времени, соответствующий моменту окончания последней из работ, непо-

средственно предшествующих ему.

Сетевой график ограничен исходным и завершающим событиями.

Исходное событие не имеет предшествующих работ и событий и пред-

ставляет собой формулировку условия для начала работ по выполнению комплекса работ. Завершающее событие не имеет последующих работ и

событий и представляет собой формулировку конечной цели комплекса работ.

У всех событий сети, кроме исходного и завершающего, имеются, по крайней мере, по одной непосредственно предшествующей и по одной не-

посредственно за ним следующей работе. Событие, непосредственно предшествующее работе, по отношению к ней называется начальным, а событие, непосредственно следующее за ней, - конечным.

Виды сетевых моделей зависят от различной интерпретации дуг и вершин графа. Существует два способа отображения сетевых моделей в зависимости от того, что будут изображать дуги и вершины – работы или события:

47

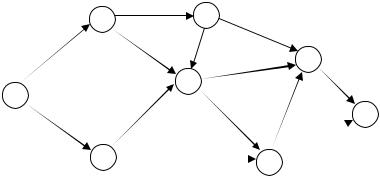
1) сетевые модели в терминах событий – наиболее распространен-

ный способ изображения сетей; события изображаются вершинами, а ра-

боты - дугами графа; 2) сетевые модели в терминах работ: в этом случае работы изобра-

жаются вершинами графа, а дуги показывают взаимосвязь отдельных работ.

В дальнейшем мы будем пользоваться только первым способом изображения сетевой модели.

Исходная информация о работах, которые требуется выполнить, должна содержать перечень всех работ, последовательность их выполнения и оценку каждой работы (продолжительность, стоимость и т.п.). Так,

например, информация о некотором проекте может быть задана в виде структурной таблицы комплекса работ (таблица 3.1).

Сетевой график в терминах событий строится следующим образом: кружками обозначаются события; стрелками, соединяющими события, обозначаются работы. Сплошными стрелками изображаются действительные работы, пунктирными – ожидания и фиктивные работы.

Рис. 3.2

Построим сетевой график для последовательности работ, представленной в таблице 3.1. На предварительном этапе события, обозначающие

48

начала или концы работ, можно нумеровать в произвольном порядке. Пусть 0 - исходное событие. Работы a1 и a2 не имеют предшествующих работ, поэтому они выходят из исходного события. В конце дуг, соответствующих работам a1 и a2 изображаются события, характеризующие окончание этих работ. Обозначим их, например, 1 и 2. Работы a3 и a4 опираются на работу a1 , следовательно, из события 1 выходят две дуги, отвечающие работам a3 и a4 . Концами этих работ служат события 6 и 3 соответственно. Работы a5 и a6 опираются на работу a2 , следовательно, из события 2 выходят две дуги, отвечающие работам a5 и a6 . Событие, являющееся концом работы a5 , можно объединить с событием 3, так как последующие работы a9 и a10 , как видно из структурной таблицы, обе опираются на работы a4 и a5 . Событие 5 означает завершение работы a6 . Указанный процесс продолжается до тех пор, пока не будут построены все работы. На работы a12 и a13 не опирается ни одна работа, поэтому их окончанием служит завершающее событие 7. Сетевой график изображен на рис. 3.2. Он выражает логическую связь в последовательности событий и работ.

3.2. Правила построения сетевого графика

При построении сетевого графика следует соблюдать ряд правил, которые позволяют также проверить правильность его построения.

1. В сети не должно быть событий (кроме завершающего), из которых не выходит ни одна работа. Наличие таких «тупиковых» событий указывает на то, что забыта какая-нибудь работа, которая должна выполняться после этого события, либо предшествующая ему работа не нужна для за-

вершения всего комплекса работ. Если имеется несколько завершающих событий, то их следует соединить в одно новое завершающее событие фиктивными работами нулевой продолжительности.

2.В сети не должно быть событий (кроме исходного), в которые не входит ни одна работа. Если имеется несколько исходных событий, то они соединяются с одним, вновь введенным исходным событием, фиктивными работами нулевой продолжительности.

3.В сети не должно быть контуров. Это следует из того, что каждая работа, входящая в событие, предшествует работе, из него выходящей.

4.Нельзя допускать, чтобы у двух или более выполняемых парал-

лельно во времени работ совпадали и начальное и конечное события. Такие работы должны завершаться самостоятельными событиями, которые далее соединяются с одним (для данной группы работ) событием фик- тивными работами.

На рис. 3.3 а) и 3.3 б) приведены соответственно неправильный и правильный способы представления фрагмента сетевого графика.

5. Если для начала какой-либо работы необходимо завершение всех работ, входящих в предшествующее этой работе событие, а для другой,

49

начинающейся этим же событием, - только части из них, то данное событие разбивается на два, связанных фиктивной работой. В первое из них входят работы, частный результат которых достаточен для начала одной работ, а во второе – остальные.

2

1 3 4

Рис. 3.3

3.3. Упорядочение сетевого графика

Для удобства работы с сетью по определению временных параметров

целесообразно произвести упорядоченную нумерацию событий. Под се-

тью, с упорядоченной нумерацией событий, понимают такую сеть, в кото-

рой для каждой работы номер ее начального события меньше номера ее конечного события. Упорядочение сети можно осуществить с помощью матрицы смежности (см. определение 1.19). Номерами строк и столбцов этой матрицы являются номера событий. Упорядочение сети с помощью матрицы смежности рассмотрим на примере сетевого графика, представленного на рис. 3.2. Матрица смежности для этой сети приведена в таблице 3.2 (нулевые элементы матрицы смежности могут не проставляться).

Обозначим через v0 , v1 , v2 , …, v7 векторы, являющиеся строками матрицы смежности. Найдем компоненты нового вектора V0 по формуле

и припишем их снизу к матрице смежности, в качестве первой дополнительной строки. Отметим, что i -ая компонента вектора V0 равна числу работ, заканчивающихся i -ым событием. Так как событию 0 соответствует компонента, равная нулю, то это событие является исходным и образует нулевой слой. Исключим из дальнейшего рассмотрения событие 0 и работы с началом в этом событии, т.е. исключим вектор v0 . Вычислим компоненты вектора по формуле

= − R

V1 V0 v0

и запишем их во второй дополнительной строке таблицы 3.1. Здесь появилось еще два нуля, соответствующих событиям 1 и 2. Эти нули свидетель-

ствуют о том, что данные события не имеют предшествующих в сетевом графике без события 0. Следовательно, события 1 и 2 образуют первый

слой. Затем находим вектор по формуле

с одной нулевой компонентой, соответствующей событию 6, которое образует второй слой. Аналогичными вычислениями, как видно из таблицы 3.2, находятся остальные слои и события, их составляющие.

50