
Учебное пособие 985
.pdf
Задачи и упражнения
1.5.Приведите пример сильно связного, односторонне связного, слабо связного, несвязного графов.
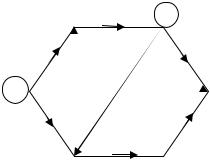
1.6.Среди графов, изображенных на рис. 1.10, указать сильно связный, односторонне связный, несвязный графы.
|
|
|
|
|
|
|
|
G1 |
G2 |
G3 |
G4 |
Рис. 1.10
1.3. Матричные представления графов
Понятия, которые вводятся в этом разделе, полезны при алгебраическом исследовании графов, а также при компьютерной обработке в том случае, когда число вершин и ребер графа настолько велико, что геометрическое представление теряет свою наглядность.
Пусть G = ( X ,U ) произвольный простой граф, число вершин которо-
го равно n .
Определение 1.19. Матрицей смежности графа G = ( X ,U ) называ-
ется квадратная матрица |
A размерности n × n , элементы которой опреде- |
|
ляются следующим образом: |
|
|
1, |
если вершины xi и x j соединены ребром (дугой), |
|
aij = |
0, |
в противном случае. |
|
||
Замечание. 1) Матрица смежности неорграфа всегда симметрическая; 2) Количество дуг, выходящих из i -ой вершины, – это сумма элементов i -ой строки. Количество дуг, входящих в i -ую вершины, – это сумма элементов i -го столбца.
Пример 1.9. Для неорграфа, изображенного на рис. 1.8 а) и орграфа, изображенного на рис. 1.4, матрицы смежности соответственно равны:
|
|
0 |
1 |
1 |
0 |
1 |
|
|
|
|
|
1 |
1 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
1 |
0 |
1 |
0 |
0 |
|
|
|
|
|
|
0 |
0 |
|
|
|
A1 |
= |
1 |
1 |
0 |
1 |
1 |
|
, |
A2 |
= |
0 |
0 |
||||
|
|
|
|
|
. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
0 |
1 |
|
|
|
|
0 |
0 |
1 |
0 |
1 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
0 |
1 |
1 |
0 |
|
|
|
|
1 |
0 |
1 |
0 |
||
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||
11
Определение 1.20. Матрицей инцидентности графа G = ( X ,U ) с n
вершинами и m ребрами называется матрица B размерности n × m , элементы которой определяются следующим образом:
1, если вершина xi является началом дугиu j , |
|
|
|
bij = −1, если вершина xi является концом дугиu j , |
|
|
0, если вершина xi не инцидентна дугеu j |
|
|
Пример 1.10. Матрица инцидентности для неориентированного графа, изображенного на рис. 1.8 а):
|
|
u1 u2 u3 u4 u5 |
u6 |
u7 |
u8 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 1 0 0 0 1 0 |
0 |
1 |
||||||||
B = |
x2 |
|
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
|
x3 |
|
|
1 |
1 |
0 |
0 |
0 |
0 |
|
|
|
|
0 |
1 |
|||||||||
|
|
|
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
|
|
x4 |
|
|||||||||
|
|
|
|
0 |
0 |
1 |
1 |
1 |
0 |
|
|
|
x5 0 |
0 |
|||||||||
Матрица инцидентности для ориентированного графа, изображенного на рис. 1.8 б):
|
|
u1 |
u2 |
u3 |
u4 |
u5 |
u6 |
u7 |
|
|
|
|
|
|
|
|
|
− 1 0 |
|
|
|
|
x1 1 |
0 |
0 |
0 |
0 |
|||||
B = |
x2 |
|
− 1 1 |
0 |
0 |
0 |
− 1 1 |
|
||
x3 |
|
|
− 1 1 |
0 |
0 |
0 |
|
|
||
|
0 |
0 |
||||||||
|
x4 |
|
0 |
0 |
− 1 1 |
0 |
0 |
− 1 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
− 1 |
1 |
1 |
|
|
|
x5 0 |
0 |
||||||||
Задачи и упражнения
1.7. Для графа, приведенного на рисунке 1.11, найти: а) матрицу смежности; б) матрицу инцидентности.
x1
x2
x3
x6
x5 |
x4 |
Рис. 1.11
12
1.8. Построить граф по матрице смежности:
|
1 |
0 |
1 |
1 |
|
|
|
|
|
|
|
1 |
0 |
1 |
0 |
|
|
A = |
0 |
1 |
1 |
0 |
. |
|
|
||||
|
|
1 |
0 |
0 |
|
1 |
|
||||
1.4. Деревья
Понятие дерева как математического объекта было впервые предложено Киркгофом в связи с определением фундаментальных циклов, применяемых при анализе электрических цепей. Деревья занимают особое положение в теории графов из-за предельной простоты строения, и часто при решении какой-либо задачи на графах ее сначала исследуют на деревьях. Понятие дерева применяется при конструировании различных алгоритмов. Кратчайшее остовное дерево находит применение при решении задач, в которых необходимо связать n точек некоторой сетью так, чтобы общая длина «линий связи» была минимальна.
Определение 1.21. Деревом называется связный неорграф без цик- лов, имеющий не менее двух вершин.
Определение 1.22. Если G - граф с n вершинами, то остовным де- ревом (остовом) графа G называется всякий остовный подграф графа G ,
являющийся деревом.
Определение 1.23. Ориентированным деревом с корнем r X назы-
вается ориентированный граф G = ( X ,U ) без циклов, в котором полустепень захода каждой вершины, за исключением одной r , равна 1, а полустепень захода вершины r равна 0.
Примером ориентированного дерева может служить "генеалогическое" дерево, в котором вершины соответствуют лицам мужского пола, а дуги ориентированы от родителей к детям. Корень в этом дереве соответствует "основателю" рода.
Рассмотрим следующую практическую задачу. Пусть имеется ряд городов, которые предполагается соединить авиалиниями. Как выбрать маршруты, чтобы из любого города можно было попасть в любой другой (с пересадками) и общая длина маршрутов было наименьшей? Пусть вершинами графа служат города, а дугами – возможные маршруты самолетов, пусть длина дуги равна длине соответствующего маршрута. Таким образом, практической задаче сопоставляется математическая задача о кратчайшем остовном дереве.
Другим примером служит построение кратчайшей коммуникационной сети. Пусть на некоторой территории размещены пункты, которые надо связать коммуникационной сетью минимальной стоимости. Предположим, что в результате изысканий определены возможные трассы для про-
13
кладки коммуникаций и оценена стоимость создания каждой трассы. Сопоставим каждому пункту сети вершину графа, две вершины будут соединены дугой, если только соответствующие пункты соединены возможной трассой коммуникации. Каждой дуге сопоставим число, равное стоимости строительства соответствующей коммуникации, и назовем его длиной дуги. Оптимальной структуре коммуникационной сети будет соответствовать кратчайшее дерево.
|
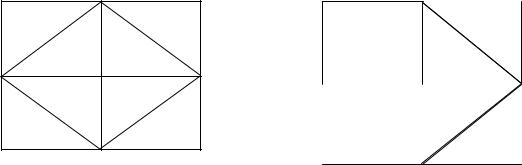
Пример 1.11. На рис. 1.12 а) – данный граф, б) – |
остов графа, в) – |
||||||||
другой остов графа. |
|
|
|
|
|
|
|
|
||
|
x 2 |
|
x 2 |
|
|
x 2 |
||||
|
|
x 3 |
|
|
|
|||||
|
|
|
x 3 |
|
|
|
|
|
x 3 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
x 1 |
x 4 |
|
x 1 |
x 4 |
|
x |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 5 |
|
x 5 |
x 1 |
|
|
|
|
x 5 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
x 6 |
|
|
|
|
|
|
|
x 6 |
|
|
x |
6 |
|
||||
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
x 7 |
|
x 7 |
|
|
x 7 |
||||
|
|
|
|
|
||||||
|
|
|
|
|
|
|
||||
|
а) |
|
б) |
|
|
|
|
в) |
||
|
|
|
|
Рис. 1.12 |
|
|
|
|
|
|
Рассмотрим некоторые свойства дерева. Хотя данное выше определение дерева просто для понимания, существует еще несколько других определений дерева, которые рассматриваются в следующей теореме.
Теорема 1.4. Пусть G - граф, у которого n вершин и m ребер ( n > 1). Тогда следующие свойства равносильны:
1)G связен и не содержит циклов, то есть G - дерево;
2)G связен и имеет (n − 1) ребро;
3)G не содержит циклов и имеет (n − 1) ребро;
4)всякая пара вершин соединена цепью и притом только одной;
5)G не содержит циклов, добавление ребра между любыми двумя несмежными вершинами приводит к появлению циклов.
Доказательство. Покажем, что из 1) 2) 3) 4) 5) 1), тогда все свойства равносильны. Воспользуемся индукцией по n .
При n = 2 утверждение тривиально. Пусть n > 2 .
Покажем, что из 1) 2). В дереве нет циклов, следовательно, согласно лемме 1.1, граф G − u имеет ровно две компоненты связности T1 и T2 , каждая из которых есть дерево. Пусть у графа Ti - ni вершин, mi ребер, i = 1,2 . По индуктивному предположению верны равенства
mi = ni − 1.
14
Далее имеем
m = m1 + m2 + 1 = n1 − 1 + n2 − 1 + 1 = (n1 + n2 ) − 1 = n − 1.
2) 3) Граф связен и m = n − 1. Требуется доказать, что в G нет циклов. Пусть, напротив, в графе G есть цикл и пусть u - ребро этого цикла. Тогда G − u связен (лемма 1.1) и имеет (n − 2) ребра, что противоречит теореме 1.3.
3) 4) Пусть k - число компонент связности G . Пусть, далее, компонента Ti граф, у которого ni - число вершин, mi - число ребер. Так как Ti - дерево, то mi = ni − 1. Теперь имеем
n −1 = m = m1 + m2 + ... + mk = (n1 −1) + (n2 −1) + ... + (nk −1) =
= (n1 + n2 + ... + nk ) − k = n − k n − 1 = n − k , k = 1.
Итак, G - связный граф и потому любые несовпадающие вершины xi и x j соединены в нем цепью. Предположим, что существует две несовпадающие цепи, соединяющие xi и x j , тогда согласно утверждению 1.1 их объединение содержит цикл, что противоречит нашему условию. Следовательно, каждые две вершины соединены единственной цепью.
4) 5) Предположим, что граф G содержит циклы. Пара несовпадающих вершин, принадлежащих одному циклу, соединена по меньшей мере двумя цепями, что противоречит условию. Следовательно, G ациклический. Пусть xi и x j - две его несмежные вершины. Присоединим к графу G ребро u = (xi , x j ) . В G есть цепь (xi , x j ) , которая в G + u дополняется до цикла. В силу утверждения 1.2 это цикл единственен.
5) 1) Требуется доказать, что граф G связен. Предположим противное, то есть, что вершины xi и x j принадлежат разным компонентам связности графа G . Тогда G + (xi , x j ) не имеет циклов, что противоречит 5). Следовательно, G связен и потому является деревом.
Далее, рассмотрим задачу о кратчайшем остовном дереве. Постановка задачи. Пусть дан связный неорграф G = ( X ,U ) , каж-
дому ребру u которого в соответствие поставлено число l(u) > 0 , называемое длиной этого ребра. Требуется найти остов графа G , общая длина ре-
бер которого минимальна.
Алгоритм Краскала построения кратчайшего остова взвешенного графа
Шаг 1. Начать с построения графа T , содержащего все n вершин исходного графа и не содержащего ни одного ребра.
Шаг 2. Составить список ребер графа G в порядке неубывания их весов.
Шаг 3. Начав с первого ребра в этом списке, добавлять по порядку ребра в графе T , соблюдая условие: такое добавление не должно приводить к появлению цикла в T , в противном случае это ребро пропускается.
15
Шаг 4. Повторять шаг 3 до тех пор, пока число ребер в T не станет |
|||||||||
равным n − 1. Получившееся дерево является кратчайшим остовом графа. |
|||||||||
Обоснование алгоритма Краскала весьма тривиально [2, гл. 7, § 3]. |
|||||||||
Пример 1.12. Найти кратчайший остов графа G , изображенного на |
|||||||||
рис. 1.13 а). Над ребрами графа указаны длина каждого ребра. |
|
|
|||||||
Шаг 1. Построим граф, содержащий все девять вершин графа, рис. |
|||||||||
1.13 б). |
|
|
|
|
|
|
|
|
|
Шаг 2. Расположим все ребра графа в порядке неубывания их длин: |
|||||||||
|
|
|
|
1 |
1 |
1 |
|
|
|
|
|
|
|
(x1 , x2 ) , (x1 , x4 ) , (x2 , x5 ) , |
|
|
|
||
|
|
|
|
2 |
2 |
2 |
|
|
|
|
|
|
|
(x2 , x4 ) , (x4 , x5 ) , (x6 , x8 ) , |
|
|
|
||
|
|
|
3 |
3 |
3 |
|
3 |
|
|
|
|
|
(x2 , x6 ) , (x5 , x6 ) , (x8 , x9 ) , (x7 , x8 ) , |
|
|
||||
|
|
|
|
4 |
4 |
|
|
|
|
|
|
|
|
(x3 , x6 ) , (x6 , x9 ) , |
|
|
|
||
|
|
|
5 |
5 |
6 |
|
7 |
|
|
|
|
|
(x2 , x3 ) , (x5 , x8 ) , (x4 , x7 ) , (x4 , x8 ) . |
|
|
||||
x 1 |
1 |
x 2 |
5 |
x 3 |
x 1 |
1 |
x 2 |
|
x 3 |
1 |
2 |
1 |
3 |
4 |
1 |
|
1 |
3 |
4 |
|
|
|
|
|
|
|
|
||
x 4 |
2 |
x 5 5 |
3 |
x 6 |
x 4 |
|
|
|
x 6 |
|
|
|
|
|
x 5 |
|
|||
6 |
|
2 |
4 |
|
|
|
|
||
7 |
|
|
|
|
2 |
|
|||
|
|
|
|
|
|
|
|
|
|
x 7 |
3 |
x 8 |
3 |
x 9 |
x 7 |
3 |
x 8 |
3 |
x 9 |
|
|
|
|
|
|||||
|
|
а) |
|
|
|
|
б) |
|
|
|
|
|
|
Рис. 1.13 |
|
|
|
|
|
Всего девять вершин, поэтому алгоритм закончится, когда будет |
|||||||||
внесено восемь ребер в граф. На рис. 1.13 б) представлено кратчайший ос- |
|||||||||
тов графа, его длина равна восемнадцати. |
|
|
|
|
|||||
Отметим, что полученное дерево не единственно, но его длина оди- |
|||||||||
накова для всех кратчайших остовных деревьев. |
|
|
|
|
|||||
Задачи и упражнения
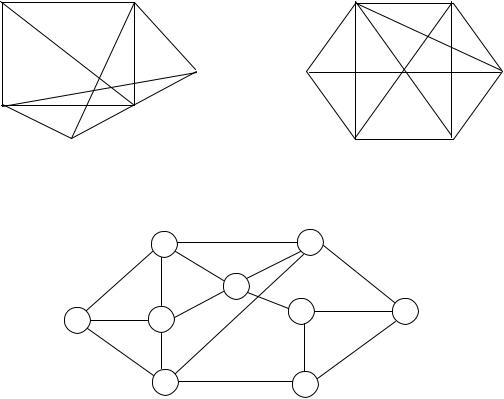
1.9.С помощью алгоритма Краскала найти кратчайший остов графов, изображенных на рис. 1.14.
1.10.Все площадки для отдыха, расположенные в горной лесопарковой зоне, необходимо соединить телефонной сетью, причем телефонные линии должны проходить вдоль троп лесопарковой зоны (рис. 1.15). Тре-
16
буется, спроектировать телефонную сеть с минимальной суммарной длиной линий.
4 |
|
|
5 |
|
|
|
5 |
18 |
|
12 |
11 |
10 |
6 |
|
|||
9 |
17 |
|
|
||
5 |
|
|
|
15 |
|
|
|
|
|
|
|
11 |
6 |
|
|
9 |
|
8 |
13 |
14 |
10 |
||
|
|
|
|
||
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
3 |
|
|
|
G1 |
|
G2 |
|
|
Рис. 1.14
|
|
p2 |
7 |
p6 |
|
|
|
|
|
|
|
||
|
1 |
6 |
|
5 |
|
2 |
|
4 |
|
|
|
||
|
p5 |
|
|
|
||
|
|
4 |
|
|
||
|
|
3 |
|
|
||
|
|
|
|
|
||
p1 |
1 |
p3 |
1 |
p8 |
9 |
p9 |
|
|
|
||||
|
|
|
|
|
|
|
|
1 |
5 |
|
4 |
|
6 |
|
|
7 |
|
|
||
|
|
|
|
|
||
|
|
p4 |
p7 |
|
|
|
|
|
|
|
|
Рис. 1.15
1.5. Эйлеровы и гамильтоновы графы
Как уже было отмечено, одна из самых первых задач теории графов – это задача о кенигсбергских мостах. Можно ли, начав с некоторой точки совершить прогулку и вернуться в исходную точку, пройдя по каждому мосту ровно один раз. Многие были убеждены, что у этой задачи нет решения. Однако лишь в 1736 году швейцарский математик Л. Эйлер доказал возможность решения задачи и дал отрицательный ответ на поставленный вопрос, так как соответствующий граф не содержал эйлерова цикла. С эйлеровыми графами также связана задача китайского почтальона: ребрам графа приписаны положительные веса, требуется найти цикл, проходящий через каждое ребро, по крайней мере, один раз и такой, что его суммарный вес минимален. Очевидно, что если такой граф содержит эйлеров цикл, то он и будет оптимальным. Эта задача имеет много потенциальных приложений, связанных с проблемой инспектирования распределенных систем, когда требуется проверить все «компоненты». Например, проверка электрических, телефонных или железнодорожных линий. Другие приложения могут быть связаны с отысканием наилучшего метода работы автоматических вентиляционных устройств, составлением оптимального маршрута при уборке помещений и коридоров в больших учреждениях.
17
В 1859 году другой известный математик Гамильтон придумал игру, где использовался додекаэдр, всем вершинам которого были даны названия известных городов. Задача играющего состояла в том, чтобы определить замкнутый путь через все города, посетив каждый из них только один раз. Так возникло понятие гамильтонова пути во взвешенном графе. Практические приложения этой задачи весьма разнообразны. Так в ряде отраслей промышленности, особенно химической и фармацевтической возникает следующая основная задача планирования. Нужно произвести n продуктов, используя единственный тип аппаратуры. Аппарат должен или не должен быть перенастроен после того, как произведен продукт pi в зави-
симости от комбинации ( pi , p j ) . Стоимость перенастройки аппаратуры постоянна и не зависит от продукта, который только что произведен, или от продукта, следующего за ним, при этом не требуется никаких затрат, если перенастройка аппаратуры не нужна. Предположим, что продукты производятся в непрерывном цикле, так что после производства последнего из n продуктов снова возобновляется в том же фиксированном цикле производство первого продукта. Возникает вопрос, может ли быть найдена циклическая последовательность производства продуктов, не требующая перенастройки аппаратуры. Пусть G - ориентированный граф, вершины которого представляют продукты, а существование дуги ( pi , p j ) означает, что продукт p j может следовать за продуктом pi без перенастройки аппаратуры. Ответ на поставленный вопрос зависит от того, имеет ли данный граф гамильтонов контур или нет. Если нет, то какова должна быть последовательность производства с наименьшими затратами на перенастройку.
Другой задачей, связанной с понятием гамильтонова пути, является задача коммивояжера: коммивояжер должен посетить каждый из задан-
ных n городов, выехав из некоторого города и вернувшись в него же. Требуется найти кратчайший маршрут, зная расстояние между каждой парой городов. С точки зрения теории графов, задача коммивояжера сводится к поиску гамильтонова цикла минимального веса в полном взвешенном графе, если под весом цикла понимается сумма весов составляющих его ребер. Задача коммивояжера и ее варианты имеют большое число практических приложений в различных областях человеческой деятельности. Например, ее приложениями являются задачи сбора почтовых отправлений из почтовых ящиков, составления расписания выполнения операций на машинах, проектирования электрических сетей, управления автоматическими линиями и т.д.
Таким образом, эйлеровы и гамильтоновы графы часто встречаются в практических задачах и поэтому представляют особый интерес. Рассмотрим более подробно эти понятия.
Определение 1.24. Цикл (цепь), который(-ая) проходит ровно один раз по каждому ребру неориенированного графа G , называется эйлеровым циклом (эйлеровой цепью). Граф, в котором существует эйлеров цикл, на-
зывается эйлеровым графом.
18
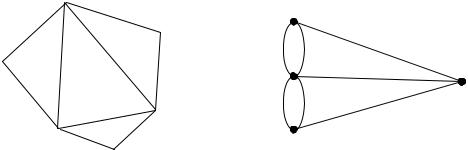
Пример 1.13. На рис. 1.16 а) изображен эйлеров граф, поскольку он содержит эйлеров цикл (1, 2, 3, 4, 5, 6, 4, 2, 6, 1). На рис. 1.16 б) изображен
неэйлеров граф.
2
|
C |
|
|
3 |
|
1 |
A |
|
|
D |
|
|
|
|
|
4 |
|
6 |
B |
|
|
|
|
а) |
5 |
б) |
|
||
|
Рис. 1.16 |
|
Очевидно, что не все графы имеют эйлеров цикл. Более того, справедливо следующее утверждение: почти нет эйлеровых графов (Р.Рейд,
1962 г.).
Теорема 1.5. (Л.Эйлер, 1736 г.) [3, гл.7, § 43] Связный неорграф является эйлеровым тогда и только тогда, когда степени всех его вершин четны.
Понятие эйлеровости можно распространить и на орграфы. Имеет место следующая
Теорема 1.6. Связный орграф G = ( X ,U ) содержит эйлеров контур
(эйлеров путь) тогда и только тогда, когда полустепени захода d + (xi ) и
полустепени исхода d − (xi ) всех вершин удовлетворяют условиям:
для случая контура d + (xi ) = d − (xi ) для всех xi X ; |
|
|
|
для случая |
пути d + (xi ) = d − (xi ) для всех |
xi |
¹ p или q , |
d + ( p) = d − ( p) − 1, |
d − (q) = d + (q) + 1, где p -начальная, а |
q - |
конечная |
вершина эйлерова пути.
Естественно возникает вопрос: как найти хотя бы один эйлеров цикл в эйлеровом графе? Для определения эйлерова цикла в неорграфе используется метод Флери, идея которого заключается в следующем: начав с некоторой вершины, каждый раз вычеркивать пройденное ребро; не проходить по ребру, если удаление этого ребра приводит к разбиению графа на две связные компоненты (не считая изолированных вершин).
Определение 1.25. Путь, проходящий через все вершины графа в точности по одному разу через каждую, называется гамильтоновым пу-
тем. Если начальная и конечная вершина этого пути совпадают, то такой путь называется гамильтоновым контуром. Граф, в котором существует гамильтонов контур, называется гамильтоновым графом.
В неорграфе рассматривают гамильтоновы циклы и цепи.
Пример 1.14. Граф, представленный на рис. 1.17 а), является гамильтоновым, так как последовательность его ребер u1 , u2 , u3 , u4 , u5 , u6 , образу-
19
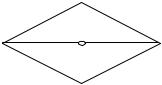
ет гамильтонов цикл. Граф на рис. 1.17 б) имеет гамильтонов путь, состоящий из ребер u1 , u2 , u2 , u2 , но не имеет гамильтонова цикла.
|
u6 |
u5 |
|
u4 |
u5 |
|
|
|
|
|
|
||
|
|
|
|
|
u6 |
u1 |
u1 |
u7 |
|
|
u4 |
u2 |
|
|
|
|
|
|
u3 |
|
|
|
|
|
|
|
|
|
u2 |
u3 |
|
|
|
|
|
|
а) |
|
|
|
б) |
|
|
|
|
Рис. 1.17 |
|
|
Несмотря на внешнее сходство постановок, задачи распознавания эйлеровости и гамильтоновости графа принципиально различны. Пока неизвестно никакого простого критерия или алгебраического метода, позволяющего ответить на вопрос, существует или нет в произвольном графе гамильтонов цикл или контур. Интуитивно ясно, что если граф содержит много ребер и эти ребра к тому же достаточно равномерно распределены, то граф «предрасположен» быть гамильтоновым. В приводимых ниже тео-
ремах можно усмотреть подтверждение этому. |
|
|||
|
Теорема 1.7. Если G - сильно связный граф на n вершинах без пе- |
|||
тель, |
для |
любой вершины x |
которого справедливо |
неравенство |
d + (x) + d − (x) ³ n , то G имеет гамильтонов контур. |
|
|||
|
Теорема 1.8. Простой орграф G , имеющий последовательность сте- |
|||
пеней |
d1 £ d 2 £ ... £ d n является |
гамильтоновым, если из |
того, что |
|
d k £ k £ n / 2 |
следует d n−k ³ n - k , где n - количество вершин графа. |
|||
Отметим, что указанные критерии представляют теоретический интерес, но являются слишком общими и не пригодны для произвольных графов, встречающихся на практике. С другой стороны, существующие алгебраические методы определения гамильтоновых циклов не могут быть применены к задачам с более чем несколькими десятками вершин, так как требуют слишком большого времени работы и большой памяти компьютера. Более приемлемыми являются методы перебора, например, метод Робертса и Флореса [2] и мультицепной метод, которые не предъявляют чрезмерных требований к памяти компьютера.
Рассмотрим алгоритм алгебраического метода определения гамильтоновых путей и контуров. Сначала введем ряд определений.
Внутреннее произведение вершин пути [x1 ,..., xk ] определяется как
выражение вида x2 × x3 ... × xk −1 , не содержащее концевые вершины x1 и xk .
Модифицированная матрица смежности B - это матрица размерно-
сти n × n , элементы которой определяются следующим образом:
20
