
Учебное пособие 790
.pdf
Рассмотрим решение линейного однородного уравнения. Для этого разделим переменные
dyy = −P (x)dx; ln y = −∫P (x)dx +ln C ,
откуда y = Ce−∫P(x)dx , где С — постоянная интегрирования.
Варьируя постоянную интегрирования, т. е. считая С(х) - некоторой дифференцируемой функцией от х, подлежащей определению, имеем
y = C (x)e−∫P(x)dx .
Подставляя y в неоднородное уравнение (1), получим
C′(x)e−∫P(x)dx = Q (x), откуда C (x)= ∫Q (x)e∫P(x)dx dx +C .
Таким образом, искомое общее решение неоднородного линейного уравнения примет вид
y = e−∫P(x)dx |
∫Q (x)e∫P(x)dx dx +C |
, |
(5) |
|
|
|
|
где С - постоянная интегрирования.
Метод Лагранжа (или вариации произвольной постоянной) может быть применен и к уравнению Бернулли (4).
4°. В ряде случаев уравнения приводятся к линейным или уравнению Бернулли, если принять у за независимую
переменную, а x |
- за функцию. |
|
|
|
|
|||||||||
|
3.1. Решить |
уравнения: |
|
а) y′− yctgx = sin x ; |
|
|
||||||||
|
( |
2 |
|
) |
′ |
|
|
|
|
|
|
|
|
|
б) x |
|
+1 y |
|
+4xy = 3, |
найти |
решение, |
|
удовлетворяющее |
||||||
начальному условию y(1) = 0. |
|
′ |
′ |
′ |
|
|||||||||
|
Решение. а) Производя замену у=uv; y |
получим |
||||||||||||
|
|
= u v +uv |
|
|||||||||||
′ |
|
|
′ |
−uvctgx = sin x , |
или |
|
|
|
|
|
|
|||
u v +uv |
−vctgx)= sin x |
|
|
|
||||||||||
|
|
|
|
|
|
|
′ |
′ |
. |
|
(6) |
|||
|
|
|
|
|
|
|
u v +u (v |
|
||||||
10

Выберем v так, чтобы dvdx −vctgx = 0 . Разделяя переменные,
находим |
dv |
= ctgx dx , откуда v = sin x . Подставляя в уравнение |
||||||||||||||||||||||||||||||||||||||||
|
v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(6) значение v, получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
sin x du |
= sin x или du = dx; |
u = x +C . |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Общее решение будет y = (x +C )sin x . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
б) Приведем |
|
|
уравнение |
|
|
|
к |
виду |
|
|
y′+ |
4x |
y = |
|
3 |
и |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
x2 +1 |
x2 +1 |
||||||||||||||||||||||||||||||||||
сделаем замену y = uv, тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
′ |
′ |
|
|
4x |
|
|
|
|
|
3 |
|
|
|
|
|
|
′ |
|
|
|
|
|
′ |
|
|
4xv |
|
|
|
3 |
|
|
|
|||||||||
u v +v u + |
|
|
|
|
|
|
|
uv = |
|
|
|
|
|
; |
|
|
u v +u v |
+ |
|
|
|
|
|
|
= |
|
|
|
|
|
. |
(7) |
||||||||||
|
x |
2 |
+1 |
x |
2 |
+1 |
|
|
x |
2 |
|
|
|
x |
2 |
+1 |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+1 |
|
|
|
|
|
|||||||||||||||
Приравниваем выражение в скобках нулю |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
dv |
+ |
|
4x |
|
v = |
|
dv |
= − |
|
4xdx |
|
|
|
|
v |
|
= −2ln (x |
2 |
+1); |
|
||||||||||||||||||||||
dx |
|
0; |
v |
|
; |
|
ln |
|
|
|
||||||||||||||||||||||||||||||||
x2 +1 |
x2 +1 |
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v = |
|
|
|
1 |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 +1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Подставляя частное решение v |
в выражение (7), получим |
|||||||||||||||||||||||||||||||||||||||||
|
du |
|
= 3(x2 |
+1); u = 3∫(x2 +1)dx = x3 +3x +C . |
|
|
||||||||||||||||||||||||||||||||||||
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Общее решение примет вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
y = |
x3 |
|
+3x +C |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
x2 + |
) |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Для нахождения постоянной интегрирования воспользуемся начальным условием y=0 при х=1, тогда С=- 4. Окончательно будем иметь
y = x3 +3x −24 .
(x2 +1)
3.2. Найти общий интеграл уравнения:
11
а) (y2 −6x)y′+2 y = 0 ; б) xy′+3y = x2 .
Решение. а) Уравнение сводится к линейному, если считать у за независимую переменную, а х - за функцию. Запишем исходное уравнение в виде
|
|
|
dx |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
y |
|
|
|
||||||
|
2 y dy = −y |
|
|
+6x или x′− |
|
x = − |
|
. |
|
|
|
||||||||||||||||||||
|
|
|
y |
2 |
|
|
|
||||||||||||||||||||||||
Используя замену |
х = uv; |
|
x |
′ |
′ |
|
|
|
′ |
|
|
, получим |
|
||||||||||||||||||
|
|
|
= u v +v u |
|
|||||||||||||||||||||||||||
′ |
′ |
|
3 |
uv |
|
|
|
|
y |
|
|
|
|
|
|
′ |
|
|
′ |
|
|
3v |
|
y |
|
|
|||||
|
|
|
= − |
|
; |
|
|
|
|
|
|
|
− |
|
|
= − |
|
; |
(8) |
||||||||||||
u v +v u − |
|
|
y |
2 |
|
|
u v +u v |
y |
|
2 |
|||||||||||||||||||||
|
|
|
|
|
3v |
|
|
dv |
|
|
|
dy |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
v′ = |
|
|
|
|
|
|
|
|
v = y |
3 |
|
|
|
|
|
|
|||||||||||
|
|
|
|
y ; |
|
v |
|
= 3 y |
; |
|
|
. |
|
|
|
|
|
||||||||||||||
Подставляя |
частное решение v |
в выражение (8), будем |
|||||||||||||||||||||||||||||
иметь |
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
1 dy |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
′ |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
u y |
|
|
= − |
|
, du = − |
2 y2 |
, |
u = |
|
+C. |
|
|
|
|||||||||||||||||
|
|
|
2 |
2 y |
|
|
|
||||||||||||||||||||||||
Таким образом, окончательно получим |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
x = |
|
|
|
|
|
|
+C y |
. |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
б) Воспользуемся методом Лагранжа. Найдем сначала решение однородного уравнения ху'+Зу = 0. Разделим переменные
|
|
|
|
|
dy |
= −3dx |
, |
ln |
|
y |
|
= −3ln |
|
x |
|
+ln |
|
C |
|
, |
y = |
|
C |
. |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
y |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x3 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Пусть постоянная интегрирования зависит от |
х, т. е. |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
y = |
|
C (x) |
, |
|
|
|
|
|
(9) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
1 |
|
dC −3Cx−4 . |
|
|
x3 |
|
|
|
|
|
|
||||||||||||
тогда |
y = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
x3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Подставим у' и у в исходное уравнение |
|
|
|
|
|
|
||||||||||||||||||||||
x |
1 dC |
−3Cx−4 |
|
+ 3C |
|
= x2 , dC = x4 , C (x) |
= |
x5 |
+C . |
|||||||||||||||||||
|
|
3 |
|
|
|
|
|
|
||||||||||||||||||||
|
|
dx |
|
x |
3 |
|
|
dx |
|
5 |
1 |
|||||||||||||||||
|
x |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
12
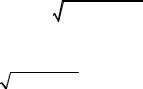
Таким образом, из выражения (9) имеем
|
|
|
|
|
|
|
|
|
|
|
|
|
x5 |
|
+C |
|
|
|
|
x |
2 |
|
|
|
|
|
C1 |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
y = |
|
|
|
|
|
|
|
1 |
|
= |
|
|
|
|
+ |
|
|
. |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
x3 |
|
|
|
|
|
||||||||||||||||||
3.3. Найти решение уравнений: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
а) y |
′ |
− yctgx |
= |
|
y3 |
|
; б) x |
2 |
y |
2 |
y |
′ |
+ xy |
3 |
=1; |
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
sin x |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
Решение. а) Данное уравнение есть уравнение Бернулли. |
||||||||||||||||||||||||||||||||||||||||||||||||
Для его решения используем подстановку у = uv, тогда |
||||||||||||||||||||||||||||||||||||||||||||||||
′ |
|
′ |
|
|
|
|
(uv)3 |
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
′ |
−vctgx)= |
(uv)3 |
(10) |
|||||||||||||||||||||
u v +v u −uvctgx = sin x , u v +u (v |
|
|
sin x , |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
dv = cos xdx , |
ln |
|
v |
|
= ln |
|
sin x |
|
; v = sin x . |
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
v |
|
|
sin x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Подставляя частное решение в уравнение (10), получим |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
′ |
sin x |
= u |
3 |
sin |
2 |
|
|
x, |
|
du |
= sin xdx, |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
u3 |
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
u |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
= cos x +C |
|
, |
|
u = |
|
|
|
|
1 |
|
|
|
|
. |
|
|||||||||||||||||||||||||
|
|
|
|
|
2u2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 cos x +2C |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
Таким образом, полагая 2C1 = C , имеем |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
y = |
|
|
|
|
|
|
|
|
sin x |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 cos x +C |
|
|
|
|
|
|||||||||||||||||||||||||
б) Разделим на x2 y2 |
правую и левую часть уравнения |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
y′+ x y |
|
= |
|
. |
|
|
|
|
|
|
|
(11) |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 y2 |
|
|
|
|
||||||||||||||||||||||||||||||
Теперь видно, что это уравнение Бернулли. Для его |
||||||||||||||||||||||||||||||||||||||||||||||||
решения воспользуемся методом Лагранжа. |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
Найдем сначала решение однородного уравнения |
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
y′+ |
y |
|
|
|
dy |
|
|
|
dx |
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
C |
|
, y = |
C |
|||||||||
|
|
= |
0, |
|
y |
= − |
x |
|
, ln |
= −ln |
+ln |
|
x . |
|||||||||||||||||||||||||||||||||||
|
x |
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Считаем, что C (х) - зависит от х, т. е.
13
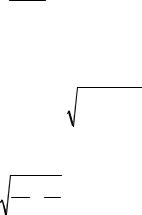
y = C (xx).
Подставим у и у' в исходное уравнение (11)
1 |
|
|
C |
|
|
C |
|
x2 |
2 |
|
|
|
x C′− |
|
|
|
+ |
|
= |
|
, C |
dC = xdx, |
|||
x2 |
|
x2 |
x2C2 |
|||||||||
C3 |
= |
x2 |
|
+C1 , C (x) |
= 3 3 x2 |
+3C1 . |
||||||
3 |
|
|||||||||||
2 |
|
|
|
|
|
|
2 |
|
|
|||
Таким образом, из выражения (12), полагая получим
y = 3 23x + xC3 .
(12)
3C1 = C ,
4. Уравнения в полных дифференциалах. Интегрирующий множитель
1°. Если для дифференциального уравнения
P (x, y)dx +Q (x, y)dy = 0 |
(1) |
||||
справедливо равенство |
|
|
|
|
|
∂P |
= |
∂Q |
, |
(2) |
|
∂y |
∂x |
||||
|
|
|
|||
то уравнение называется уравнением в полных дифференциалах
и может быть записано в виде du (х, y) = 0.
а) Общий интеграл находится по одной из формул
u (x, y)= ∫xx P (x, y)dx + ∫yy Q (x0 , y)dy = C, |
|
0 |
0 |
или |
(3) |
u (x, y)= ∫xx P (x, y0 )dx + ∫yy Q (x, y)dy = C, |
|
0 |
0 |
где x0 , y0 - координаты некоторой фиксированной точки,
причем
P2 (x0 , y0 )+Q2 (x0 , y0 )≠ 0 .
14
б) Поскольку полный дифференциал функции и равен сумме частных дифференциалов ∂∂ux dx = Pdx, ∂∂uy dy = Qdy , то
интегрируя их по отдельности, считая в первом случае у постоянной, а во втором х, найдем два выражения для функции
u = ∫Pdx +ϕ(y); u = ∫Qdy +ψ (x), |
(4) |
здесь ϕ(y) и ψ (x)- некоторые функции.
Общее решение находится подстановкой в первое выражение вместо ϕ(y) всех членов из второго выражения,
зависящих только от у, или наоборот.
2°. Пусть левая часть уравнения (1) не является полным
дифференциалом, |
однако можно найти такую функцию |
|||||
μ = μ(x, y), что |
умножая уравнение на нее, произведение |
|||||
μ = μ(Pdx +Qdy) |
будет полным дифференциалом |
|
||||
|
|
∂(μP) |
= |
∂(μQ) |
. |
(5) |
|
|
∂y |
|
|||
|
|
|
∂x |
|
||
Функция μ называется интегрирующим множителем и
легко находится в двух случаях:
а) если μ = μ(x), то из выражения (5) следует
|
∂P |
|
∂μ |
|
∂Q |
|
∂μ |
|
1 |
|
|
∂P − |
∂Q |
|
|
||
μ |
= Q |
+ μ |
или |
= |
|
|
dx. |
(6) |
|||||||||
∂y |
∂x |
∂x |
μ |
Q |
∂x |
||||||||||||
|
|
|
|
|
|
∂y |
|
|
|||||||||
б) если |
μ = μ(y), то из выражения (5) следует |
|
|||||||||||||||
|
∂μ |
|
∂P |
|
∂Q |
|
∂μ |
|
1 |
|
∂Q − ∂P |
|
|
||||
P |
+ μ |
= μ |
или |
= |
|
dy. |
(7) |
||||||||||
∂y |
∂y |
∂x |
|
|
|
|
|||||||||||
|
|
|
|
μ |
|
|
P |
∂x |
∂y |
|
|
||||||
Признаком существования интегрирующего множителя является отсутствие в выражении (6) переменной y, а в выражении (7) переменной х.
4.1. Решить уравнения: а) (x + y)dx +(x −2 y)dy = 0 ;
15
|
x |
|
x |
x |
|
|
|
|
y |
y |
|
|
|||||
б) x −e |
|
dx +e |
|
|
|
−1 |
|
dy = 0 . |
|
|
|
||||||
|
|
|
|
y |
|
|
||
|
|
|
|
|
|
|
|
|
Решение. а) Вначале надо убедиться, что данное уравнение в полных дифференциалах. Полагая P = x + y; Q = x - 2у, подставляем их значения в выражение (2)
|
|
∂(x + y) |
= |
∂(x −2 y) |
=1 . |
||||||||||||
|
|
∂y |
|
|
|
|
∂x |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Так как равенство справедливо, то общий интеграл |
|||||||||||||||||
находим по формуле (3), считая, что x0 |
= 0, y0 = 0 |
||||||||||||||||
u = ∫0x (x + y)dx −∫0y 2 ydy = |
x2 |
+ xy − y2 . |
|||||||||||||||
2 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
x2 |
|
|
|
|
|
2 |
|
|
|||
Отсюда общее решение |
|
|
|
+ xy − y |
|
= C . |
|||||||||||
2 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
x |
|
|
|
|
|
x |
|
x |
|
|
|
|||
|
P = x −e |
y |
|
Q = e |
y |
|
|
||||||||||
б) Полагая |
|
, |
|
|
|
|
−1 , подставляем их в |
||||||||||
|
|
|
y |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
выражение (2) и убеждаемся, что это уравнение в полных дифференциалах.
|
x |
|
|
|
x |
x |
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|||||||
|
|
y |
|
|
|
|
|
||||||
∂ x −e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂e |
−1 |
|
|
|
x |
|
|||
|
|
|
|
|
|
y |
|
|
x |
|
|
|
|
|
= |
|
|
= |
e |
y |
. |
||||||
∂y |
|
|
|
|
∂x |
|
y2 |
|
|||||
|
|
|
|
|
|
|
|
|
|
||||
Для нахождения функции и интегрируем ее частные дифференциалы по формулам (4), считая в первом случае у постоянной величиной, а во втором – х
|
|
|
|
|
|
|
|
x |
|
x |
2 |
|
|
|
x |
|
∫ |
|
∫ |
|
|
|
|
|
− ye y +ϕ(y), |
||||||||
Pdx = |
x −e y dx = |
|
||||||||||||||
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
|
∫ |
|
x |
x |
|
|
|
|
|
|
x |
+ψ (x). |
|||
Qdy = |
e |
y |
|
|
= −ye |
y |
|
|||||||||
|
|
y |
|
|
|
|
|
|||||||||
|
|
|
|
|
−1 dy |
|
|
|||||||||
16

Подставляя из первого выражения все члены, зависящие от x, во второе и приравнивая постоянной интегрирования,
|
x2 |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
получим |
− ye |
y |
= C . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x2 + y)dx − xdy = 0; |
||||||||||||||
4.2. Решить |
уравнения: |
|
|
а) |
|||||||||||||||||||||||||||||||||||
б) (xy2 + y)dx − xdy = 0 |
|
|
при условии |
y(1) =1. |
|||||||||||||||||||||||||||||||||||
Решение. а) Здесь P = x2 + y ; |
Q = - x. Подставляя Р и Q в |
||||||||||||||||||||||||||||||||||||||
выражение (6), |
получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
d μ |
|
= − 2dx ; ln |
|
μ |
|
= −2 ln |
|
x |
|
; μ = |
1 |
. |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
μ |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Умножим |
|
на |
интегрирующий |
|
множитель левую часть |
||||||||||||||||||||||||||||||||||
|
|
|
y |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
уравнения 1 |
+ |
|
|
|
dx − |
|
|
|
dy |
= 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
x |
2 |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Проверим по условию (5) - является ли это уравнение в |
|||||||||||||||||||||||||||||||||||||||
полных дифференциалах |
y |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
∂ 1 |
+ |
|
|
|
|
|
|
|
|
|
|
|
∂ |
− |
|
|
|
|
|
|
|
|
1 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
x |
2 |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
= |
|
|
|
. |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
∂y |
|
|
|
|
|
|
|
|
∂x |
|
|
|
|
x2 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Находим неопределенные интегралы |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
y |
+ϕ(y); |
||||||||||||
|
|
|
∫ |
μPdx = |
∫ |
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
x |
2 |
|
|
|
|
|
|
|
x |
|||||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
dx = x − |
|
|
|
||||||||||||||||||||||||
∫μQdy = −∫1x dy = − xy +ψ (x).
Так как во втором выражении нет членов, зависящих только от у, то есть ϕ(y)= 0 , то общее решение получается
из первого результата |
x − |
y |
= C . |
|
x |
||||
|
|
|
||
б) Здесь P = xy |
2 + y, |
Q = −x . Подставляя Р и Q в |
||
выражение (7), получим
17
|
d μ = |
|
1 |
|
|
|
|
|
|
|
(−1−2xy −1)dy |
= − |
2dy |
, |
|||||||||||||||||||
|
xy2 + y |
y |
|||||||||||||||||||||||||||||||
|
μ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
ln |
|
μ |
|
|
|
= −2 ln |
|
y |
|
, |
μ = |
|
1 |
. |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y2 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Умножим |
на |
|
|
интегрирующий |
множитель |
левую часть |
|||||||||||||||||||||||||||
|
|
1 |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
уравнения x + |
|
dx − |
|
|
dy = 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
y |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Проверим, является ли это уравнение в полных |
|||||||||||||||||||||||||||||||||
дифференциалах по условию (5) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
∂ x + |
|
|
|
∂ |
− |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
y |
|
|
2 |
|
|
|
1 |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
y |
|
= − |
|
. |
|
|||||||||||
|
|
|
|
|
|
|
∂y |
|
|
∂x |
|
|
y2 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Поскольку равенство выполнено, то частный интеграл находим по формуле (3), считая, что x0 =1, y0 =1, C = 0 .
x |
1 |
|
y |
1 |
|
x |
2 |
|
x |
|
|
x |
|
1 |
|
|
y |
|
x |
2 |
|
x |
− 3 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
∫1 |
x + |
dx −∫1 |
dy = |
|
+ |
|
|
|
+ |
|
|
|
= |
|
+ |
= 0, |
|||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
y |
||||||||||||
|
|
y |
|
y |
|
2 y |
|
1 |
|
y |
|
1 |
2 |
|
2 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
x2 y +2x = 3y.
5. Уравнения 1-го порядка, не разрешенные относительно производной
1 . Если дифференциальное уравнение является уравнением высшей степени относительно производной
. Если дифференциальное уравнение является уравнением высшей степени относительно производной
f (x, y, y′)= 0 , |
(1) |
то, разрешая его относительно y′, например, для случая второй степени, получим два уравнения
y′ = f1 (x, y) и y′ = f2 (x, y). |
(2) |
Геометрически это означает, что через каждую точку М некоторой плоской области проходят две интегральные кривые. Общее решение уравнения (1) в этом случае примет вид
18
F1 (x, y,C )= 0; F2 (x, y,C )= 0 . |
(3) |
Кроме того, уравнение (1) может иметь особое решение, которое может быть получено в результате исключения у' = р из системы уравнений
f (x, y, p)= 0; f p′ = (x, y, p)= 0 . |
(4) |
Геометрически особый интеграл представляет огибающую |
|
семейства кривых (3) |
|
F (x, y,C )≡ F1 (x, y,C ) F2 (x, y, C )= 0 |
(5) |
и может быть получен еще исключением С |
из системы |
уравнений |
|
F (x, y,C )= 0; FC′(x, y,C )= 0 . |
(6) |
Следует заметить, что кривые (4), (6), не всегда являются решениями уравнения (1) и в каждом конкретном случае
необходима проверка. |
|
|
|
|
|
|||
2°. Если уравнение имеет вид |
|
|
|
|||||
|
|
|
|
x =ϕ(y′), |
|
(7) |
|
|
то, полагая |
у' = р, получим x =ϕ(p). Дифференцируя по х, |
|||||||
считая |
р |
функцией |
х, |
получим |
dx =ϕ′(p)dp , |
так как |
||
′ |
|
|
|
′ |
(p)dp . |
|
|
|
dy = y dx = pdx , то |
dy = pϕ |
|
|
|
||||
Интегрируя последнее выражение, запишем решение |
||||||||
уравнения (7) в параметрическом виде |
|
|
|
|||||
|
|
x =ϕ(p); |
y = ∫pϕ′(p)dp +C . |
(8) |
||||
3°. Если уравнение имеет вид |
|
|
|
|||||
|
|
|
|
y =ϕ(y′), |
|
(9) |
||
то, полагая у' = р, |
получим x =ϕ(p). |
|
|
|
||||
Дифференцируя, будем иметь dy =ϕ′(p)dp . Учитывая, что |
||||||||
dy=pdx, |
получим |
pdx =ϕ′(p)dp , |
откуда dx = |
ϕ′(p)dp |
. |
|||
|
||||||||
|
|
|
|
|
|
|
p |
|
Интегрируя последнее выражение, общее решение примет вид
19
