
Учебное пособие 707
.pdf2°. Статические моменты тела относительно координатных плоскостей вычисляются по формулам
mxy |
= òòòd (x, y, z ) zdxdydz; |
|
||||||||||
|
|
|
V |
|
|
|
|
|
|
|
|
|
mxz |
= òòòd (x, y, z ) ydxdydz; |
(3) |
||||||||||
|
|
|
V |
|
|
|
|
|
|
|
|
|
myz |
= òòòd (x, y, z ) xdxdydz. |
|
||||||||||
|
|
|
V |
|
|
|
|
|
|
|
|
|
Координаты центра тяжести тела |
|
|
|
|
||||||||
x = |
myz |
; y |
c |
= |
m |
xz |
; |
z = |
mxy |
, |
(4) |
|
|
|
|
|
|
||||||||
c |
m |
|
|
m |
c |
m |
|
|
||||
|
|
|
|
|
|
|
|
|||||
где m - масса тела.
3°. Моменты инерции тела относительно координатных осей
Ix |
= òòòd (x, y, z )(y2 |
+ z 2 )dxdydz; |
|
|||||
|
|
|
V |
|
( |
|
|
|
I |
y |
= |
òòò |
d (x, y, z ) |
x2 |
+ z2 dxdydz; |
(5) |
|
|
|
|
|
) |
|
|||
|
|
|
V |
|
|
|
|
|
Iz |
= òòòd (x, y, z )(x2 + y2 )dxdydz. |
|
||||||
|
|
|
V |
|
|
|
|
|
4°. Моменты инерции относительно координатных плоскостей
Ixy = òd (x, y, z )z2dV ;
V
Ixz = òd (x, y, z ) y2dV ; |
(6) |
V
I yz = òd (x, y, z )x2dV ,
V
где dV= dxdydz.
Полярный момент инерции равен
41

I0 = Ixy + Ixz + I yz = òd (x, y, z )(x2 + y2 + z 2 )dV . |
(7) |
V |
|
5°. Если в теле объема V непрерывным образом распределены массы с заданной в каждой точкеМ (x,y,z) плотностью d (M ) = d (x, y, z ) , ТО проекции на оси координат полной силы
r
притяжения F на точку A(xc,yc,zc), в которой, мы считаем, сосредоточена единица массы, согласно закону притяжения Ньютона, определяются по формулам
Fx |
= ò |
x - x |
d dV ; Fy |
= ò |
y - y |
c |
|
d dV ; Fz = ò |
z - z |
c |
ddV , (8) |
||||||
|
|
c |
|
|
|
|
|
||||||||||
r |
3 |
|
r |
3 |
|
r |
3 |
|
|||||||||
|
V |
|
|
|
|
V |
|
|
|
|
V |
|
|
|
|||
где r = |
(x - x |
|
)2 |
+ (y - y |
c |
)2 + (z - z |
c |
)2 - расстояние МA. |
|||||||||
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
||||
6°. Ньютоновское поле потенциально. Выражение для потенциала поля тела объемаV с плотностью d на точку А имеет вид
W = ò |
d dV |
(9) |
|
r |
|||
V |
|
Если тело однородно, то в приведенных формулах следует положить d (x, y, z ) =1 .
7.1. Найти объем тела, ограниченного поверхностями:
а) z = x2 + y2 , z = x2 + 2 y, y = x, y = 2x, x =1;
б) x2 + y2 = z 2 , x2 + y2 + z2 = a2 , внутри конуса;
Решение. а) Объем тела в декартовой системе координат определяется по формуле
V = òòòdxdydz .
|
|
|
|
V |
|
|
|
Тело |
сверху |
и |
снизу |
ограничено |
параболлойдам |
||
z = x2 + 2 y2 и |
z = x2 + y2 . |
Проекция |
тела |
на плоскостьОху |
|||
показана |
на |
рис. 29. |
Расставляя |
пределы |
интегрирования, |
||
42

получим
1 |
2 x |
x2 +2 y2 |
1 |
2 x |
|
1 |
1 |
|
7 |
|
||
V = òdx ò dy ò dz = òdx ò |
y 2dy = |
ò7x3dx = |
|
. |
||||||||
|
12 |
|||||||||||
0 |
x |
2 |
+ y |
2 |
0 |
x |
3 |
0 |
|
|||
x |
|
|
|
|
|
|
||||||
Рис. 29
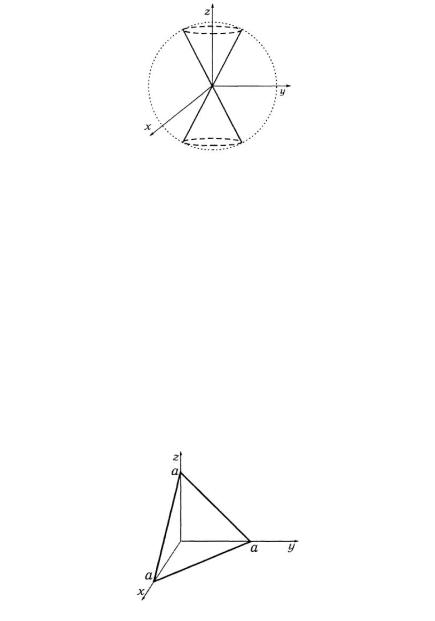
б) Представим искомый объем на рис. 30. Поскольку тело,
заключенное |
внутри |
конуса, симметрично |
относительно |
|||||||||||||||
начала |
|
координат, |
то |
его |
|
объем |
в сферической системе |
|||||||||||
координат равен |
|
|
|
|
|
|
p |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
2p |
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|||
V = 2òòòr2 sinqd rdqdj = 2 ò djòsinqdq òr2d r = |
||||||||||||||||||
|
|
G |
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
0 |
|
|
|
|
|
2p |
|
|
p |
|
4p a |
3 |
æ |
|
|
|
|
|
ö |
|
|
|
2 |
|
|
|
4 |
|
|
|
2 |
|
|
|||||||
= - |
a3 |
ò |
cosq |
|
|
|
dj = |
|
ç1 |
- |
|
÷. |
|
|||||
|
|
|
|
|
|
|
|
|||||||||||
|
3 |
|
|
|
|
|
|
3 |
|
ç |
|
2 |
|
|
÷ |
|
||
|
|
0 |
|
|
0 |
|
|
|
è |
|
|
|
ø |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
43
|
|
|
|
|
|
Рис. 30 |
|
|
|
|
|
|
|
|
|
|
|
|||||
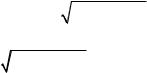
7.2. Определить массу: а) пирамиды, ограниченной плос- |
|
|||||||||||||||||||||
костями x + y + z = a, х = 0, y = 0, z = 0, если плотность в |
|
|||||||||||||||||||||
каждой ее точке равна аппликатеz этой точки; б) сферичес- |
|
|||||||||||||||||||||
кого слоя между поверхностями x2+y2+z2=R2 и х2 + у2 + z2 = |
|
|||||||||||||||||||||
4R2, |
если |
плотность |
|
в |
|
|
|
каждой |
его |
точке |
обра |
|||||||||||
пропорциональна расстоянию точки от начала координат. |
|
|||||||||||||||||||||
Решение, а) Пирамида показана на рис. 31. Поскольку по |
|
|||||||||||||||||||||
условию |
задачи плотность d (x, y, z ) = z , |
то, |
пользуясь |
|
фор- |
|
||||||||||||||||
мулой (2), будем иметь |
|
a-x- y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
a |
a-x |
|
|
|
|
|
1 |
a a-x |
|
|
|
|
|
|
||||
m = òòò zdxdydz = òdx ò dy |
ò zdz = |
òdx ò (a - x - y )2 dy = |
|
|||||||||||||||||||
2 |
|
|||||||||||||||||||||
|
|
V |
|
0 |
0 |
0 |
|
|
|
|
|
0 |
|
0 |
|
|
|
|
|
|
||
|
1 |
a æ |
|
|
|
|
y |
3 |
ö |
|
a-x |
|
|
|
1 |
a |
|
a |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
= |
ç |
(a - x)2 y - (a - y ) y 2 + |
|
÷ |
|
|
dx = |
(a - x )3 dx = |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||
2 |
ò0 è |
|
|
|
3 |
ø |
|
0 |
|
|
6 |
ò0 |
24. |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Рис. 31
44
|
б) Поскольку расстояние точки от начала координат |
||||||||||||||||||||||||||||||||||||
определяется |
|
выражением x2 + y2 + z2 |
то |
|
|
|
|
плотность |
будет |
||||||||||||||||||||||||||||
равна |
d (x, y, z ) = |
1 |
|
|
|
. |
Пользуясь |
|
|
|
формулой (2) в |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
x2 + y2 + z2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
сферической системе координат, получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
2p |
|
p |
|
|
|
|
|
|
|
|
2 R |
|
|
|
|
|
|||||
|
m = òòò |
r 2 sinqd rdq dj = ò djòsin qdq ò rd r = |
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
G |
r |
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
3 |
|
2p |
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
= - |
|
R2 ò cosq |
|
dj = 6p R2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
2 |
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
7.3. Найти координаты центра тяжести однородного тела, |
||||||||||||||||||||||||||||||||||||
ограниченного поверхностями: х + у + z=1, х = 0 у = 0, z = 0. |
|||||||||||||||||||||||||||||||||||||
|
Решение. Масса тела определяется по формуле (2) |
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
1 |
1-x |
1-x- y |
1 |
|
1-x |
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
1 |
|
|
|
|
|
|
|||||||||||
m = òdx ò dy ò dz = òdx ò (1- x - y )dy = |
|
ò |
(1- x )2 dx = |
. |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||
|
0 |
0 |
|
0 |
|
0 |
|
0 |
|
|
|
|
|
|
|
|
2 |
|
0 |
|
6 |
|
|
|
|
|
|
||||||||||
|
По формулам (3) находим статические моменты |
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
1 |
1-x |
1-x- y |
|
1 |
|
1 1-x |
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
1 |
|
|||||||||||||
mxy |
= òdx ò dy |
|
ò zdz = |
|
òdx ò (1- x - y )dy = |
ò(1- x )3 dx = |
|
; |
|||||||||||||||||||||||||||||
|
|
6 |
24 |
||||||||||||||||||||||||||||||||||
|
0 |
0 |
|
0 |
|
|
2 |
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|||||||||||
|
1 |
1-x |
|
1-x- y |
1 |
|
1-x |
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
1 |
|
|
|
||||||||||
mxz |
= òdx ò ydy |
ò |
|
dz = òdx ò y (1- x - y )dy = |
ò(1- x )3 dx = |
|
; |
||||||||||||||||||||||||||||||
|
6 |
24 |
|||||||||||||||||||||||||||||||||||
|
0 |
0 |
|
0 |
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
||||||||||||
|
1 |
1-x |
|
1-x- y |
1 |
|
1-x |
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
1 |
|
|
|
|||||||||||
myz |
= ò xdx ò dy |
ò |
|
dz = ò xdx ò (1- x - y )dy = |
ò(1- x )2 dx = |
|
. |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
0 |
0 |
|
0 |
|
0 |
|
0 |
|
|
|
|
|
|
|
2 |
|
0 |
24 |
|
|
|
|||||||||||||||
|
Таким образом, по формулам (4) |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
x |
= y |
|
= z |
c |
= |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
c |
|
c |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
7.4. |
Найти |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
координаты |
|
|
центра |
|
|
|
|
тяжести |
|
|
|
|
сферы |
|||||||||||||||||||||||
x2 + y2 + z2 = 2az , |
если |
плотность |
в |
точках сферы обратно |
|||||||||||||||||||||||||||||||||
пропорциональна расстоянию этих точек от начала координат.
45
Решение. Центр сферы сдвинут по осиOz на величину радиуса. По соображениям симметрии, очевидно, что хс и ус
равны 0.
По условию задачи плотность равнаd = |
1 |
, |
|
x2 + y2 + z2 |
|||
|
|
тогда
m = òòò |
|
dxdydz |
|
. |
|||
x |
2 |
+ y |
2 |
+ z |
2 |
||
V |
|
|
|
|
|||
Переходя к сферическим координатам и расставляя пределы интегрирования по V, будем иметь
|
p |
|
|
|
p |
|
|
|
||
2p |
2 |
|
2 acosq |
2p |
|
2 |
|
4p a |
2 |
|
m = ò dj òsinqdq |
ò |
rd r = 2a2 ò dj òsinq cos2 qdq = |
|
. |
||||||
3 |
|
|||||||||
0 |
0 |
|
0 |
0 |
0 |
|
|
|
||
Статический момент относительно плоскости Оху по формуле (3) равен
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
||
|
zdxdydz |
|
|
|
2p |
|
2 |
|
|
|
2 acosq |
2 |
|
||||||
mxy = òòò |
|
|
= |
ò djòsinq cosqdq ò r |
d r = |
||||||||||||||
x |
2 |
+ y |
2 |
+ z |
2 |
|
|
||||||||||||
V |
|
|
|
|
|
0 |
0 |
|
|
0 |
|
|
|||||||
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
16pa |
|
|
|
|||
= - |
16a p |
|
òcos4 q d cosq = |
|
. |
|
|
||||||||||||
|
|
|
|
|
|||||||||||||||
|
|
|
3 |
|
0 |
|
4 |
|
|
|
|
|
|
15 |
|
|
|
|
|
Таким образом, zc |
|
= |
a . |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
46
БИБЛИОГРАФИЧЕСКИЙ СПИСОК |
|
|
1. Андрианова Т.Н. Задачник практикум |
по |
высшей |
математике / Т.Н. Андрианова.– СПб.: Изд-во |
Сант-Петерб. |
|
ун-та, 1994. |
|
|
2. Марон И.А. Дифференциальное и |
интегральное |
|
исчисление в примерах и задачах/ И.А. Марон. |
– М.: |
|
Физматлит, 1973. |
|
|
3. Лунгу К.Н. Сборник задач по высшей математике / К.Н.
Лунгу, Д.Т. Письменный. – М.: Рольф, 2007.
4. Письменный Д.Т. Конспект лекций по высшей математике: Полный курс / Д.Т. Письменный. – М.: Айрис-
пресс, 2008.
5. Данко П.Е. Высшая математика в упражнениях и
задачах / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. – М.:
Высш. шк., 1998.
6.Минорский В. П. Сборник задач по высшей математике
/В.П. Минорский. — М.: Наука, 1987.
7.Щипачев B.C. Высшая математика / В.С. Щипачев. —
М.: Высш.школа, 2003.
8. Бугров Я.С. Дифференциальное и интегральное
исчисление / Я.С. Бугров, С.М. Никольский. М.: Наука, 1984.
47
ОГЛАВЛЕНИЕ
1.Двойной интеграл и его вычисление …………………. 3
2.Двойной интеграл в полярных координатах.
Замена переменных в двойном интеграле …………….. 12
3.Вычисление площадей плоских фигур и площади поверхности ……………………………………16
4.Вычисление объемов тел …………………………… ….23
5.Приложения двойного интеграла к механике ………. 27
6.Тройной интеграл ………………………………………. 32
7.Вычисление величин посредством тройного интеграла …………………………………………………40
БИБЛИОГРАФИЧЕСКИЙ СПИСОК……………………. 47
48
КРАТНЫЕ ИНТЕГРАЛЫ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ для организации самостоятельной работы
по курсу "Высшая математика" для студентов направления 20.01.03 "Техносферная безопасность"
(направленности «Защита в чрезвычайных ситуациях», «Безопасность жизнедеятельности в техносфере», «Защита окружающей среды»)
очной формы обучения
Составитель: Пантелеев Игорь Николаевич
В авторской редакции
Компьютерный набор И.Н. Пантелеева
Подписано к изданию 21.11.2016.
Уч.- изд. л. 3,1
ФГБОУ ВО «Воронежский государственный технический университет»
394026 Воронеж, Московский просп., 14
49
