
Учебное пособие 707
.pdf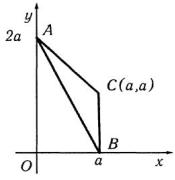
|
|
|
|
|
Рис. 21 |
|
|
|
|
|
|
||||
Уравнение |
прямой AB : |
x |
+ |
y |
=1 |
|
или y = 2 (a - x); |
||||||||
|
2a |
|
|||||||||||||
|
x - a |
|
|
y - a |
|
|
a |
|
|
|
|
|
|||
прямой AC : |
= |
или y = 2a - x . |
|
|
|
|
|||||||||
-a |
|
|
|
|
|
||||||||||
|
|
|
a |
|
|
|
|
|
|
|
|
|
|||
Момент инерции по формуле (4) |
|
|
|
|
|
||||||||||
|
|
2 |
|
|
a 2 |
|
2a -x |
a |
3 |
|
a4 |
||||
I y = òòx |
dxdy = òx |
dx ò |
dy = òx dx = |
|
. |
||||||||||
4 |
|||||||||||||||
|
S |
|
0 |
|
2(a-x ) |
0 |
|
|
|
||||||
5.4. Определить моменты инерции Ix , I y , I0
прямоугольной пластинки, ограниченной линиями х = 0, х = а, у = 0 и у = b, если плотность ее в каждой точке равна квадрату расстояния точки от начала координат.
Решение. Учитывая, что поверхностная плотность
пластинки |
в |
точке d (x, y ) = x2 + y2 , по |
формулам (4) будем |
||||||||||
иметь |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
b |
|
|
|
Ix |
= òò(x2 + y2 ) y2dxdy = òdxò(x2 y2 + y4 )dy = |
||||||||||||
|
|
S |
|
|
|
|
|
|
0 |
0 |
|
|
|
|
a æ |
|
2 b3 |
|
b5 |
ö |
3 |
æ a2 |
|
b2 |
ö |
||
= |
ç x |
|
|
+ |
|
÷ dx = ab |
|
ç |
|
+ |
|
÷. |
|
|
|
|
|
|
|
||||||||
|
ò0 è |
|
3 |
|
5 |
ø |
|
è 9 |
|
5 |
ø |
||
31
a b
I y = òò(x2 + y2 )x2dxdy = òdxò(x4 + y2 x2 )dy =
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
æ 4 |
|
|
|
b3 |
|
2 |
ö |
|
3 |
æ a2 |
|
b2 |
ö |
|
|
|
|
|
|
||||||||
|
= |
|
ç x |
b + |
|
|
|
x |
|
÷dx = a b ç |
|
|
+ |
|
|
|
÷. |
|
|
|
|
|
|||||||||
|
|
3 |
|
|
5 |
|
9 |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
ò0 è |
|
|
|
|
|
|
ø |
|
|
è |
|
|
|
ø |
|
|
|
|
|
|
||||||||
I0 = òò(x2 + y2 )2 |
|
|
|
a |
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
dxdy = òdxò(x4 + 2x2 y2 + y4 )dy = |
|||||||||||||||||||||||||||||||
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
æ |
|
4 |
|
|
2 |
|
2 |
|
|
3 |
|
|
b5 |
ö |
|
|
æ a4 |
|
|
|
2 |
2 |
|
2 |
|
b4 ö |
|||
= |
|
ç x |
|
b + |
|
x |
b |
|
+ |
|
|
÷ dx |
= ab ç |
|
|
|
+ |
|
|
a |
b |
|
+ |
|
÷. |
||||||
|
|
3 |
|
5 |
|
|
|
|
|
|
|
||||||||||||||||||||
|
ò0 è |
|
|
|
|
|
|
|
|
|
|
ø |
|
|
è |
|
5 9 |
|
|
|
|
5 ø |
|||||||||
6. Тройной интеграл
1°. Тройной интеграл является обобщением понятия двойного интеграла на случай функции трех переменныхf(x,y,z) и представляет конечный предел трехмерной интегральной суммы в области V
òòò
(V )
где
f (x, y, z )dxdydz |
= |
max Dx ®0 ååå ( |
i j |
k ) |
D |
i |
D |
|
j |
D |
k |
(1) |
|||
|
lim |
|
|
f |
x , y , z |
|
x |
|
y |
|
|
z , |
|
||
|
|
i |
i |
j k |
|
|
|
|
|
|
|
|
|
|
|
|
|
max Dy j ®0 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
max Dzk ®0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Dxi Dy j Dzk = (xi+1 - xi )(y j +1 - y j )(zk +1 - zk ) |
- |
объем |
элемен- |
||||||||||||
тарных областей, на которые разбивается пространственная область V.
Для непрерывной в областиV функции f(x,y,z) предел (1) существует и не зависит от способа разбиения области Кна элементарные области объемом Dxi Dy j Dzk , от выбора точки в
каждом элементарном объеме, в которой вычисляется f(x,y,z), и от способа стремления наибольшего диаметра элементарной области к нулю.
Основные свойства тройных интегралов аналогичны свойствам двойных интегралов.
32
2°. Вычисление тройного интеграла сводится к последовательному вычислению трех обыкновенных определенных интегралов
|
x2 |
y2 (x) |
z2 (x, y ) |
|
òòò f (x, y, z )dxdydz = ò dx |
ò dy |
ò f (x, y, z )dz . |
(2) |
|
V |
x1 |
y1(x ) |
z1(x , y ) |
|
Если внутренний интеграл берется по переменной z, то переменные (х, у) при интегрировании его рассматриваются как постоянные величины. Пределы интегрирования во внутреннем интеграле, как правило, являются переменными и зависят от (х, у). Таким образом, задача сводится к вычислению двойного интеграла, у которого пределы интегрирования внутреннего интеграла в общем случае зависят от переменнойх, а пределы интегрирования внешнего интеграла постоянны.
3°. Пусть в тройном интеграле требуется от переменных х, у, z перейти к переменным u, v, w, связанным соотношениями
x = x (u, v, w), y = y (u, v, w), z = z (u,v, w ) . |
(3) |
Функции (3) осуществляют взаимно-однозначное и непрерывно дифференцируемое отображение областиG пространства Ouvw на область V пространства Oxyz. Если якобиан этого отображения
|
¶x |
|
|
¶x |
|
|
¶x |
|
|
|
¶u |
|
|
¶v |
|
|
¶w |
|
|
I = |
¶y |
|
|
¶y |
|
|
¶y |
|
¹ 0 |
¶u |
|
|
¶v |
|
|
¶w |
|||
|
|
|
|
|
|
||||
|
¶z |
|
|
¶z |
|
|
¶z |
|
|
|
¶u |
|
|
¶v |
|
|
¶w |
|
|
не обращается в нуль наG и функция f(x,y,z) непрерывна в области V, то справедлива формула
33
òòò f (x, y, z )dxdydz =
V |
|
|
( |
|
|
|
|
|
|
|
)) |
(4) |
|
|
òòò |
|
|
( |
|
) |
( |
) |
( |
||||
= |
|
f |
|
x |
|
u, v, w |
|
, y u, v, w |
|
, z u,v, w |
|
I |
dudvdw. |
G
Производить замену переменных по формулам (3) следует в том случае, если область интегрирования G в интеграле (4) значительно проще области V.
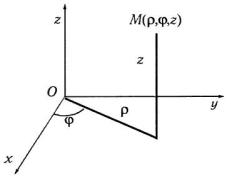
Если при вычислении тройного интеграла целесообразнее перейти от переменных х, у, z к цилиндрическим координатам r,j, z (рис. 22), связанным с декартовыми координатами соотношениями
x = r cosj, y = r sin j, z = z
(0 £ r < +¥, 0 £ j £ 2p , - ¥ < z < +¥) ,
где якобиан преобразования равен |
|
|
|
|||
I = |
|
cosj |
-r sinj |
0 |
|
= r , |
|
|
|||||
|
sin j |
r cosj |
0 |
|
||
|
|
0 |
0 |
1 |
|
|
то формула преобразования имеет вид
òòò f (x, y, z )dxdydz = òòò f (r cosj, r sin j, z )rd rdjdz . (5)
V G
Рис. 22
34
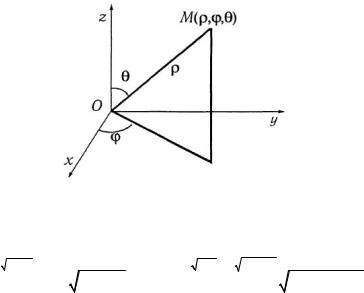
В случае перехода от декартовых координатх, у, z к сферическим координатам r,j,q (рис. 23), связанным с x,y,z
соотношениями |
x = r sinq cosj, y = r sinq sin j, z = r cosq |
|||||
(0 £ r < +¥, 0 £ j £ 2p, 0 £q £ p ) , |
где якобиан преобразо- |
|||||
вания равен |
|
|
|
|
||
I = |
|
sinq cosj |
-r sin q sin j |
r cosq cosj |
|
= r 2 sin q , |
|
|
|||||
|
sinq sin j |
r sinq sin j |
r cosq sin j |
|
||
|
|
cosq |
0 |
-r sinq |
|
|
формула преобразования тройного интеграла имеет вид
òòò f (x, y, z )dxdydz =
V |
(6) |
|
= òòò f (r sin q cosj, r sin q sin j, r cosq )r2 sin qdpdjdq. |
||
|
||
G |
|
Рис. 23
1 x y
6.1. Вычислить следующие интегралы: а) òdxòdyò xyzdz ;
|
|
|
|
|
0 |
0 |
0 |
2 |
2 x-x2 |
a |
1 |
1-x2 |
1-x2 - y2 |
|
|
б) òdx ò dyò z x2 + y2 dz ; в) òdx ò dy ò |
x2 + y2 + z2 dz . |
||||||
0 |
0 |
0 |
0 |
0 |
0 |
|
|
Решение. а) Вычисление тройного интеграла начинается с
35

вычисления внутреннего интеграла. Полагая х и у постоянными, интегрируем по z, тогда получим
1 |
x |
z |
2 |
|
I = òdxòxy |
|
|||
2 |
||||
0 |
0 |
|||
|
y |
|
1 |
1 |
x |
|
|
||||
|
|
dy = |
òdxò xy3dy . |
||
|
|
|
|||
|
0 |
2 |
0 |
0 |
|
|
|
|
|||
Таким образом, тройной интеграл свелся к двойному. Вычисляем теперь двойной интеграл
|
1 |
1 |
y |
4 |
|
x |
|
1 |
1 |
1 |
|
|
|
|
|
|
|||||||||
I = |
ò x |
|
|
|
|
dx = |
òx5dx = |
. |
||||
|
4 |
|
|
|
|
48 |
||||||
2 |
0 |
|
|
0 |
8 |
0 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|||
б) Данный интеграл следует вычислять в цилиндрической системе координат. Однако, целесообразнее сначала найти внутренний интеграл по z, а затем перейти к полярной системе координат
2 |
2 x-x2 |
|
z |
2 |
|
a |
|
a |
2 2 |
2x-x2 |
|
|
|
|
|
|
|
||||||||
I = òdx ò |
x2 + y 2 |
|
|
|
dy = |
|
òdx |
ò |
x 2 + y 2 dy . |
|||
|
|
|
|
|
|
|||||||
0 |
0 |
2 |
|
0 |
2 |
0 |
0 |
|
||||
|
|
|
|
|
|
|
|
|||||
Область интегрирования последнего интеграла показана на рис. 24. Переходя к полярным координатам x = r cosj ,
y = r sinj , будем иметь
|
|
|
p |
2cosj |
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
p |
|||||||
|
a |
2 |
|
2 |
|
|
|
|
|
8a |
2 |
|
|
2 |
|
|
|
|
|
|
|
4 |
|
2 |
|
|
I = |
|
|
òdj |
ò r 2d r = |
|
|
|
òcos3 jdj = |
a2 ò(1- sin2 j )d sinj = |
|||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||
2 |
0 |
|
0 |
|
|
|
6 |
|
0 |
|
|
|
|
|
|
|
3 |
|
0 |
|
||||||
|
|
|
|
|
|
|
4 |
|
|
æ |
|
|
1 |
|
|
ö |
|
p |
8 |
|
|
|
||||
|
|
|
|
|
|
|
|
2 |
|
|
|
3 |
|
2 |
|
2 |
|
|
||||||||
|
|
|
|
|
|
= |
|
a |
|
çsin j - |
|
|
|
|
sin |
|
j ÷ |
|
= |
|
a |
. |
|
|||
|
|
|
|
|
|
3 |
|
3 |
|
9 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
è |
|
|
|
|
ø |
|
0 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
36
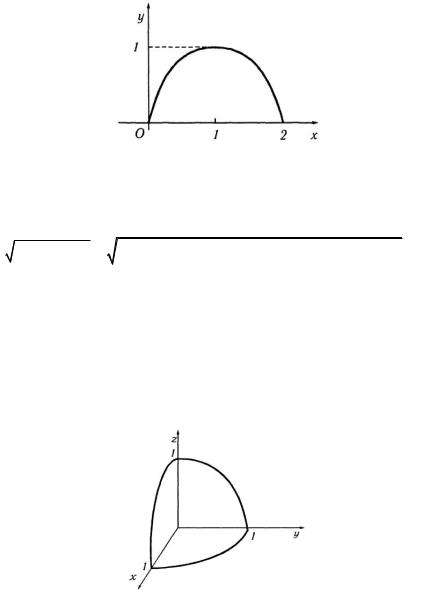
Рис. 24 в) Представим область интегрирования на рис. 25. Не-
трудно заметить, что она займет первый октант единичного шара. Переходя к сферической системе координат, подынтегральная функция будет равна
x2 + y2 + z2 = (r sin q cosj )2 + (r sin q sin j )2 + (r cosq )2 = r
Таким образом, пользуясь формулой (6) и расставляя пределы интегрирования, будем иметь
pp
2 |
|
2 |
1 |
I = òòòr × r2 sinqd rdjdq = òsinqdq òdjòr3d r =
G |
|
|
|
|
|
0 |
0 0 |
|||||
|
p |
p |
|
p |
|
|
|
|||||
= 1 |
2 |
|
2 |
|
p |
|
2 |
|
|
p |
|
|
òsinqdq òdj = |
|
òsin q dq = |
. |
|||||||||
8 |
|
|||||||||||
4 |
0 |
|
0 |
|
0 |
|
8 |
|
||||
Рис. 25
37
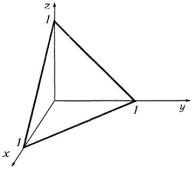
6.2. Вычислить интегралы: a) òòòV |
|
dxdydz |
|
, |
где V - |
|
|||
(x + y + z +1)3 |
|
||||||||
область, ограниченная |
координатными |
плоскостями |
и |
||||||
плоскостью |
x + y + z =1 ; |
б) òòòdxdydz , |
где V |
– |
область |
|
|||
|
|
|
V |
|
|
|
|
|
|
ограниченная |
поверхностями x2 + y2 + z2 |
= 2Rz, x2 + y2 = z2 и |
|
||||||
содержащая |
точку (0, 0, R); |
в) òòò zdxdydz где V - |
область, |
|
|||||
|
|
|
V |
|
|
|
|
|
|
ограниченная конусом x2 + y2 |
= z2 т плоскостью z = h . |
|
|||||||
Решение. а) Область интегрирования показана на рис. 26. |
|
||||||||
Рис. 26 Расставим пределы интегрирования
|
dxdydz |
1 |
1-x |
|
I = òòò |
|
= òdx ò dy |
||
(x + y + z +1) |
3 |
|||
V |
0 |
0 |
||
Полагая х и у постоянными внутренний интеграл по z
1-x- y |
dz |
||
ò0 |
|||
|
. |
||
(x + y + z +1)3 |
|||
величинами, вычисляем
38

|
|
|
1 |
1 1-x |
|
1 |
|
|
1-x- y |
|||
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
||||||
I = - |
|
ò0 dx ò0 |
|
|
|
|||||||
2 |
(x + y + z +1)2 |
0 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
1-x æ 1 |
|
1 |
ö |
||||
|
|
|
ò |
|
ò |
ç |
|
|
|
2 ÷ |
||
= - |
|
|
|
dx |
|
ç |
|
- |
|
|
÷dy |
|
|
2 0 |
|
0 |
è 4 |
|
(x + y +1) |
ø |
|||||
dy =
|
1 1 |
æ y |
|
1 |
|
ö |
|
1-x |
||
|
|
|
|
|||||||
= - |
+ |
|
|
dx = |
||||||
|
|
ç |
|
|
|
÷ |
|
|||
2 |
|
4 |
x + y +1 |
|||||||
|
ò0 è |
|
ø |
|
0 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
1 1 æ |
1 |
(1- x)+ |
1 |
|
|
1 ö |
1 æ |
|
5 |
|
ö |
|
|||||
= - |
|
ç |
|
|
|
|
- |
|
÷ dx = |
|
çln 2 |
- |
|
|
|
÷. |
|
|
2 |
4 |
2 |
|
|
|
8 |
|
|
||||||||||
|
ò0 è |
|
|
x +1 ø |
2 è |
|
|
ø |
|
|||||||||
б) |
|
|
Преобразуя |
|
|
уравнение |
|
|
|
сферы |
к |
|||||||
x2 + y2 + (z - R)2 = R2 , |
нетрудно |
заметить, |
что центр |
сферы |
||||||||||||||
смещен по оси z на R. Таким образом, область интегрирования ограничена сверху сферической, а снизу конической поверхностью (рис. 27). Искомый интеграл в сферической системе координат примет вид
I = òòòdxdydz = òòòr2 sinqd rdqdj .
V G
Рис. 27 Подставляя в уравнение сферы сферические координаты,
будем |
иметь r = 2R cosq . |
Расставляя |
пределы |
интегрирования, получим |
|
|
|
39

|
|
|
|
p |
|
|
|
|
|
p |
|||
|
2p |
|
|
4 |
|
|
2 R cosq |
8R |
3 2p |
|
4 |
|
|
I = ò dj òsinq dq ò r 2 dr = |
|
ò dj òcos3 q sin q dq = |
|||||||||||
3 |
|
||||||||||||
0 |
|
0 |
|
|
0 |
0 |
0 |
|
|||||
|
8R |
3 |
|
|
|
p |
2p |
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|||
= - |
|
cos4 q |
|
ò dj = p R3 . |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||||||
3×4 |
|
|
|
0 |
0 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||||
в) Проекция конуса на плоскость Оху есть круг х2 + у2 = h2 (рис. 28). Расставляя пределы интегрирования в тройном интеграле, будем иметь
|
h |
1 |
2p æ |
r |
2 |
|
r |
4 |
ö |
|
h |
4 |
|
|
|
|
|
|
|||||||||||
I = òòdxdyò(h2 - p2 )rd r = |
ò ç h2 |
|
- |
|
÷ |
|
|
= |
h p |
. |
||||
2 |
2 |
|
|
|
||||||||||
S |
0 |
0 è |
4 |
ø |
|
0 |
4 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||
Рис. 28
7. Вычисление величин посредством тройного интеграла
1°. Объем тела, занимающего область V, в декартовой си-
стеме координат определяется по формуле |
|
V = òòòdxdydz . |
(1) |
V |
|
Масса тела, занимающего область V, определяется |
по |
формуле |
|
m = òòòd (x, y, z )dxdydz , |
(2) |
где d (x, y, z ) - плотность тела в точке (x,y,z). |
|
40
