Учебное пособие 707

a > b, a > b .

Решение. а) При вычислении площади, ограниченной астроидой, переходим к обобщенным полярным координатам

x = r cos3 j, y = r sin3 j и вычисляем якобиан

= 3r (cos4 j sin2 j + cos2 j sin 4 j ) = 3r sin 2 j cos 2 j.

Площадь, расположенная в первом квадранте, согласно формуле (3) будет равна

Таким образом S = p p a2 . 8

б) Введем новые переменные u, v по формулам xy = u2 ,

b £ v £ a . Согласно формуле (3) площадь будет равна

21

Часть конуса, расположенная в первом октанте, проектируется на четверть круга, ограниченного окружностью х2 + у2

Перейдем к полярным координатам x = r cosj, y = r sinj , тогда

22

4. Вычисление объемов тел

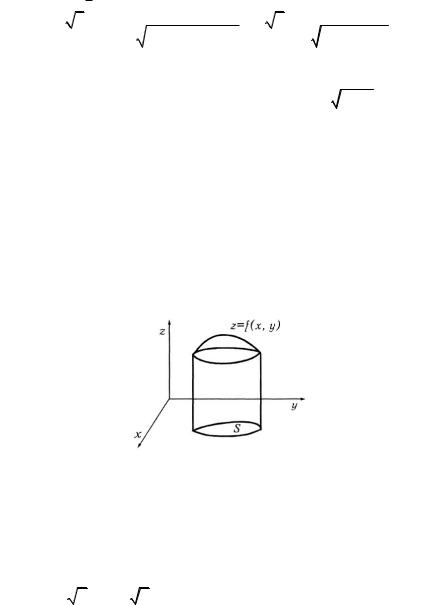
Объем цилиндрического тела, ограниченного сверху непрерывной поверхностью z = f(x,y), снизу плоскостью z = 0 и с боков цилиндрической поверхностью, вырезающей на плоскости Оху область S (рис. 14), равен

V = òò f (x, y )dxdy .

S

Рис. 14 В ряде случаев вычисление объемов цилиндрических тел

более сложной формы целесообразнее представлять в виде суммы (разности) объемов нескольких тел.

4.1. Найти объем тела, ограниченного поверхностями:

а) z2 = xy, x = a, x = 0, x = a, y = 0;

б) y = x, y = 2 x, x + z = 3, z = 0;

23

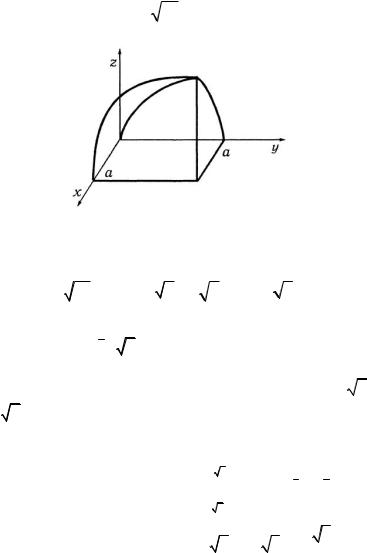
Решение.а)Тело, объем которого требуется найти, ограничено

сверху поверхностью z = xy , с боков плоскостями x = a , y = a . Половина тела показана на рис. 15.

Рис. 15 Рассматривая это тело как цилиндрическое, его объем по

формуле (1) будет

б) Данное тело с боков ограничено цилиндрами y = x и

y = 2 x , сверху плоскостью х + z = 3, снизу плоскостью z = 0 (рис. 16). Поскольку тело цилиндрическое, то для нахождения его объема воспользуемся формулой (1)

24

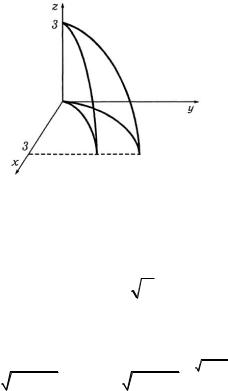
Рис. 16

4.2. Вычислить объем тела, ограниченного поверхностями:

а) x2 + y2 = R2 , x2 + z2 = R2 ;

б) z2 - x2 = a2 , z2 - y2 = a2 , z = a 2;

Решение. а) Тело ограничено двумя пересекающимися цилиндрическими поверхностями. Для нахождения его объема рассмотрим восьмую часть (рис. 17). Тогда объем равен

25

Рис. 17 б) Тело ограничено двумя пересекающимися гиперболи-

ческими цилиндрами и плоскостьюz = a 2 (рис. 18). Для нахождения объема рассмотрим четвертую часть. Проектируя на плоскость Oyz, будем иметь

Рис. 18

26

S

где d (x, y ) - поверхностная плотность пластинки в точке

(x, y ) .

2°. Статические моменты пластинки относительно координатных осей Ох и Оу вычисляются по формулам

Координаты центра тяжести пластинки

где т - масса пластинки.

3°. Моменты инерции пластинки относительно координатных осей и начала координат определяются по формулам

S

Момент инерции I0 , равный произведению массы на квад-

27

рат расстояния до полюса, принято называть полярным моментом инерции.

Если пластинка однородна, то в приведенных формулах следует положить d (x, y ) =1 .

4°. Для однородного цилиндрического тела с образующей, параллельной оси Oz, ограниченного поверхностью z = z(x, у), которая проектируется на плоскостьОху в область S, статические моменты относительно координатных плоскостей определяются по формулам

где m = òò zdxdy - масса цилиндрического тела.

S

5°. Моменты инерции однородного цилиндрического тела относительно координатных плоскостей находятся по формулам

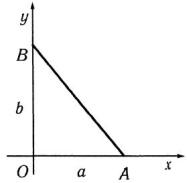
5.1. Найти массу пластинки, имеющей форму прямоугольного треугольника с катетамиOA = a и OB = b , если плотность ее в любой точке пропорциональна расстоянию точки от катета ОВ.

Решение. Запишем уравнение прямойАВ, воспользовавшись уравнением прямой в отрезках на осях

28

Пользуясь формулой (1), находим, что масса пластинки (рис. 19) будет

где к - коэффициент пропорциональности.

29

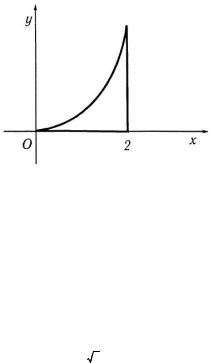
Рис. 20 По формулам (2) находим статические моменты относи-

тельно координатных осей

Координаты центра тяжести по формулам (3) будут

5.3. Найти момент инерции относительно оси Оу площади треугольника с вершинами А (0, 2a ), B (a, 0) и С (a, a ).

Решение. Покажем треугольник на рис. 21.

30