Учебное пособие 598
.pdf
ФГБОУ ВО «Воронежский государственный технический университет»
Кафедра высшей математики и физико-математического моделирования
209-2016
КРИВОЛИНЕЙНЫЕ И ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ для организации самостоятельной работы
по курсу «Высшая математика» для студентов направления 20.01.03 «Техносферная безопасность»
(направленности «Защита в чрезвычайных ситуациях», «Безопасность жизнедеятельности в техносфере», «Защита окружающей среды»)
очной формы обучения
Воронеж 2016
Составитель канд. физ.-мат. наук И.Н. Пантелеев |
|
|
|||
УДК 51 (075) |
|
|
|
|
|
Криволинейные |
и |
поверхностные |
: интеграл |
||
методические |
указания |
для |
организации самостоятельной |
||
работы по |
курсу«Высшая |
математика» для |
студентов |
||
направления |
20.01.03 |
«Техносферная |
безопасность» |
||
(направленности |
«Защита |
в |
чрезвычайных |
|
ситуациях», |
«Безопасность |
жизнедеятельности в техносфере», |
«Защита |
|||
окружающей среды») очной формы обучения / ФГБОУ ВО «Воронежский государственный технический университет»; сост. И.Н. Пантелеев. Воронеж, 2016. 45 с.
Методические указания предназначены в качестве руководства для организации самостоятельной работы по курсу "Высшая математика" по разделу «Теория поля» для студентов направления 20.01.03 «Техносферная безопасность» в 3 семестре. В работе приведен теоретический материал,
необходимый для выполнения заданий и решение типовых примеров.
Методические указания подготовлены в электронном виде и содержатся в файле Vmfmm_ KrPvInT _16.pdf.
Ил. 31. Библиогр.: 4 назв.
Рецензент канд. физ.-мат. наук, проф. Г.Е. Шунин Ответственный за выпуск зав. кафедрой д-р физ.-мат. наук, проф. И.Л. Батаронов
Издается по решению редакционно-издательского совета Воронежского государственного технического университета
Ó ФГБОУ ВО «Воронежский государственный технический университет», 2016
1. КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ ПО ДЛИНЕ ДУГИ ( I рода)
Опорный конспект № 1
1) Понятие КИ 1p
О: f (x, y ) |
непр. в D , |
AB Ì D , AB |
|||||||||||||||
разбивается на Ai-1 Ai |
длиной Vli , |
||||||||||||||||
i = |
|
, M1 (xi , ni )ÎVli Þ |
|
|
|||||||||||||
1, n |
|
|
|||||||||||||||
ò f (x, y dl) |
|
|
|
|
|
n |
|
|
)Vli . |
||||||||
= |
lim |
|
å f (xi , ni |
||||||||||||||
|
|
|
|
|
|
|
maxVli ®0 i=1 |
|
|
» |
|||||||
p (x, y ) - линейная плотность |
|||||||||||||||||
AB Þ |
|||||||||||||||||
m = ò f (x, y )dl |
- масса AB |
|
|
||||||||||||||
2) Свойства КИ 1p |
|
|
|
|
|
||||||||||||
1°. |
|
ò ( f1 (x, y)+ f2 (x, y ))dl = ò |
f1dl + ò f2dl ; |
||||||||||||||
|
» |
|
|
|
|
|
|
|
|
|
|
|
» |
» |
|||
|
|
AB |
|
|
|
|
|
|
|
|
|
|
|
AB |
AB |
||
2°. |
|
ò cf (x, y )dl = c ò |
f (x, y )dl , |
c = const ; |
|||||||||||||
|
» |
|
|
|
|
|
|
|
|
» |
|
|
|
|
|
||
|
|
AB |
|
|
|
|
|
|
|
|
AB |
|
|
|
|
||
3°. L = L1 + L2 Þ ò f (x, y )dl =ò fdl + ò fdl ; |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
L1 |
L2 |
||
4°. òdl = l |
- длина L ; |
|
|
|
|
||||||||||||
|
|
L |
|
f (x, y )dl = ò |
f (x, y )dl |
|
|
||||||||||
5°. |
ò |
|
|
|
|||||||||||||
|
» |
|
|
|
|
|
|
» |
|
|
|
|
|
|
|||
|
|
AB |
|
|
|
|
|
|
BA |
|
|
|
|
|
|
||
3) Вычисление КИ 1p |
|
|
|
||||||||||||||
a) |
» |
|
|
|
|
y = y (t ) - непр. дифф. на [a, b ] Þ |
|||||||||||
|
AB : x = x (t ), |
||||||||||||||||
|
ò |
|
|
( |
|
) |
|
b |
|
( |
|
( |
) ( |
)) |
|
||
Þ |
f |
|
= |
ò |
f |
x |
x 2 + y 2 dt ; |
||||||||||
|
|
|
x, y dl |
|
|
|
t , y t |
|
|||||||||
|
» |
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
||
|
AB |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3
|
|
|
b) |
» |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
AB : y = y (x )- непр. дифф. на [a, b] Þ |
||||||||||||||||||||||||||
|
ò ( |
|
) |
|
b |
|
( |
|
|
( )) |
|
|
( |
|
( )) |
2 |
|
|
|
|
|
||||||||
|
|
|
ò |
|
|
|
|
|
¢ |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Þ f x, y dl = |
|
f x, y x |
|
|
1+ y |
|
|
x dx . |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
» |
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
AB |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вычисление криволинейного интеграла I рода |
|||||||||||||||||||||||||||||
Криволинейный |
|
интеграл |
ò f (x, y)dl |
|
легко сводится к |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
» |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
AB |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
определенному интегралу. Примем за параметр длину дуги l , |
|||||||||||||||||||||||||||||
отсчитываемую |
от |
|
|
точкиA |
|
|
по |
|
|
|
|
|
|
|
|
» |
получим |
||||||||||||
|
|
|
|
|
|
|
|
кривойAB , |
|||||||||||||||||||||
параметрическое |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
представление |
||||||||||||
» |
= x (l ), |
y = y (l ), 0 £ l £ l |
* |
, |
где |
|
l |
* |
|
|
– |
|
длина |
» |
|||||||||||||||
AB : x |
|
|
|
|
|
|
дуги AB . |
||||||||||||||||||||||
Пусть |
|
промежуточным |
точкам M i |
(xi ,hi ) |
|
соответствует |
|||||||||||||||||||||||
l = li* , т.е. xi = x (li* ) , hi |
= y (li* ). Тогда |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
n |
|
|
|
|
i |
|
i |
|
n |
|
|
|
|
( i |
|
) |
|
i |
(û )i |
|
||||
|
|
|
|
|
å i |
|
|
|
å ë |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
f (x ,h )Dl = |
|
|
f |
é |
x l |
* |
, y l |
* |
ù |
Dl |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Последняя сумма является интегральной для определения |
|||||||||||||||||||||||||||||
|
|
|
l* |
|
ë |
), y |
l( |
û |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
интеграла |
ò |
f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
éx (l |
ù)dl , т.е. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ò |
f (x, y |
|
dl) |
|
|
l* |
ë |
|
|
|
|
|
|
|
û |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
= |
ò |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.1) |
||||||||
|
|
|
|
|
|
|
f éx (l ), y l( |
ù)dl . |
|
|
|
|
|||||||||||||||||
|
|
|
|
» |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
AB |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Эта формула доказывает существование криволинейного |
|||||||||||||||||||||||||||||
интеграла I |
рода от функции f (x, y ), |
непрерывной в D , если |
|||||||||||||||||||||||||||
»AB Ì D – непрерывная кусочно-гладкая кривая.
Рассмотрим формулы для вычислений криволинейного
интеграла в следующих случаях: |
|
|
a) |
» |
(t ), a £ t £ b , где x (t ) и y (t ) |
AB : x = x (t ), y = y |
||
непрерывно дифференцируемые на [a, b ], тогда |
||
dl = |
(x¢(t ))2 + (y¢(t ))2 dt |
т.е. из (1.4) имеем |
4
b
ò f (x, y dl) = ò
» |
a |
AB |
|
Формула может случай, т.е. если
ë ( ) |
( û) ( |
¢ |
( )) |
2 |
|
( |
|
¢ |
( )) |
2 |
||
f éx t , y t ù x |
|
t |
|
|
+ |
|
y |
t dt . |
||||
|
|
|
|
|
|
|||||||
быть |
обобщена |
|
на |
|
пространственный |
|||||||
» |
|
|
|
|
|
|
(x, y, z ) |
непрерывна |
||||||||
AB : x = x (t ), y = y (t ), z = z (t ),a £ t £ b, f |
||||||||||||||||
в D , |
» |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
AB Ì D , тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
b |
)( |
|
|
( )) |
2 |
( |
|
( )) |
2 |
( |
|
( )) |
2 |
ò ( |
) ò ë ( ) ( ) (û |
|
¢ |
¢ |
¢ |
|||||||||||
|
|
|
|
|||||||||||||
|
f x, y dl = f éx t , y t , z t ù |
|
x |
t |
|
+ y |
t |
|
+ z |
t dt |
||||||
|
|
|
|
|
|
|
||||||||||
» |
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
AB |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Аналогично записывается формула для большего числа переменных.
Пример. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
ò(x2 + y2 )dl = ? |
L : x = a cos t, y = a sin t, 0 £ t £ 2p |
||||||||||||||||
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2p |
|
|
|
|
|
|
|
|
|
|
|
|
|
ò(x2 + y2 )dl = ò (a2 cos2 t + a2 sin2 t ) |
a2 sin2 t + a2 cos2 tdt = |
||||||||||||||||||
L |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= a3 ò dt = 2pa3 . |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
b) |
» |
|
|
|
|
|
|
|
|
где y (x ) непрерывно |
|||||
|
|
|
|
AB : y = y (x ), a £ x £ b , |
|
||||||||||||||
|
дифференцируема на [a, b] , тогда |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
dl = 1+ (y¢(x ))2 dx |
|
|
|
||||||||
|
ò ( |
|
|
) |
2p |
|
|
|
( )û |
|
( |
|
|
( )) |
2 |
||||
|
|
|
ò ë |
|
|
|
¢ |
||||||||||||
|
|
|
|
|
|
|
|||||||||||||
и f x, y dx = |
|
|
|
f éx, y x ù 1 + |
|
y |
|
x dx . |
|||||||||||
|
|
|
|
|
|
||||||||||||||
|
» |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
AB |
|
|
|
|
|
|
|
|
|
массу кривойy = ln x,1 £ x £ 2 , если |
||||||||
Пример. |
Найти |
|
|||||||||||||||||
линейная плоскость r (x, y ) = x2 . |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
m = ò x2dl = ò x |
1+ x2 dx = 0,5ò(1+ x2 )1/ 2 d (1+ x2 )= |
||||||||||||||||||
|
|
AB |
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
» |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 0,5 × |
2 |
(1+ x2 )3/ 2 |
|
12 |
= |
1 |
(5 5 - 2 |
2 ). |
|
|
|
|
|||||||
|
|
|
|
|
|||||||||||||||
3 |
|
3 |
|
|
|
|
|||||||||||||
5
2. КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ
(II РОДА)
Опорный конспект №2
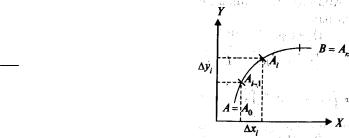
1) Определение КИ 2р. Задача о работе
r |
|
|
a = {P (x, y ),Q (x, y )} |
|
|
P (x, y ),Q (x, y ) - |
непр. в D , |
|
» |
» |
разбивается |
AB Ì D . |
AB |
|
Ai-1 Ai , i =1, n .
Ai-1 Ai = {Dxi , Dyi } , M (xi ,hi )Î Ai-1 Ai
rr
òa ×dr = ò Pdx + Qdy =
» |
» |
AB |
AB |
= lim |
å |
P (x |
,h |
)Dx + Q |
(x |
,h |
)Dy |
|
max Dx, y ®0 |
i |
i |
i |
|
i |
i |
i |
|
1 |
(i ) |
|
|
r |
|
|
|
|
|
|
|
r |
|
|
|
||
|
|
|
|
|
|
|
||
W = ò Pdx + Qdy = ò F ×dr - работа силы |
||||||||
» |
|
|
|
» |
|
|
|
|
AB |
|
|
|
AB |
|
|
|
|
r |
{P (x, y ), Q (x, y )} |
|
|
|||||
F = |
|
|
||||||
на »AB , drr = {dx, dy}
2) Свойства КИ 2р
1°. ò Pdx + Qdy = - ò Pdx + Qdy ;
» |
» |
AB |
BA |
( ( ( |
ò Pdx +Qdy = ò Pdx +Qdy + ò Pdx +Qdy ; |
||
2°. AB = AC +CB = |
|||
|
» |
» |
» |
|
AB |
AC |
CB |
3°. D = D1 + D2 , ¶D1 = L1 , ¶D2 = L2 , ¶D = L Þ |
|
||
Ñò Pdx + Qdy = Ñò |
+ Ñò |
|
|
L |
L1 |
L2 |
|
6
3)Вычисление КИ 2р
1)»AB : x = x (t ), y = y (t ) - непр. дифф. на [a, b ]
b
Þ ò Pdx + Qdy =ò(P (x (t ), y t( ))x¢(t )+Q (x (t ), y t( ))y¢(t ))dt
» |
a |
|
AB |
» |
|
2) |
||
AB : y = y (x )- непр. дифф. на [a, b] Þ |
b
Þ ò Pdx + Qdy =ò(P (x, y (x ))+Q (x, y (x ))y¢(x ))dx
»AB a
4) Связь между КИ 1р и 2р
LM - касательная к »AB в т. M ,
a= (L·M ,OX ), b = (L·M ,OY ),g = (L·M , OZ )Þ
Þò P (x, y, z )dx + Q (x, y, z )dy + R (x, y, z )dz =
»AB
= ò (P cosa + Q cos b + R cos g )dl
»AB
5) Формула Грина |
|
|
|
|
|
¶P |
|
¶Q |
|
|
P (x, y ),Q (x, y ) |
непр. в D вместе с |
, |
, |
|||||||
|
|
|||||||||
|
|
|
|
|
|
¶y ¶x |
||||
|
æ ¶Q |
|
¶P ö |
|
|
|
|
|||
L = ¶D Þ Ñò Pdx + Qdyòòç |
|
- |
|
÷dxdy . |
||||||
|
|
|||||||||
L |
D è ¶x |
|
¶y ø |
|
|
|
|
|||
7
6) Условия независимости КИ 2р от контура интегрирования
1. ò Pdx + Qdy = 0"L* Ì D Û
L*
(
2. ò Pdx + Qdy не зависит от AB Ì D Û
(
AB
3.Pdx + Qdy = du,u = u (x, y )Î D Û
4.¶P = ¶Q в D ¶y ¶x
7) Интегрирование полных дифференциалов
Pdx + Qdy = du Þ
|
|
|
u (x, y )= |
(x, y) |
|
|
|
|
ò Pdx + Qdy + c = |
||
|
|
|
|
(x0 , y0 ) |
|
|
|
|
x |
y |
|
|
|
= ò + ò +c = ò P (x, y dx) + òQ (x, y dy) +c |
|||
|
|
AC CB |
x0 |
y0 |
|
Вычисление криволинейного интеграла II рода |
|||||
1) Пусть |
» |
|
|
причем |
|
AB : x = x(t), y = y(t),a £ t £ b , |
|||||
x(t) , y(t) |
непрерывно дифференцируемы на [a, b], т.е. |
||||
x(t), y(t) ÎC1[a, b] . Тогда |
|
|
|
||
|
|
ò P(x, y)dx + Q(x, y)dy = |
|
||
|
|
» |
|
|
|
|
|
AB |
|
|
|
b |
|
|
|
|
|
= ò |
|
¢ |
|
¢ |
(2.1) |
(P(x(t), y(t)) x (t) + Q(x(t), y(t)) y (t))dt . |
|||||
a
8
|
|
ò P(x, y)dx = |
|
|
n |
|
|
|
|
||
Рассмотрим |
lim |
åP(xi ,hi )Vxi . |
По |
|
|||||||
|
|
» |
|
|
maxVx i ®0 i = 1 |
|
|
|
|
||
|
|
AB |
|
|
|
|
|
|
|
|
|
теореме |
Лагранжа |
|
|
|
|
¢ |
* |
* |
,ti ) . |
|
|
Vxi = x(ti ) - x(ti-1 ) = x (ti )Vti ,ti Î(ti -1 |
|
||||||||||
Выберем |
xi = x(ti* ),hi = y(ti* ) , |
тогда |
|
|
|
|
|
|
|||
|
n |
|
|
n |
|
|
|
¢ |
* |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
åP(xi ,hi )Vxi = åP(x(ti ), y(ti )) x (ti )Vti . |
|
|
||||||||
|
i =1 |
|
|
i = 1 |
|
|
|
|
|
|
|
В правой |
части |
полученного |
|
равенства– |
интегральная |
|
|||||
сумма |
для |
определенного |
|
интеграла |
от |
фун |
|||||
|
¢ |
|
|
к |
пределу |
|
приmaxVxi ® 0 , |
|
|||
P(x(t), y(t))x (t) . Переходя |
|
|
|||||||||
получаем формулу (2.1). |
|
|
|
|
|
|
|
|
|||
2) |
Пусть |
» |
задана |
|
на |
плоскости: |
|||||
AB |
|
||||||||||
y = y(x), a £ x £ b , |
причем |
y = y(x) |
– |
непрерывно |
|
||||||
дифференцируемая |
на [a,b] |
функция. |
Тогда, считаем |
|
|||||||
параметром, из (2.1) получаем |
|
|
|
|
|
|
|
||||
|
|
|
b |
|
|
|
|
|
¢ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ò P(x, y)dx + Q(x, y)dy = ò[P(x, y(x)) +Q(x, y(x)) y (x)]dx . |
|
||||||||||
» |
|
|
a |
|
|
|
|
|
|
|
|
AB |
|
|
|
|
|
|
|
ur |
|
|
|
Примеры: |
1. Найти работу |
силы |
|
по |
|
||||||
F ={-y, x, z} |
|
||||||||||
перемещению материальной точки вдоль винтовой линии L : x = a cos t, y = a sin t, z = bt, 0 £ t £ 2p
W = ò-ydx + xdy + zdz =
L
2p
= ò [-a sin t(-a sin t) + a cos t(a cos t) +btb]dt =
0
2p
= ò (a2 + b2t)dt = 2p(a2 + pb2 ).
0
9
2. Вычислить
ò (xy -1)dx + x2 ydy, A(1, 0), B(0, 2), AB» : 2x + y = 2 .
»AB
0
ò (xy -1)dx + x2 ydy = ò[x(2 - 2x) -1) + x2 (2 - 2x)(-2)]dx =
» |
1 |
AB |
|
=(x4 - 2x3 + x2 - x) 10 =1.
3.ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ Опорный конспект №3
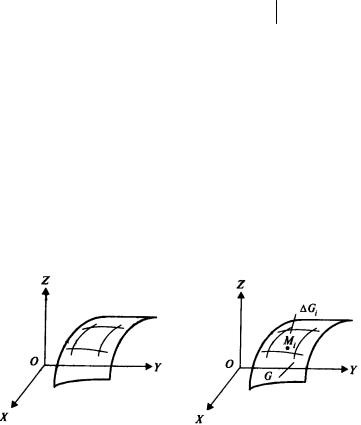
1)Поверхность в R3
G : z = z(x, y), M (x, y) Î R2 , z(x, y), z¢x , z¢y - |
непрерывны в |
|||
D Û G – |
гладкая |
поверхность, являющаяся |
двусторонней. |
|
Единичный |
|
вектор |
r |
|
|
нормалиn = {cosa, cos b, cos g}, |
|||
¶ |
¶ |
¶ |
r |
|
a = (n, i), b = (n, j),g = (n, k) , |
n(M ) - непрерывная функция |
|||
т. M
10