
Теплофизика сложных систем. учебное пособие. Коновалов Д.А
.pdf
X |
x |
; |
|
t tc2 |
; |
1 X. |
(2.24) |
|
|
|
|||||||
|
|
|
t |
t |
|
|
|
|
|
|
|
|
c1 |
c2 |
|
|
|
Таким образом, распределение температуры в стенке носит линейный характер.
Определим удельный тепловой поток через стенку:
q |
|
t |
. |
|
(2.25) |
|||||
|
|
|
||||||||
|
|
|
|
|
|
x |
|
|
|
|
Как было показано выше |
|
|
|
|
|
|
|
|
|
|
C |
dt |
|
|
tc1 |
tc2 |
. |
(2.26) |
|||
|
|
|
|
|||||||
1 |
dx |
|
|
|
|
|
|
|
||
Таким образом, |
|
|
|
|
|
|
|
|
|
|
q |
|
tc1 |
tc2 . |
(2.27) |
||||||
|
|
|
|
|
|
|
|
|
|
|
Подставляя (2.26) в (2.23) с учетом (2.22), получим |
||||||||||
t t |
|
|
q |
x. |
(2.28) |
|||||
|
|
|||||||||
|
|
c1 |
|
|
|
|
|
|
||
Отметим, что величина , |
Вт м2 |
К носит название тепловой про- |
||||||||
водимости стенки, а обратная величина |
, м2 К |
Вт - термического со- |
||||||||
противления стенки. Последнее понятие является крайне важным и определяющим в большинстве прикладных теплофизических задач.
Полученные решения легко могут быть трансформированы в зависимости для определения поля температур в многослойных стенках при заданной величине теплового потока (рис. 2.9). При стационарном режиме плотность тепло-
вого потока через все слои стенки одинакова q x 0. Таким образом,
x 0. Таким образом,
q |
1 tc1 |
tc2 ; |
|
|
|
|
|||
|
1 |
|
|
|
q |
2 tc2 |
tc3 ; |
|
(2.29) |
|
||||
|
2 |
|
|
|
|
n tcn |
|
|
|
q |
tc n 1 . |
|
||
|
n |
|
|
|
При этом каждый слой имеет свою толщину и свой коэффициент теплопроводности.
20
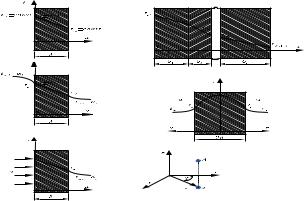
Рис. 2.9. Физическая модель задачи теплопроводности плоской многослойной стенки при граничных условиях первого рода
Выразив в каждом уравнении перепады температур в отдельном слое, сложим правые и левые части и получим выражение для определения перепада температур в многослойной стенке:
tc1 |
|
1 |
|
2 |
... |
|
(2.30) |
tc n 1 q |
|
n . |
|||||
|
|
1 |
|
2 |
|
n |
|
Сумма термических сопротивлений носит название полного термического сопротивления многослойной стенки. Из полученных соотношений возможно решение обратной задачи, т.е. определение температуры на границе каждого слоя стенки:
tc2 |
tc1 |
q |
|
1 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
1 |
|
|
|
|
|
|
|
|
tc3 |
tc1 |
q |
|
|
|
|
|
|
|
(2.31) |
|
|
|
1 |
|
2 |
; |
||||||
|
|
|
|
1 |
|
|
2 |
|
|
||
|
|
|
|
|
i |
|
|
|
|
|
|
tc i 1 tc1 q i . |
|
|
|||||||||
|
|
|
|
|
i 1 |
|
|
|
|
||
|
|
|
|
|
|
|
|
i |
|
|
|
Зачастую в прикладных задачах коэффициент теплопроводности стенки существенно различается при изменении температуры, т.е. f t . Неучет
данного фактора может существенно исказить результаты. Поэтому в таком случае расчеты корректируют, вводя линейную зависимость коэффициента теплопроводности от температуры, например 0 1 bt , где 0 – коэффициент
теплопроводности материала стенки при 0°С, b – коэффициент пропорциональности.
В этом случае, распределение температуры в стенке будет носить нелинейный характер:
21
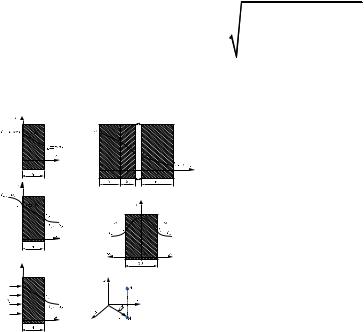
t |
1 |
2 |
|
2qx |
|
1 |
. |
(2.32) |
|
tc1 |
0b |
b |
|||||
|
b |
|
|
|
|
|
Рассмотрим решение задачи при граничных условиях третьего рода. Физическая область решения представлена на рис. 2.10.
Рис. 2.10. Физическая модель теплопроводности плоской стенки при граничных условиях третьего рода
Введем следующие допущения: -рассматривается стационарный процесс; -внутренние источники тепловыделения отсутствуют;
-теплофизические свойства стенки изотропны по всем направлениям, а значения параметров равны средним значениям;
-коэффициенты теплоотдачи к жидкости постоянны и не меняются вдоль поверхности;
-длина (или высота) стенки существенно превышает ее толщину.
Исходя из того, что удельный тепловой поток через горячую, холодную жидкость и разделяющие потоки стенку одинаков, запишем
q |
t |
|
t |
|
|
|
t |
|
t |
|
|
t |
t |
|
|
(2.33) |
||
1 |
|
ж1 |
|
c1 |
|
|
|
|
c1 |
c2 |
|
|
2 |
c2 |
|
ж2 |
|
|
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q |
|
|
|
tж1 tc1; |
|
|
|
|
|
|
||||
|
|
|
|
1 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
q |
|
|
tc1 |
tc 2; |
|
|
|
|
|
|
|
(2.34) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q |
1 |
|
tc 2 tж2 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Сложив выражения и выразив q, получим
22
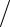
|
|
|
|
|
|
|
|
|
q |
|
tж1 |
tж2 |
|
|
(2.35) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
||||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
q k tж1 tж2 , |
|
||||||||
где k |
|
|
|
1 |
|
|
|
, Вт |
м2 К – коэффициент теплопередачи, а величина |
|||||||||
|
1 |
|
|
|
1 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
R 1 k носит название полного термического сопротивления теплопередачи. Температуры поверхности однородной стенки могут быть определены:
k носит название полного термического сопротивления теплопередачи. Температуры поверхности однородной стенки могут быть определены:
|
1 |
|
|
|
1 |
|
|
|
|
|
1 |
(2.3 |
|
tc1 tж1 q |
;tc 2 |
tж1 |
q |
|
|
tж2 |
q |
||||||
|
1 |
|
2 |
||||||||||
|
1 |
|
|
|
|
|
|
|
|||||
В случае, если стенка будет являться многослойной, то коэффициент теплопередачи будет определяться следующим выражением:
k |
|
|
1 |
|
|
|
. |
(2.37) |
|
1 |
i n |
|
1 |
|
|||
|
i |
|
|
|
|
|||
|
1 |
2 |
|
|
|
|||
|
i 1 i |
|
|
|
|
|||
По аналогии с однослойной стенкой температура на границе слоев определяется по формуле
|
|
1 |
i |
|
|
|
tc i 1 tж1 |
q |
i . |
(2.38) |
|||
1 |
||||||
|
|
i 1 |
i |
|
||
Рассмотрим смешанную задачу (рис. 2.11). С одной стороны стенки подводится тепловой поток, а с другой стороны стенка омывается теплоносителем. В данном случае с одной стороны заданы граничные условия второго рода (тепловой поток), а с другой – третьего рода.
23
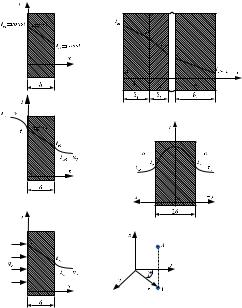
Рис. 2.11. Физическая модель теплопроводности плоской стенки при граничных условиях второго и третьего рода
Выражения для определения теплового потока запишутся в виде:
q |
|
t |
|
t |
|
|
|
t |
|
t |
|
. |
(2.39) |
c |
|
|
c1 |
|
c2 |
|
2 |
|
c2 |
|
ж2 |
|
|
Температуры стенки могут быть определены по соотношениям
|
|
1 |
|
|
|
|
|
1 |
|
(2.40) |
|
tc1 tж2 |
qc |
|
|
; |
tc 2 tж2 qc |
. |
|||||
2 |
|
|
|||||||||
|
|
|
|
|
|
2 |
|
||||
Для многослойной стенки, состоящей из n слоев, температура на поверхностях и между слоями может быть определена по формулам
t |
c n 1 |
t |
|
|
q |
1 |
; |
|
(2.41) |
||
|
|
|
|
||||||||
|
|
ж2 |
|
c |
|
|
|
||||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
2 |
|
|
|
||
|
|
|
|
|
1 |
|
i n |
|
|
|
|
tc1 tж2 |
qc |
|
|
i |
; |
(2.42) |
|||||
2 |
|||||||||||
|
|
|
|
|
i 1 |
i |
|
|
|||
|
|
1 |
i n |
|
|
|
tcт между слоями m и m 1 tж2 |
qc |
i . |
(2.43) |
|||
2 |
||||||
|
|
i m i |
|
|||
24
2.4. Передача теплоты через плоскую стенку при наличии внутренних источников тепловыделения
В ряде практически важных случаев необходимо исследование теплопроводности при наличии внутреннего источника тепловыделения. Примерами могут служить внутреннее выделение теплоты в тепловыделяющих элементах атомных реакторов, при индукционном нагреве тел, при нагреве под действием проходящего электрического тока, а также в условиях химических реакций.
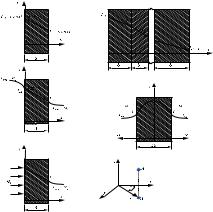
Физическая область решения представлена на рис. 2.12.
Для решения задачи введем следующие допущения:
-рассматривается стационарный процесс переноса теплоты;
-присутствуют внутренние источники тепловыделения, которые носят линейный, поверхностный или объемный характер;
-теплофизические свойства стенки изотропны по всем направлениям, а значения параметров равны средним значениям;
-коэффициенты теплоотдачи к жидкости постоянны и не меняются вдоль поверхности, охлаждение осуществляется равномерно, т.е. температура жидкости постоянна;
-длина (или высота) стенки существенно превышает ее толщину.
Рис. 2.12. Физическая модель теплопроводности плоской стенки при наличии внутренних источников тепловыделения
С учетом принятых допущений дифференциальное уравнение теплопроводности с учетом граничных условий запишется как
d 2t |
|
q |
0; |
x ; |
|
t |
tc tж . |
||
|
|
|
|
|
|
|
|||
dx |
2 |
|
|
||||||
|
|
|
|
|
x x |
|
|||
25
Вследствие симметричности области решения граничные условия могут быть записаны как
x 0; |
|
t |
0; |
|
||
|
|
|
|
|||
|
||||||
|
|
x |
|
|
|
|
|
|
|
t |
|
||
x ; |
|
tc tж . |
||||
|
|
|
||||
|
||||||
|
|
x |
|
|||
|
|
|
||||
Интегрирование исходного уравнения дает следующий результат:
dt |
|
q x |
C1;t |
q x2 |
C1x C2 , |
|
|
|
|||
|
|
|
|
||
dx |
|
|
|
2 |
|
(2.45)
(2.46)
апостоянные интегрирования определяются из граничных условий:
x; C1 0;
x ; |
C |
t |
|
|
q |
|
q |
2 |
|
|
ж |
|
V |
|
V |
. |
(2.47) |
||||
|
||||||||||
|
2 |
|
|
|
2 |
|
|
Выражение для температурного поля в любой точке пластины запишется следующим образом:
tx tж |
q |
|
q 2 |
|
|
x |
2 |
, |
(2.48) |
|
V |
|
V |
1 |
|
|
|
|
|||
|
2 |
|
||||||||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
а удельный тепловой поток составит |
|
|
|
|
|
|
|
|||
q tc tж qV . |
|
|
(2.49) |
|||||||
Следует отметить, что температура внутри стенки при наличии внутренних источников тепловыделения распределяется по параболическому закону.
При граничных условиях первого рода справедливо, что , tж tc . Температурное поле в любой точке пластины определяется выражением
t tc |
qV |
2 x2 . |
(2.50) |
|
2 |
||||
|
|
|
Температура на оси может быть вычислена по соотношению
t |
|
t |
|
|
q |
2 |
. |
|
x 0 |
c |
V |
|
(2.51) |
||||
2 |
|
|||||||
|
|
|
|
|
|
В случае линейной зависимости коэффициента теплопроводности от температуры выражение для температуры в любой точке плоской пластины при наличии внутренних источников тепловыделения может быть записано в следующем виде:
26
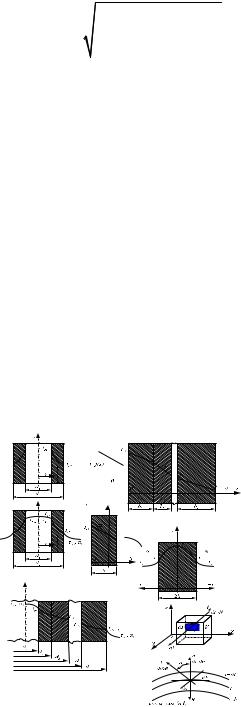
t |
1 |
|
|
|
1 |
|
2 |
q x2 |
. |
(2.52) |
b |
t0 |
b |
|
|
V |
|||||
|
|
|
|
|
|
0b |
|
|
Коэффициент теплопередачи принят постоянным в рассматриваемом интервале температур, либо его изменение носит линейный характер. На практике зачастую представлены полиномные зависимости. Также существует ряд программных комплексов для определения теплофизических характеристик различных веществ, например СТАРС, ProSim SA,а в современных математических пакетах значения определяются в любой момент времени при необходимой температуре.
2.5. Теплопроводность цилиндрической стенки
Как и в случае с плоской стенкой рассмотрим стационарный процесс теплопередачи через цилиндрическую стенку при граничных условиях первого, второго и третьего рода, а затем по аналогии перейдем к задаче с внутренними источниками тепловыделения.
Физическая область решения представлена на рис. 2.13.
Рис. 2.13. Физическая модель теплопроводности в цилиндрической стенке при граничных условиях первого рода
Введем следующие допущения:
-рассматривается стационарный процесс;
-внутренние источники тепловыделения отсутствуют;
-теплофизические свойства стенки изотропны по всем направлениям, а значения параметров равны средним значениям;
-длина (или высота) стенки существенно превышает ее толщину.
27
С учетом принятых допущений исходное уравнение теплопроводности запишем в цилиндрической системе координат:
2 |
2t |
1 t |
|
1 2t |
|
2t |
|
|
|||
t |
|
r |
|
|
|
|
|
|
|
0. |
(2.53) |
r2 |
r |
r2 |
2 |
z2 |
|||||||
Следует отметить, что температурное поле изменяется лишь в радиальном направлении, т.е. от центра к периферии. Ось 0z совпадает с осью трубы, а изотермы носят цилиндрический характер, т.е. изменения температуры вдоль угла поворота нет.
С учетом этого уравнение примет вид
d2t |
|
1 dt |
0 |
(2.54) |
|
dr2 |
r dr |
||||
|
|
|
с соответствующими граничными условиями:
r r1 |
t tc1; |
r r2 |
t tc2. |
(2.55) |
Как показано ранее, распределение поля температур по толщине стенки найдем в результате интегрирования исходного дифференциального уравнения, а константы интегрирования из соответствующих граничных условий:
|
|
|
|
|
|
dt |
|
C |
dr |
; t C lnr C ; |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
dx |
r |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
1 |
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||
при |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r r |
и t t |
|
: C |
|
tc1 tc2 |
|
; x r |
и t t |
|
: |
C |
|
t |
|
t |
|
t |
|
|
lnr1 |
|
||||||
|
|
|
|
r1 |
|
|
c2 |
|
|
|
|
|
|
||||||||||||||
1 |
|
c1 |
1 |
|
|
ln |
|
|
|
2 |
|
|
|
2 |
|
c1 |
|
c1 |
|
c2 |
|
ln |
r1 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|||
(2.56)
. (2.57)
Подставив константы интегрирования в полученное решение, получим зависимость для распределения поля температур в виде
|
|
|
|
|
|
|
ln |
r |
|
|
|
|
|
|
ln |
d |
|
|
|||
t t |
|
t |
|
t |
|
|
r1 |
|
t |
t |
t |
|
|
d1 |
. |
(2.58) |
|||||
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
c1 |
|
c1 |
|
c2 |
|
ln |
r2 |
|
c1 |
c1 |
|
c2 |
|
ln |
d2 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
d |
|
||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
Из полученного решения видно, что распределение полей температур носит нелинейный характер.
Используя закон Фурье, определим количество теплоты, передаваемое через цилиндрическую стенку. Принимая во внимание, что площадь поверхности теплообмена цилиндрической стенки F 2 rl , получим
28

Q |
2 l tc1 tc 2 |
. |
(2.59) |
|
|||
|
ln d2 |
|
|
|
d1 |
|
|
При этом плотность теплового потока может быть определена относительно внутреннего либо внешнего радиуса трубы:
q |
Q |
|
|
2 tc1 |
tc2 |
; |
(2.60) |
||||||||||
d l |
|
|
|
d2 |
|
||||||||||||
|
1 |
|
|
|
d1 ln |
|
|
|
|
|
|||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 tc1 |
|
|
d1 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
q |
|
|
Q |
|
|
|
|
tc2 |
. |
(2.61) |
|||||||
2 |
d2l |
|
d2 ln |
|
d2 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
d1 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Также общепринятым является понятие линейной плотности теплового потока, Вт/м:
q Q |
|
tc1 |
tc2 |
; q |
d q |
d q . |
(2.62) |
||||
|
|
||||||||||
l |
l |
1 |
|
|
|
l |
1 1 |
2 2 |
|
||
|
ln |
d2 |
|
|
|
||||||
|
|
|
|
2 |
d |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
1 |
|
|
|
|
В случае изменения теплопроводности материала стенки в зависимости от температуры полученное решение запишется в виде
|
|
|
|
2 |
q ln |
d |
|
|
|
|
|
|
1 |
|
|
d |
|
|
1 |
|
|
||
t |
tc1 |
|
l |
|
|
. |
|
||||
|
|
|
1 |
|
|
(2.63) |
|||||
b 0 |
|
b |
|||||||||
|
b |
|
|
|
|
|
|
|
|||
Рассмотрим решение задачи при граничных условиях третьего рода. Физическая область решения представлена на рис. 2.14.
Введем следующие допущения:
-рассматривается стационарный процесс;
-внутренние источники тепловыделения отсутствуют;
-теплофизические свойства стенки изотропны по всем направлениям, а значения параметров равны средним значениям;
-коэффициенты теплоотдачи к жидкости постоянны и не меняются вдоль поверхности
-длина (или высота) стенки существенно превышает ее толщину.
29
