
Методическое пособие 638
.pdf
|
4 sin t cost |
cos2 t |
sin 2 t sin 2 t cos2 t |
|
0 . |
|
|
8sin 3 t cos3 t |
|||
|
|
|
|||
|
3.16. Дифференциалы высших порядков |
|
|||
Пусть функция y |
f x |
дифференцируема, а аргумент x яв- |
|||
ляется независимой переменной, то ее дифференциал или первый дифференциал dy y dx также является функцией x . Если дифференциал оказался дифференцируемой функцией x , то дифференциал от дифференциала функции y f x существует и называется
существует и называется
вторым дифференциалом или дифференциалом второго порядка :
d dy d 2 y d y dx |
y dx dx |
y dx dx |
y dx 2 y dx2 . |
Дифференциал n -го порядка определяется как дифференциал |
|||
от дифференциала n 1 -го порядка: |
|
||
|
d n y |
d d n 1 y . |
|
Данные формулы справедливы, если x |
является независимой |
||
переменной. В том случае, когда переменная |
x является функцией |
||
другой переменной, для дифференциалов второго и более высоких порядков справедливы другие формулы. Воспользуемся формулой d u  v v
v v  du u
du u  dv и получим:
dv и получим:
d 2 y d y dx d y
d y
 dx y
dx y d dx
d dx y
y dx2 y
dx2 y d 2 x .
d 2 x .
Можно заметить, что слагаемое y d 2 x появляется только в
d 2 x появляется только в
случае наличия сложной функции, когда x является функцией другой переменной. Если же x - независимая переменная, то
d 2 x d dx d 1
d 1 dx
dx dx
dx  d 1
d 1 0 .
0 .
59
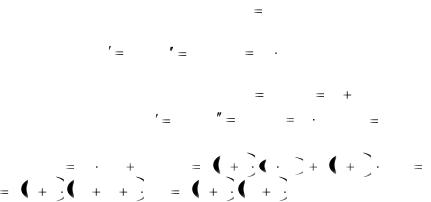
Пример.3.11. Найти d 2 y , |
если |
y |
x3 , а x |
является незвиси- |
||||
мой переменной величиной. |
|
|
|
|
|
|||
Решение. |
y |
3x2 , y |
6x , d 2 y 6x dx2 . |
|
|
|||
Пример.3.12. Найти |
d 2 y , если y |
x3 , а x |
t 2 |
1 . |
||||
Решение. Так как y |
3x2 , |
y |
6x , |
dx 2t |
dt , |
d 2 x 2d 2t , |
||
то |
|
|
|
|
|
|
|
|
d 2 y 6x dx2 |
3x2 2d 2t 6 t 2 |
1 2t dt 2 |
3 t 2 |
1 2 2d 2t |
||||
6 t 2 1 4t 2 |
t 2 |
1 d 2t |
6 t 2 |
1 5t 2 |
1 d 2t . |
|
|
|
Вопросы для самопроверки
1.Дайте определение дифференцируемой функции.
2.Что называется производной? Каков геометрический и физический смысл производной?
3.Всегда ли непрерывная функция имеет производную?
4.Сформулируйте основные правила дифференцирования.
5.Выведите формулу производной показательной функции исходя из определения производной.
6.Сформулируйте теорему о дифференцируемости обратной функции. Выведите формулы производных обратных тригонометрических функций, используя теорему о дифференцируемости обратных функций.
7.Что собой представляет логарифмическое дифференцирование? Когда целесообразно его использование?
8.Как производится дифференцирование сложных функций?
9.Выведите уравнения касательной и нормали к графику функции.
10.Как находится производная второго порядка параметрически заданной функции?
11.Дайте определение дифференциала функции.
60
Задачи для самостоятельного решения
Найти производные функций: |
|
|
|
|
|
|
||||||||||||||||
1. у= ln 2 (x3 |
|
sin x) . |
|
|
|
|
|
|
|
|
|
|
||||||||||
Ответ: y |
2 ln( x3 |
|
|
sin x) |
3x 2 |
cos x |
. |
|
|
|||||||||||||
(x3 |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
sin x) |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. y |
5sin 2 ( x2 |
1). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Ответ: y |
10x sin( x2 1) cos( x2 1) |
. |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
x2 |
1 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
3. y |
sin |
x |
sin 2x. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: y |
|
2sin |
x |
cos 2x |
|
1 |
cos |
x |
sin 2x . |
|||||||||||||
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
||
4. y arcsin 
 sin x.
sin x.
Ответ: y |
|
cos x |
|
. |
|
|
|
|
|||
|
|
|
|||
sin x sin 2 x |
|||||
2 |
|
|
|||
5. y xln x . |
|
|
|
||
Ответ. y
 2xln x 1 ln x.
2xln x 1 ln x.
6. y  ln x x .
ln x x .
Ответ: y |
ln x x |
1 |
ln ln x . |
|
|
||||
ln x |
||||
|
|
|
Найти производные функций, заданных параметрически:
7. x 1 t 2 , y t t 3.
61

Ответ: y |
3t 2 |
1 |
. |
2t |
|
||
|
|
|
|
8. x ln(1 t 2 ), |
y t arctgt. |
||
Ответ: y 2t .
2t .
Найти производные неявно заданных функций:
9. y2 |
2xy |
a2 |
0 . |
|
|
|
||||||
Ответ: |
|
dy |
|
|
|
y |
. |
|
|
|
||
|
|
|
|
|
|
|
|
|
||||
|
|
dx |
|
y |
x |
|
|
|
||||
10. y |
cos 2x |
y . |
|
|
|
|||||||
Ответ: |
|
dy |
- |
|
|
sin 2x |
y |
. |
||||
|
|
|
|
|
|
|
|
|||||
|
|
dx |
1 |
sin 2x |
|
y |
||||||
11. cos xy |
x . |
|
|
|
|
|
||||||
Ответ: |
|
dy |
|
- |
1 |
y sin xy |
. |
|||||
|
|
dx |
|
|
|
|
x sin xy |
|
|
|
||
Найти тангенс угла наклона касательной к кривой
12. x = t - sin t, y = 1 - cost при t |
|
. |
2 |
Ответ: tg 1 .
1 .
Вычислить производные различных порядков:
13. y |
c2 |
|
x2 . Найти y 2 . |
|||||
Ответ: |
y |
(2) |
= |
|
c2 |
|
. |
|
|
3 |
|
||||||
|
|
|
|
|
|
|||
|
|
|
|
|
c2 x2 |
|
|
|
|
|
|
|
2 |
|
|
||
62

14. y x2 a2 arctg |
x |
.Найти |
y 3 . |
|
a |
||||
|
|
|
|
|
|
Ответ: |
|
y 3 |
|
|
|
|
|
4a3 |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
a2 |
|
x2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
15. |
y |
sin |
2 |
x . Найти y |
(n ) |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
2(x |
n |
) |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
Ответ: |
|
y |
(n ) |
= - 2 |
n |
2 |
|
. |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16. |
y3 |
|
x3 |
3xy |
|
|
0 . Найти |
d 2 y |
. |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
dx2 |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Ответ: |
|
y 2 |
|
|
|
|
|
2xy |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
y 2 |
|
x 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
17. |
x |
a cost , y |
|
|
a sin t . Найти |
|
d 3 y |
. |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
dx3 |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Ответ: |
|
d 3 y |
=- |
|
|
3cos t |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
dx3 |
|
a |
2 sin 5 t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
18. Написать уравнение касательной и |
нормали |
к кривой |
||||||||||||||||||||||||||||||
|
x2 |
|
y 2 |
|
1 в точке M 1,1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
a2 |
|
b2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Ответ: уравнение касательной |
|
|
y = |
- |
b2 x |
1 |
b2 |
, |
уравнение |
|||||||||||||||||||||||
|
|
|
|
|
a2 |
a2 |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
нормали y |
a2 x |
1- |
|
a2 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
b2 |
|
|
|
b2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
63

4. ТЕОРЕМЫ О ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЯХ
|
|
|
|
|
|
|
|
|
4.1. Теорема Ролля |
|
|
|
|
|
|
|
|
|||||||||
|
Ряд теорем о дифференцируемых функциях имеет большое |
|||||||||||||||||||||||||
теоретическое и прикладное значение. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
Теорема Ролля. Если функция y |
|
f |
x |
непрерывна на отрезке |
|||||||||||||||||||||
a,b , |
дифференцируема на интервале |
a,b |
и на концах отрезка |
|||||||||||||||||||||||
принимает одинаковые значения |
|
f |
a |
|
f b , то найдется хотя бы |
|||||||||||||||||||||
одна точка |
c |
a,b , |
в которой производная |
f |
|
x |
обращается в |
|||||||||||||||||||
нуль, т.е. f |
c |
0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Доказательство. Так как функция y |
f |
x |
|
непрерывна на от- |
||||||||||||||||||||
резке |
a, b , |
то она достигает на этом отрезке своего |
наибольшего и |
|||||||||||||||||||||||
наименьшего значения, соответственно, |
M и |
m . |
В тривиальном |
|||||||||||||||||||||||
случае M |
m функция |
y |
|
f x |
постоянна на |
|
a,b |
и, |
следова- |
|||||||||||||||||
тельно, еѐ производная |
f |
x |
|
0 в любой точке отрезка |
a,b . |
|||||||||||||||||||||
|
|
В случае M |
m функция достигает хотя бы одно из значений |
|||||||||||||||||||||||
M |
или |
m |
во |
внутренней |
|
точке |
c |
интервала |
a,b , так как |
|||||||||||||||||
f a |
|
f |
b . |
Предположим, что функция принимает значение M в |
||||||||||||||||||||||
точке c , т.е. f c |
M . Тогда для |
любого x |
a,b |
будет выпол- |
||||||||||||||||||||||
няться неравенство |
f c |
|
f |
x |
. Найдем производную |
f |
x |
в точке |
||||||||||||||||||
x |
c : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (c) |
|
lim |
|
f (c |
|
x) |
f (c) |
. |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Поскольку |
|
|
f |
c |
|
f |
x , |
|
то |
|
|
верно |
|
|
неравенство |
|||||||||
f c |
|
x |
f |
c |
0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Если |
x |
0, |
|
что соответствует стремлению аргумента x к |
||||||||||||||||||||
точке c справа, то |
|
f (c |
|
x) |
|
f (c) |
0 |
и поэтому |
|
f |
c |
|
0 . |
|
||||||||||||
|
|
|
|
x |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если |
x |
0, то |
f (c |
x) |
|
f (c) |
|
0 |
и |
f |
c |
|
|
0 . |
|
|
|
|||||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
64 |
|
|
|
|
|
|
|
|
|
|
|

Одновременно два неравенства f  c
c 0 и f
0 и f  c
c 0 могут выполняться в одном случае f c 0 . Таким образом,
0 могут выполняться в одном случае f c 0 . Таким образом,
f c 0 .
Случай, когда f c m , может быть доказан по аналогии. Геометрический смысл теоремы Ролля сводится к тому, что на
m , может быть доказан по аналогии. Геометрический смысл теоремы Ролля сводится к тому, что на
графике дифференцируемой функции y  f x найдется точка, в которой касательная к графику параллельна оси Ox .
f x найдется точка, в которой касательная к графику параллельна оси Ox .
y
f  c 0
c 0
f a f b
f b
0 |
a c |
b x |
Рис. 14.
Важным следствием теоремы Ролля является то, что между двумя нулями дифференцируемой функции обязательно найдется хотя бы одна точка, где производная этой функции обращается в нуль.
4.2. Теорема Лагранжа |
|
|
Теорема Лагранжа. |
Если функция y f |
x непрерывна на |
отрезке a,b , дифференцируема на интервале |
a,b , то найдется |
|
хотя бы одна точка c a,b , такая, что выполняется равенство |
||
f (b) |
f (a) f ' (c)(b a). |
|
Доказательство. Рассмотрим вспомогательную функцию
65

F (x) |
f (x) |
f (a) |
|
f (b) |
f (a) |
(x a). |
|
|
|
|
|||||
|
|
|
|
b |
a |
|
|
Вспомогательная функция удовлетворяет всем условиям тео- |
|||||||
ремы Ролля, поскольку непрерывна на отрезке a,b |
и дифференци- |
||||||
руема на интервале |
a,b |
, на концах отрезка принимает одинако- |
|||||
вые значения F a |
F b |
0 . |
По теореме Ролля |
найдется такая |
|||
внутренняя точка c |
a,b , |
что |
F c |
0 , т.е. |
|
||||||
F |
c |
0 |
f |
c |
|
f |
b |
f a |
или |
||
|
|
|
|
|
|||||||
|
|
b |
a |
||||||||
|
|
|
|
|
|
|
|
|
|||
|
|
f |
c |
|
|
f b |
f |
a |
. |
|
|
|
|
|
|
b |
a |
|
|
||||
|
|
|
|
|
|
|
|
|
|||
Полученную формулу называют формулой Лагранжа, а теорему – теоремой о конечном приращении: приращение дифференцируемой функции на отрезке a,b равно приращению аргумента,
умноженному на значение производной функции в некоторой внутренней точке этого отрезка.
|
Теорема Лагранжа имеет простой геометрический смысл. Отно- |
||||||||||
шение |
|
f (b) |
f (a) |
есть тангенс угла наклона секущей |
AB , а вели- |
||||||
|
b |
a |
|||||||||
|
|
|
|
|
|
|
|
|
|
||
чина |
f |
c равна |
угловому коэффициенту касательной к |
кривой |
|||||||
y |
f |
x |
в точке с абсциссой |
x c . |
Таким образом, |
на графике |
|||||
|
|
|
|
|
|
|
|
функции |
y |
f |
x най- |
|
|
y |
|
|
|
B |
дется |
такая |
точка |
||
|
|
|
|
|
|
|
M c, f c |
, |
в |
которой |
|
f |
b |
|
|
|
|
|
|
||||
|
|
|
|
|
|
касательная |
к графику |
||||
|
|
|
|
|
|
|
|
||||
f |
c |
|
|
|
M |
|
функции |
параллельна |
|||
|
|
|
|
|
|
секущей AB . |
|
||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
A |
|
|
|
|
|
|
|
f |
a |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
a |
|
c |
b |
x |
|
|
|
|
|
|
|
|
|
Рис. 15. |
|
|
|
|
|
66

|
|
|
4.3 Теорема Коши |
|
|
|
|
|||
Теорема Коши. Если функции |
y f |
x |
и y |
x |
непре- |
|||||
рывны на отрезке |
a, b , дифференцируемы на интервале |
a,b , |
||||||||
причем |
x 0 |
для x a,b , то найдется хотя бы одна точка |
||||||||
c a,b |
такая, что выполняется равенство |
|
|
|
|
|||||
|
|
|
f (b) f (a) |
f (c) |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(b) (a) |
(c) |
|
|
|
|
||
Доказательство. Предполагается, |
что |
b |
a |
0 , так как в |
||||||
противном случае по теореме Ролля нашлась бы такая точка |
c , что |
|||||||||
 c 0 , что противоречит условию теоремы. Рассмотрим вспомогательную функцию
c 0 , что противоречит условию теоремы. Рассмотрим вспомогательную функцию
F (x) f (x) f (a) |
f (b) |
f (a) |
( (x) |
(a)). |
|
|
|||
|
(b) |
(a) |
|
|
Вспомогательная функция удовлетворяет всем условиям тео- |
||||
ремы Ролля, поскольку непрерывна на отрезке a,b |
и дифференци- |
|||
руема на интервале a,b , на концах отрезка принимает одинаковые
значения F a |
F b |
|
0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
По теореме Ролля существует такая точка c a,b , что |
|
|||||||||||||||||
F c 0 . Так как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
x |
f |
x |
|
f (b) |
f (a) |
(x), |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
(b) |
(a) |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F'(c) |
f '(c) |
f (b) |
f (a) |
'(c) 0 |
, f '(c) |
|
f (b) |
f (a) |
'(c) . |
|||||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
(b) |
(a) |
|
(b) |
(a) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Из последнего следует, что |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
f (b) |
|
|
f (a) |
f ' (c) |
. |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
(b) |
|
|
(a) |
' (c) |
|
|
|
|
|
|||||
67

|
|
|
4.4. Правило Лопиталя |
|
||||||||||||||
Теорема Лопиталя. Пусть функции |
|
f |
x |
и x |
непрерывны |
|||||||||||||
и дифференцируемы в окрестности точки |
x0 |
и обращаются в нуль в |
||||||||||||||||
этой точке, т.е. f x0 |
|
x0 |
0 , кроме того |
|
|
x0 |
0 , тогда, если |
|||||||||||
существует предел |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
f ' (x) |
|
A , то |
lim |
f (x) |
|
|
A . |
|
||||||||
|
' (x) |
|
|
|
|
|
|
|
||||||||||
x x0 |
|
|
|
x x0 |
(x) |
|
|
|
|
|||||||||
Доказательство. По теореме Коши для функций |
f x и x , |
|||||||||||||||||
непрерывных и дифференцируемых |
на отрезке |
x0 , x , найдется та- |
||||||||||||||||
кая внутренняя точка c |
|
x0 , x , что будет выполняться равенство |
||||||||||||||||
|
|
|
f (x) |
f (x0 ) |
|
|
f ' (c) |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
||
|
|
|
(x) (x0 ) |
' (c) |
|
|
|
|
||||||||||
Воспользовавшись тем, что f |
x0 |
|
x0 |
0 , получаем |
||||||||||||||
|
|
|
|
|
f (x) |
|
f (c) |
. |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
(x) |
|
|
(c) |
|
|
|
|
|
|
||||
Учитывая, что при x |
x0 величина с также стремиться к x0 , |
|||||||||||||||||
получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
f (x) |
|
lim |
|
f (c) |
. |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
x x0 |
(x) |
c x0 |
|
(c) |
|
|
|||||||||
Таким образом, предел отношения двух бесконечно малых равен пределу отношения их производных, если последний существует.
Если производные |
f x |
и |
x удовлетворяют тем же усло- |
||||
виям, что и функции f x |
и |
x , теорему можно применить еще |
|||||
раз: |
|
|
|
|
|
|
|
lim |
|
f (x) |
lim |
f (x) |
lim |
f (x) |
|
|
|
|
|
|
|||
|
(x) |
(x) |
(x) |
||||
x x0 |
x x0 |
x x0 |
|||||
68
