
Методическое пособие 638
.pdf
lim |
sin x |
= |
lim |
sin x |
=1. |
|
x |
x |
|||||
x 0 0 |
|
x 0 0 |
|
В этом случае функция доопределяется таким образом, чтобы устранить точку разрыва, т.е.
|
sin x |
, если x |
1, |
|
y |
x |
|||
|
|
|||
|
|
|
||
|
1, если x |
1. |
||
Если в точке |
a существуют |
конечные |
неравные пределы |
||
функции слева и справа (односторонние пределы), т. е. |
|||||
lim |
f x |
A, |
lim |
f x B , |
A B , |
x a |
0 |
x |
a |
0 |
|
то точка a называется точкой разрыва первого рода или скачком.
y
B
A
a |
x |
Рис. 5.
Точки разрыва первого рода или скачки часто имеют кусочнонепрерывные функции. Например, функция
|
|
f |
x = |
x |
1, |
если - 1 x 2 |
|
|
|
|
|
|
|
2 |
x, |
если |
2 x 5 |
|
|
испытывает |
скачек |
в |
точке |
x 2 , |
поскольку |
lim |
f x 1, |
||
|
|
|
|
|
|
|
x |
2 |
0 |
lim |
f x |
0 . |
|
|
|
|
|
|
|
x 2 |
0 |
|
|
|
|
|
|
|
|
Если хотя бы один из односторонних пределов стремится к бесконечности или не существует, то имеет место точка разрыва второго рода .
29

|
Например, |
функция |
y |
31/ x a |
разрывна, поскольку |
при |
|||||||||||
x |
a функция |
не |
определена |
(рис. |
6), |
а |
|
lim |
31/ x a |
, |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x a |
0 |
|
||
lim 31 / x a 0 . Точка x |
a является точкой разрыва второго рода. |
||||||||||||||||
x |
a 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для функции y |
|
1 |
(рис. 7) точка |
x |
0 является точкой раз- |
|||||||||||
|
|
|
|||||||||||||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
рыва второго рода, поскольку |
lim |
1 |
|
, |
lim |
1 |
|
. |
|
||||||||
|
|
|
|
|
|
|
|||||||||||
0 x |
0 x |
|
|||||||||||||||
|
|
|
|
|
|
x |
0 |
|
x 0 |
|
|
||||||
y |
|
|
|
y |
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
y 3 x a |
|
y |
|
||
|
|
|
|
|
|||
|
|
|
x |
||||
|
|
|
|
|
|
||
0 |
a |
|
x |
0 |
|
|
x |
|
|
|
|
|
|
|
|
Рис. 6. |
|
|
|
Рис. 7. |
|
|
|
Еще одним примером точки разрыва второго рода является |
|||||||
точка x 0 для функции y |
sin |
1 |
. В данном случае не существуют |
||||
x |
|||||||
|
|
|
|
|
|
||
правосторонний lim sin |
1 |
и левосторонний lim sin |
1 |
пределы |
|||
x |
x |
||||||
x 0 0 |
|
|
x 0 0 |
|
|||
|
|
|
|
|
|||
функции.
30

2.10. Основные теоремы о непрерывных функциях
Теоремы о непрерывности функций в точке a и ее окрестности следуют непосредственно из соответствующих теорем о пределах.
Теорема 1. Сумма двух функций, непрерывных в точке a и ее окрестности есть функция, непрерывная в точке a и ее окрестности.
|
Доказательство. |
Пусть функции |
u x и v x |
непрерывны в |
|||||||||||||
точке |
a |
и |
ее |
окрестности. Докажем непрерывность функции |
|||||||||||||
y |
u x |
v x , т.е. справедливость равенства |
lim |
|
y |
0 . |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
0 |
|
|
|
|
lim |
y |
lim |
|
u a |
x |
v a |
|
x |
u a |
v a |
|
|
|||
|
|
x 0 |
|
x |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
u a |
|
x |
|
u a |
|
lim |
v a |
x |
v a |
|
|
|
||
|
|
x |
0 |
|
|
|
|
|
|
x 0 |
|
|
|
|
|
|
|
|
|
lim |
u |
lim |
v . |
|
|
|
|
|
|
|
|
|
|||
|
|
x |
0 |
|
x |
0 |
|
|
|
|
|
|
|
|
|
||
|
Поскольку функции u x |
и v x |
непрерывны в точке a и ее |
||||||||||||||
окрестности, т.е. |
lim |
|
u 0 , lim |
v |
0 , то и |
lim |
y |
0 . |
|||||||||
|
|
|
|
|
x |
0 |
|
|
x 0 |
|
|
|
x |
0 |
|
|
|
|
Теорема 2. Произведение двух функций, непрерывных в точке |
||||||||||||||||
a и ее окрестности, |
есть функция, |
непрерывная в точке a и ее ок- |
|||||||||||||||
рестности. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Доказательство. Для доказательства непрерывности функции |
||||||||||||||||
y |
u x v x |
по аналогии с предыдущим доказательством покажем, |
|||||||||||||||
что |
lim |
y |
0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
y |
lim |
|
u a |
x v a |
x |
u a v a |
|
|
|
|||||
|
|
x 0 |
|
x |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
lim |
u a |
|
x v a |
x |
u a v a |
x |
u a v a |
x |
u a v a |
||||||||
x |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
u a |
x v a |
x |
|
u a v a |
x |
lim u a v a |
x |
u a v a |
|
|||||||
x |
0 |
|
|
|
|
|
|
|
|
x |
0 |
|
|
|
|
|
|
lim |
v a |
x |
u a |
x |
|
u a |
lim |
u a |
v a |
x |
v a |
|
|
|
|||
x |
0 |
|
|
|
|
|
|
|
x |
0 |
|
|
|
|
|
|
|
31

lim |
v a |
x |
u |
lim |
u a |
v v a lim |
u u a |
lim |
v |
0, |
|
x |
0 |
|
|
x |
0 |
|
x |
0 |
x |
0 |
|
где |
lim |
u |
0 , |
lim |
|
v |
0 , а функции u x |
и v x |
являются огра- |
||
|
x 0 |
|
|
x |
0 |
|
|
|
|
|
|
ниченными при x |
|
a . |
|
|
|
|
|
||||
|
Теорема 3. Частное от деления двух функций, непрерывных в |
||||||||||
точке a и ее окрестности есть функция, непрерывная в точке a и ее окрестности, если знаменатель в точке a не равен нулю.
Доказательство теоремы аналогично предыдущему доказательству.
Теорема 4. (Теорема о непрерывности сложной функции)
Пусть y f |
x -сложная функция. Если функция |
x непре- |
|||
рывна в точке a , а функция y |
f |
непрерывна в точке |
a |
a , |
|
|
|
|
|
|
|
то сложная |
функция y f |
x , составленная из непрерывных |
|||
функций, непрерывна в точке a (без доказательства). |
|
|
|||
2.11. Свойства функций, непрерывных на отрезке
Теорема Вейерштрасса о наибольшем и наименьшем зна-
чении функции на отрезке. Если функция непрерывна на отрезке, то она достигает на этом отрезке своего наибольшего и наименьшего значения (без доказательства).
y |
|
|
|
|
M |
y |
f |
x |
|
|
|
|||
m |
|
|
|
|
0 a x1 |
x2 |
b |
x |
|
|
Рис. 8. |
|
|
|
Изображенная на рис. 8 функция |
y |
f x непрерывна на от- |
||
резке a;b , принимает наибольшее значение M в точке x1 , а наи-
32
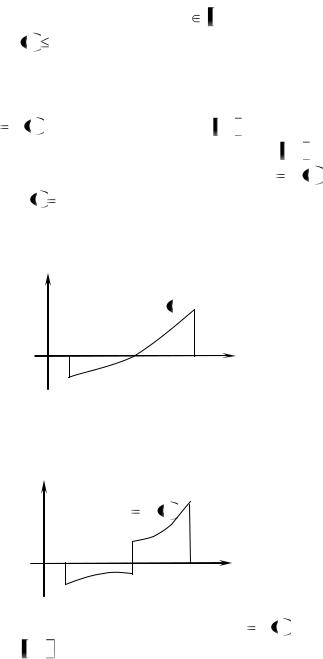
меньшее m - в точке x2 . Для любого x a;b имеет место нера-
имеет место нера-
венство m 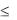 f x M .
f x M .
Следствие 1. Если функция непрерывна на отрезке, то она ограничена на этом отрезке.
Теорема о нуле непрерывной на отрезке функции. Если
функция y f x |
непрерывна на отрезке a;b , и на его концах |
|
принимает значения разных знаков, то внутри отрезка |
a;b найдет- |
|
ся хотя бы одна точка c , в которой данная функция y |
f x обра- |
|
щается в ноль: f c |
0 (без доказательства). |
|
Геометрический смысл теоремы заключается в том, что если график непрерывной функции переходит с одной стороны оси Ox на другую, то он обязательно пересекает ось Ox (рис.9).
y
y  f x
f x
a |
c |
b x |
Рис. 9.
В случае нарушения условия о непрерывности функции на отрезке вышеуказанная теорема может не выполняться(рис. 10).
y
y |
f x |
a |
c b x |
Рис. 10.
Теорема Больцано-Коши. Если функция y f x непрерыв-
на на отрезке a;b , и принимает на его концах неравные значения
33
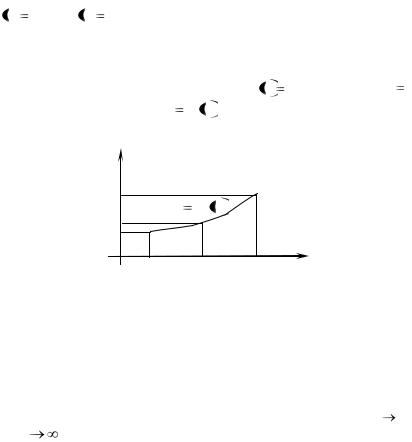
f a A и f b
A и f b B , то на этом отрезке она принимает и все про-
B , то на этом отрезке она принимает и все про-
межуточные значения между A и B (без доказательства). Геометрическая интерпретация теоремы Больцано-Коши сво-
дится к тому, что для любого числа C , заключенного между A и B ,
найдется такая внутренняя точка c , что f c |
C , т.е. прямая y C |
|||
пересечет график функции y |
|
f x |
, по крайней мере, в одной точке |
|
(рис. 11). |
|
|
|
|
y |
|
|
|
|
B |
y |
f |
x |
|
C |
|
|||
|
|
|
|
|
A |
|
|
|
|
a |
|
c |
b |
x |
Рис. 11.
|
Вопросы для самопроверки |
|
1. Сформулируйте определение предела функции при x a и |
при x |
. Дайте геометрическую иллюстрацию определений этих |
пределов.
2.Что такое бесконечно малая и бесконечно большая величины? Какова связь между бесконечно большой и бесконечно малой величиной?
3.Каковы основные свойства бесконечно малых величин?
4.Сформулируйте основные теоремы о пределах.
5.О чем говорится в первом замечательном пределе?
6.Как записываются основные формулы второго замечательного предела?
7.Какие бесконечно малые величины называются бесконечно малыми величинами одинакового порядка малости?
8.Приведите примеры эквивалентных бесконечно малых ве-
личин.
34

9.Дайте три определения непрерывности функции в точке.
10.Перечислите типы точек разрыва функции и опишите каждый из них.
11.Каковы основные теоремы о непрерывных в точке функци-
ях?
12.Сформулируйте свойства функций, непрерывных на отрез-
ке.
13.Какова геометрическая интерпретация теоремы о нуле непрерывной функции?
Задачи для самостоятельного решения
Вычислить пределы функций
|
1. |
lim |
|
|
x2 |
|
|
|
|
5 |
. |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
x |
|
2 x2 |
|
|
|
|
4 |
|
|
|
|||||||
|
2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
lim |
|
|
x3 |
|
3x 2 |
|
|
|
|
2x |
|
. |
|
||||||||||
2 x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
x |
|
|
|
x |
|
|
6 |
|
|
|
|
|
|
||||||||||
|
3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
lim |
|
4x3 |
|
|
2x2 |
1 |
. |
|
|
|
|||||||||||||
|
|
|
|
3x3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
x |
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|||||
|
4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
lim |
4x3 |
|
2x2 |
|
|
|
x |
. |
|
|
|
|
|||||||||||
|
|
|
|
3x2 |
|
|
|
2x |
|
|
|
|
|
|
|
|
|||||||
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
lim |
|
|
|
|
x2 |
|
|
x |
|
|
|
. |
|
|
|
|
|
|
|||||
|
x4 |
3x2 |
|
|
|
|
|
|
|
|
|
||||||||||||
x |
|
1 |
|
|
|
|
|
|
|
|
|||||||||||||
|
6. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
lim |
|
|
|
|
2x |
1 |
|
|
3 |
|
. |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
x |
2 |
|
|
|
|
2 |
|
|
|
|
|
|
||||||||
x 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
7. lim |
|
|
|
1 |
|
|
|
x |
2 1 |
. |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|||||||
|
|
|
|
|
|
x |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Ответ: 89 .
Ответ: 52 .
Ответ: 43 .
Ответ: 12 .
Ответ: 0.
Ответ: 2 32 .
Ответ: 0.
35

|
|
8. lim |
sin 2 (x / 3) |
. |
|
|
Ответ: |
|
1 |
. |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
9 |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
x |
0 |
|
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
9. lim |
|
tg2x |
. |
|
|
|
Ответ: |
|
2 |
. |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
x |
0 sin 5x |
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|||||||
|
10. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
x |
1 |
|
2 x |
1 |
|
|
|
|
|
Ответ: e6 . |
|
|
|
|
|
|||||||||||||||
lim |
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
11. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
2x |
|
3 |
|
|
x |
1 |
|
|
|
|
|
Ответ: е. |
|
|
|
|
|
|||||||||||||
lim |
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2x |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
12. Определить точки разрыва функции y |
|
|
|
|
|
x |
1 |
|
|
. |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
x(x |
1)(x2 |
4) |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Ответ: точки разрыва: x1 |
-2 , x2 |
|
|
1, |
|
x3 |
0 , |
x4 |
|
2 . |
|
|
|||||||||||||||||||
|
13. Найти точки разрыва функции |
y |
1 |
|
|
|
|
|
21/ x и построить |
|||||||||||||||||||||||
график этой функции. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Ответ: |
|
Разрыв |
второго |
рода |
|
при |
|
|
x |
0 |
( |
lim |
y |
, |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
0 |
0 |
|
lim |
|
y |
1). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x 0 |
-0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-2 sin 2x, |
если |
x |
|
|
|
; |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||||||||
|
14.Пусть |
f |
x |
Asin x B, |
если |
|
|
|
|
x |
|
; |
|
|
|
|
|
|||||||||||||||
|
2 |
|
|
2 |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
cos x, |
если |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Подобрать числа A и B так , |
чтобы функция |
f |
x |
была не- |
|||||||||||||||||||||||||||
прерывной ; построить еѐ график. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
Ответ: A |
1, |
B 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
36

3.ПРОИЗВОДНАЯ ФУНКЦИИ И ЕЕ ПРИЛОЖЕНИЯ
3.1. Дифференцируемость функции
Пусть имеется функция y f x , определенная и непрерывная в точке a и ее окрестности. Тогда некоторому приращению ар-
гумента |
x |
будет |
соответствовать |
приращение |
функции |
||||||||||
y f a |
x |
f |
a . |
|
|
|
|
|
|
|
|
|
|
|
|
Функция |
y |
f x |
называется дифференцируемой в точке a , |
||||||||||||
если приращение функции |
y |
имеет вид |
y |
A |
x |
|
|
x , где A |
|||||||
является |
только |
функцией |
a и |
не |
зависит |
от |
|
x , |
а |
x - |
|||||
бесконечно |
малая |
величина |
более |
высокого |
порядка |
малости по |
|||||||||
сравнению с приращением аргумента |
x , т.е. |
lim |
|
x |
0 . Глав- |
||||||||||
|
|
|
|
||||||||||||
|
x |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
x a |
|
|
|
|
|
ная линейная по |
x часть приращения функции называется диффе- |
||||||||||||||
ренциалом функции и обозначается символом dy |
или df |
a . Диф- |
|||||||||||||
ференциалом независимой переменной величины x является ее при-
ращение |
x , т.е. условно полагается , что dx |
x . |
|
|
|
|
|||||||
|
Рассмотрим предел отношения приращения функции |
y к |
|||||||||||
приращению |
аргумента |
|
x при x |
a для |
дифференцируемой |
||||||||
функции |
|
|
|
|
|
|
|
|
|
|
|
||
lim |
y |
lim |
A x |
x |
lim A |
x |
A |
lim |
x |
A . |
|||
|
|
|
|
|
|
|
|
||||||
x |
x |
|
x |
x |
|||||||||
x a |
x a |
|
x a |
|
x a |
|
|||||||
|
Величина A , определенная как предел отношения прираще- |
||||||||||||
ния функции к приращению аргумента при x |
a ( |
x |
0 ) играет |
||||||||||
очень важную роль, называется производной функции y |
f x |
по |
|||||||||||
независимой переменной x при данном ее значении x a и обозна-
чается y , f a , |
dy |
или |
df a |
. Тогда дифференциал dy записыва- |
|
dx |
dx |
||||
|
|
|
ется следующим образом: dy = y dx . Операцию нахождения произ-
водной называют дифференцированием.
Легко выяснить геометрический смысл производной и дифференциала функции. Введем сначала общее определение касательной
37
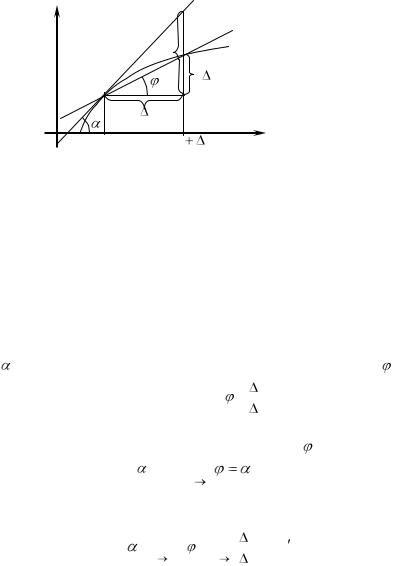
к кривой. Возьмем на непрерывной кривой L две точки M и M1
(рис. 12).
y |
|
|
|
|
dy |
M1 |
|
|
|
L |
|
|
|
|
|
M |
|
y |
|
|
|
|
|
|
x |
|
|
x |
|
x x |
x |
|
Рис. 12. |
|
|
Прямую MM1 , проходящую через эти точки, называют секущей. Пусть точка M1 двигаясь вдоль кривой L , неограниченно при-
ближается к точке M . Тогда секущая, поворачиваясь около точки M , стремиться к некоторому предельному положению .
Касательной к данной кривой в данной точке М называется предельное положение секущей MM1 , проходящей через точку М,
когда вторая точка пересечения M1 |
неограниченно приближается |
||
по кривой к точке |
M . Касательная к графику функции образует |
||
угол |
с осью Ох. |
Секущая MM1 |
образует с осью Ox угол . |
Угловой коэффициент секущей |
kсек = tg |
= |
y |
. При приближении |
|
|
|||||
|
|
|
x |
|
|
точки M1 к точке M секущая, |
поворачиваясь около точки M , пе- |
||||
реходит в касательную. Угол наклона касательной |
стремится к |
||||
углу наклона касательной , т.е. lim |
|
. Поэтому угловой ко- |
|||
|
x a |
|
|
|
|
эффициент касательной равен производной от ординаты y по абсциссе x
kкас |
= tg = lim tg |
= lim |
y |
= y . |
|
x |
|||||
|
x a |
x a |
|
38
