
Методическое пособие 638
.pdf
|
|
1.5.Некоторые классы функций |
|
|
||||||
Функция y |
f x |
называется возрастающей (убывающей) в |
||||||||
некоторой области, |
если для любой пары чисел x1 |
и x2 , принадле- |
||||||||
жащих этой области, большему значению аргумента |
x2 |
x1 будет |
||||||||
соответствовать большее |
f |
x2 f x1 |
(меньшее |
f x2 |
f x1 ) |
|||||
значение |
функции. |
Если |
же |
неравенству |
x2 |
x1 |
|
соответствует |
||
f x2 f |
x1 ( f x2 |
f |
x1 |
), |
то функция |
y |
f x |
называется не- |
||
убывающей (невозрастающей). Функция, удовлетворяющая одному из вышеназванных определений, называется монотонной. Напри-
мер, |
функция |
y |
x2 |
2x 4 монотонно убывает на промежутке |
||
,1 и монотонно возрастает на промежутке 1, . |
|
|
||||
|
Функция |
y |
f x |
называется ограниченной сверху (снизу) в |
||
некоторой области, |
если существует такое число А, |
что f x |
A |
|||
( f x |
A ) для любого x из этой области. Функция |
называется |
ог- |
|||
раниченной, если она ограничена сверху и снизу. В противном случае функция называется неограниченной.
Функция |
y f x , определенная в симметричной относи- |
|||
тельно |
начала |
координат |
области, |
называется четной, если |
f x |
f x , |
и нечетной, |
если f x |
f x . График нечетной |
функции симметричен относительно начала координат, а нечетной функции – относительно оси Oy .
Функция y |
f |
x |
называется периодической, если существу- |
|
ет такое число T |
0 , |
что для всех x из области определения вы- |
||
полняется условие |
f |
x |
T |
f x . Число T называется периодом. |
Наименьший положительный период, если он существует, называется основным периодом. Свойство периодичности функции подразумевает наличие области определения функции, простирающейся от  до
до  .
.
9

Вопросы для самопроверки
1.Что такое множество? Приведите примеры множеств и подмножеств.
2.Дайте определение суммы, произведения, разности мно-
жеств.
3.Что называется функцией? Приведите примеры функции, областью определения которой является отрезок на числовой оси, полубесконечный интервал.
4.Что является областью определения числовой последовательности?
5.Какие функции называются элементарными? Приведите примеры.
6.Приведите примеры алгебраической рациональной функции
иалгебраической иррациональной функции.
7.Какая функция называется сложной? Приведите примеры сложной функции, содержащей две промежуточные функции.
8.Дайте определение монотонно возрастающей функции, ограниченной функции.
9.Может ли нечетная функция иметь область определения
D y : 0, ?
2.ПРЕДЕЛ. НЕПРЕРЫВНОСТЬ ФУНКЦИИ
2.1Предел функции
Число A называется пределом функции y f x при x ,
при x ,
стремящемся к а ( x a ), если для любого сколь угодно малого положительного ε > 0 найдется такое δ(ε) > 0, что для всех х, удовле-
творяющих |
неравенству |
|
x |
a |
|
имеет |
место |
неравенство |
|||
|
f x A |
|
. Если A есть предел функции |
y |
f x |
при x a , |
|||||
|
|
||||||||||
то пишут |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
lim |
f x |
A . |
|
|
|
||
|
|
|
|
x a |
|
|
|
|
|
|
|
|
Определение предела |
|
функции |
y f |
x |
графически иллюст- |
|||||
рируется следующим образом (рис. 1). |
|
|
|
||||||||
10

|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
А+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||||
|
|
|
|
|
|
А |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
А- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а- |
а |
|
|
а+ |
x |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 1. |
|
|
|
|
|||||
Для сколь угодно малой |
-окрестности около |
ординаты |
A |
||||||||||||||||||||
найдется такая |
|
|
окрестность точки |
a , что для всех точек |
x |
из |
|||||||||||||||||
окрестности точки a |
точки графика функции |
y |
f x |
будут |
|||||||||||||||||||
лежать |
внутри |
|
|
полосы |
шириной 2 , ограниченной |
прямыми |
|||||||||||||||||
y A |
ε, y |
A |
|
|
ε . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Число |
A называется пределом |
функции y |
f x |
при |
x , |
||||||||||||||||||
стремящемся к бесконечности, если для любого сколь угодно малого
положительного ε > 0 найдется такое N , что для всех x |
N будет |
||||
|
A |
|
|
||
выполняться неравенство |
f x |
|
, что записывается следую- |
||
щим образом |
|
|
|
|
|
|
lim f |
x |
A . |
|
|
x |
|
|
|
|
|
Определение предела функции |
y f x при x |
графиче- |
|||
ски иллюстрируется следующим образом |
|
||||
у
А A+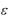
A-
О |
N |
х |
Рис. 2.
11

Для сколь угодно малой -окрестности около ординаты A найдется такое значение N , что для всех x N график функции не будет выходить за пределы полосы шириной 2 .
2.2.Бесконечно малые и их основные свойства
Функция y  (x) называется бесконечно малой величиной
(x) называется бесконечно малой величиной
при x a , если lim (x) 0 , т.е. для любого сколь угодно малого
xa
ε> 0 найдется такое δ(ε) > 0, что для всех x , удовлетворяющих не-
равенству |
x a |
, имеет место неравенство |
x |
. |
Любая константа, какой бы малой она ни была, не является бесконечно малой величиной.
|
Пример 2.1. Функция |
1 |
будет бесконечно малой при |
|||
|
|
|||||
|
x |
|||||
|
|
|
|
|
||
x |
, так как lim |
1 |
0 . Действительно, из определения предела |
|||
x |
||||||
|
x |
|
|
|
||
следует, что для любого наперед заданного произвольно малого положительного найдется такое число N, что для всех значений х,
удовлетворяющих неравенству |x| > N, |
1 |
|
0 |
|
. |
Имеем |
1 |
, |
||||||||||
|
|
|
|
|||||||||||||||
x |
|
x |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
| x | |
1 |
, тогда N |
1 |
, | x | |
N |
|
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Теорема 1. Если lim |
f |
x |
|
|
A, то ( f |
x |
A ) |
есть бесконечно |
|||||||||
|
|
|
|
x a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
малая величина, и наоборот: если |
f |
x |
A |
|
|
x , |
где x - беско- |
|||||||||||
нечно малая величина, то lim |
f |
x |
A. |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
x |
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Доказательство. Если |
|
lim |
f |
x |
A , |
то |
для любого |
мало- |
|||||||||
|
|
|
|
|
|
|
x a |
|
|
|
|
|
|
|
|
|
||
го |
0 можно указать такую |
|
|
|
окрестность около точки |
a , что |
||||||||||||
для |
всех x из |
этой окрестности |
будет |
выполняться условие |
||||||||||||||
12

|
f x |
A |
|
, а это и означает в соответствии с определением, что |
||||||
величина ( f |
x |
A) есть бесконечно малая величина. |
|
|||||||
|
|
Обратно, |
если f x A |
x |
при |
x |
a , то |
( f x A ) = |
||
|
x |
есть бесконечно малая, поэтому для любого |
0 найдется |
|||||||
такая |
|
окрестность около точки a , что для всех x |
из этой окре- |
|||||||
стности будет выполняться условие | |
| |
. Следовательно, для всех |
||||||||
значений у, начиная с некоторого, будет выполняться неравенство
|
f |
x |
|
|
A |
|
. А это и означает, что |
lim |
f x |
A . |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Теорема 2. Сумма конечного числа бесконечно малых вели- |
||||||||||||||||||||||
чин есть величина бесконечно малая. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
Доказательство. Пусть |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
x = |
1 x + 2 x + 3 x +…+ n x , |
|
|
|
||||||||||||
где |
|
i x есть бесконечно малые величины, |
|
i |
1,..n . |
|
Для каждой |
||||||||||||||||||||
бесконечно малое величины |
i x |
в соответствии с определением |
|||||||||||||||||||||||||
можно указать |
i - окрестность и |
i - окрестность. Тогда |
|||||||||||||||||||||||||
|
|
x |
|
|
|
|
|
1 x |
|
2 |
x |
... |
n x |
|
|
1 x |
|
|
2 x |
|
|
... |
|
n |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
1 |
|
|
2 ... |
n . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
Обозначим наибольшую из |
i - окрестностей как |
|
, тогда |
|||||||||||||||||||
|
|
x |
|
|
|
|
n . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
Обозначим наименьшую |
из |
i - окрестностей как |
|
. Можно |
||||||||||||||||||
утверждать, что для любого малого положительного |
|
|
найдется |
||||||||||||||||||||||||
такое |
, |
что |
для |
всех |
x , |
удовлетворяющих |
|
неравенству |
|||||||||||||||||||
|
x |
a |
|
, |
будет выполняться условие |
|
x |
|
|
|
. Последнее и оз- |
||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||
начает, что |
x есть бесконечно малая величина. |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
Теорема 3. Произведение любого числа бесконечно малых ве- |
||||||||||||||||||||||
личин есть бесконечно малая величина. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
Доказательство. Пусть |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x = 1 x |
|
2 x |
3 x … |
n x , |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 |
|
|
|
|
|
|
|
|
|
|
|

где i x есть бесконечно малые бесконечно малой величины i x можно указать i - окрестность и
величины, i 1,..n . Для каждой  в соответствии с определением i - окрестность. Тогда
в соответствии с определением i - окрестность. Тогда
|
x |
|
|
|
1 x |
2 |
x ... |
n x |
|
1 |
x |
|
2 |
x |
... |
|
n x |
|
|
|
1 |
|
2 ... |
n . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
Обозначим наибольшую из |
i - окрестностей как |
, тогда |
||||||||||||||
|
x |
|
|
|
n . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
Обозначим наименьшую из |
|
i - окрестностей как |
. Можно |
|||||||||||||
утверждать, |
что для любого малого положительного |
n найдется |
||||||||||||||||||
такое |
, |
что |
для |
всех |
x , |
|
удовлетворяющих |
неравенству |
||||||||||||
|
x a |
|
, |
будет выполняться условие |
|
|
x |
|
n . Последнее и |
|||||||||||
|
|
|
|
|
||||||||||||||||
означает, что x есть бесконечно малая величина. |
|||||||||||||
Теорема 4. Произведение бесконечно малой величины и огра- |
|||||||||||||
ниченной функции есть бесконечно малая величина. |
|||||||||||||
Доказательство. |
Для ограниченной функции y f x спра- |
||||||||||||
|
f x |
|
M , выполняемое для всех x из облас- |
||||||||||
ведливо неравенство |
|
|
|||||||||||
ти определения. Тогда для бесконечно малой |
x можно записать |
||||||||||||
|
|
|
f x |
|
x |
|
M |
|
x |
|
M . |
||
|
|
|
|
|
|
|
|||||||
Можно утверждать, что для любого сколь угодно малого M |
|||||||||||||
найдется такая - окрестность, что для всех |
x из этой окрестности |
||||||||||||
будет выполняться условие |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
f x |
|
x |
|
|
M , |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
что и соответствует определению бесконечно малой величины. Следствие 2. Произведение бесконечно малой величины на
константу есть бесконечно малая величина.
Функция |
y f x называется бесконечно большой величиной |
|
при x |
a , если для любого сколь угодно большого числа M най- |
|
дется такое |
0, зависящее от M , что для всех x из - окрест- |
|
14

ности будет выполняться условие f x M , что записывается следующим образом
M , что записывается следующим образом
|
|
|
lim f x |
. |
|
|
|
x a |
|
|
|
Теорема 4. Если x является бесконечно малой величиной, |
||
то |
1 |
|
есть бесконечно большая величина. |
|
|
|
|||
|
|
|||
|
x |
|
||
|
|
Доказательство. Поскольку величина |
x является бесконеч- |
|
но малой величиной, то для любого сколь угодно малого положи-
тельного |
|
0 найдется такая |
|
- окрестность около точки a , |
что |
||||||||||||||||||||||
для всех x из |
|
|
|
|
|
|
|
|
|
x |
|
|
|||||||||||||||
|
- окрестности будет выполняться условие |
|
|
|
. |
||||||||||||||||||||||
Поэтому |
для |
величины |
1 |
|
можно |
указать |
для любого |
числа |
|||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||
|
|
x |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
M |
1 |
0 такую |
|
|
- окрестность около точки a , что для всех x |
из |
|||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||
- окрестности будет выполняться условие |
|
|
M |
, что и озна- |
|||||||||||||||||||||||
|
1 |
|
|||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||
|
|
x |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
чает, что величина |
1 |
|
|
является бесконечно большой величиной. |
|||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||
|
x |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
2.3. Основные теоремы о пределах |
|
|
|
|
|
|
|||||||||||||||
|
Рассмотрим пределы функций при x |
|
|
a , |
полагая, |
что ре- |
|||||||||||||||||||||
зультаты не изменятся и при x |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
Теорема 1. Предел алгебраической суммы функций |
u x |
и |
||||||||||||||||||||||||
v x |
равен алгебраической сумме пределов этих функций. |
|
|
|
|
||||||||||||||||||||||
|
|
lim u x |
v x |
|
|
lim u x |
lim v x . |
|
|
|
|
|
|
|
|
|
|||||||||||
|
x |
a |
|
|
|
|
|
|
x |
a |
|
x |
a |
|
|
|
|
|
|
|
|
|
|
|
|||
|
Доказательство. |
Пусть |
|
lim u x |
u0 |
, lim v x |
v0 . |
Тогда |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
a |
|
|
x |
a |
|
|
|
|
|
|
|
|||
можно записать при x |
|
|
a , |
что u x = u0 + |
1 x , v x |
= v0 + |
2 |
x , |
|||||||||||||||||||
где |
1 x , 2 |
x |
- бесконечно |
малые |
величины. |
Следовательно, |
|||||||||||||||||||||
15

u x + v x = u0 + v0 + |
1 x + |
2 |
|
|
x . Здесь u0 + v0 |
– постоянная вели- |
|||||||||||||||||||||||||
чина, а |
|
1 x + |
2 |
x |
– бесконечно малая величина. Если функция |
||||||||||||||||||||||||||
u x + v x |
|
|
при |
x |
|
a |
представляется в |
виде |
суммы |
константы |
|||||||||||||||||||||
u0 + v0 |
и бесконечно малой величины, |
то по первой теореме о бес- |
|||||||||||||||||||||||||||||
конечно малых величинах предел этой функции равен u0 + v0 . |
|
|
|||||||||||||||||||||||||||||
|
Пример 2.2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
lim |
|
5x2 |
|
6x |
|
lim |
5 |
|
6 |
|
|
lim 5 |
lim |
|
6 |
|
5 . |
|
|
|
||||||||||
|
|
|
x2 |
|
|
|
x |
|
|
x |
|
|
|
||||||||||||||||||
|
x |
|
|
|
|
|
x |
|
|
x |
|
|
|
x |
|
|
|
|
|
|
|
|
|||||||||
|
Теорема 2. Предел произведения функций u x и |
v x равен |
|||||||||||||||||||||||||||||
произведению пределов этих функций. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
lim |
u x |
v x |
|
|
lim u x |
lim v x . |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
x |
a |
|
|
|
|
|
|
x |
|
a |
|
|
|
x |
a |
|
|
|
|
|
|
|
|
|
|
Доказательство. Пусть lim u x |
u0 , |
lim v x |
v0 . Тогда |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
a |
|
|
|
|
|
x |
a |
|
|
|
|
|
|||||
можно записать при x |
a , что u x = u0 + |
|
1 x , v x = v0 + 2 |
x , |
|
||||||||||||||||||||||||||
где |
1 x ; |
|
|
2 |
x - бесконечно малые величины. Имеем |
|
|
|
|||||||||||||||||||||||
|
|
|
lim |
u x |
v x |
lim |
|
|
u0 |
|
|
1 |
x |
|
v0 |
|
2 x |
|
|
|
|||||||||||
|
|
|
x |
a |
|
|
|
|
x |
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
lim u0v0 |
u0 |
2 x |
|
|
|
|
v0 |
1 |
x |
|
1 |
x |
2 |
x |
u0v0 . |
|
|
||||||||||
|
|
|
|
x |
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Следствие. Постоянный множитель можно выносить за знак |
||||||||||||||||||||||||||||||
предела: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
lim |
cv x |
|
|
c lim v x . |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
x |
a |
|
|
|
|
|
|
|
x |
a |
|
|
|
|
|
|
|
|
|
|
|
|
Теорема 3. Предел частного от деления двух функций u x |
и |
|||||||||||||||||||||||||||||
v x |
равен частному от деления пределов этих функций |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u x |
|
|
|
lim u x |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
x |
|
a |
|
|
. |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
v x |
|
|
|
|
lim v x |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
x |
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
a |
|
|
|
|
|
|
|
|
|
|
Доказательство. Пусть |
|
|
lim |
u x |
u0 |
, |
|
|
lim v x |
v0 . |
Тогда |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x a |
|
|
|
|
|
|
|
x |
a |
|
|
|
|
|||||
можно записать при |
x |
a , |
|
что |
u x = u0 + |
1 x , |
v x = v0 + |
2 |
x , |
||||||||||||||||||||||
где |
1 x ; |
|
|
2 |
x - бесконечно малые величины. |
|
|
|
|
|
|||||||||||||||||||||
|
Имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
16

lim |
u x |
|
|
lim |
|
u0 |
1 |
x |
lim |
u0 |
|
|
|
u0 |
1 |
x |
|
u0 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
x a |
v x |
|
|
x a v0 |
2 |
x |
x a |
v0 |
|
|
|
v0 |
2 |
x |
|
v0 |
|
|||||||||||||||
|
u0 |
|
lim |
|
u0v0 |
|
1 x v0 u0v0 |
u0 2 x |
|
|
|
u0 |
|
lim |
1 x v0 u0 2 x |
|
|
|||||||||||||||
|
v0 |
|
|
|
|
|
v0 v0 |
|
2 x |
|
|
|
|
v0 |
|
v0 v0 |
2 x |
|
||||||||||||||
|
x a |
|
|
|
|
|
|
|
|
|
|
|
x a |
|
||||||||||||||||||
|
|
u0 |
lim |
|
x |
|
1 |
|
|
lim |
|
|
x |
|
u0 |
|
|
|
|
u0 |
, |
|||||||||||
|
|
v0 |
1 |
v0 |
|
2 x |
2 |
v0 |
v0 |
2 x |
|
|
|
|
v0 |
|||||||||||||||||
|
|
x a |
|
|
|
|
|
x a |
|
|
|
|
|
|
|
|
|
|||||||||||||||
где два последних предела обращаются в нуль, поскольку являются пределами произведений бесконечно малых величин на ограниченные функции.
Теорема 4. Если lim |
f x |
A, а функция y принимает неотри- |
|
x |
a |
|
|
цательные значения y |
0 , |
то |
A есть неотрицательное число A 0 |
(без доказательства).
Теорема 5. Если между соответствующими значениями двух
функций u |
u(x) и v=v(x) |
выполняется неравенство u(x) |
v(x) и |
||||||||||||||||
lim u(x) |
u0 , lim v(x) |
|
v0 , то имеет место неравенство u0 v0 . |
|
|||||||||||||||
x a |
|
x |
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Доказательство. Поскольку u(x) |
v(x) |
0 , то по предыдущей |
|||||||||||||||||
теореме |
lim (u(x) |
v x) |
0 , |
или |
|
lim u x |
lim |
v x |
0 . |
Отсюда |
|||||||||
|
x |
a |
|
|
|
|
|
|
x |
a |
|
x |
a |
|
|
|
|
|
|
следует, что |
lim u(x) |
lim v x , т.е. u0 |
v0 . |
|
|
|
|
|
|
|
|
|
|||||||
|
|
x |
a |
|
x |
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
Теорема |
6. |
|
Если |
|
lim u(x) |
u0 , |
|
lim |
v(x) |
u0 |
и |
||||||||
|
|
|
|
|
|
|
|
x |
a |
|
|
|
|
x a |
|
|
|
|
|
u(x) z x |
|
v(x) , то |
lim z(x) |
u0 |
(без доказательства). |
|
|
||||||||||||
|
|
|
|
x |
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Теорема 7. Если функция |
y |
f |
x |
при |
x |
a |
является не- |
||||||||||||
|
|
|
|
|
f x |
|
M , |
|
|||||||||||
убывающей |
и |
ограничена сверху числом |
|
M , т.е. |
|
|
то |
||||||||||||
функция y |
f |
x имеет предел при x |
a (без доказательства). |
|
|||||||||||||||
17

Пример 2.3. Вычислить предел |
lim |
7x2 |
2x |
. |
|
|
|
|||||||
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
x 1 3x 4 |
1 |
|
|
|
|
|
|
7x |
2 |
2x |
|
lim 7x2 |
2x |
7 lim x2 |
2 lim x |
9 |
|
||||
lim |
|
|
x 1 |
|
|
x 1 |
x 1 |
. |
||||||
|
|
|
|
lim 3x4 |
|
|
3lim x4 |
|
|
|
|
|||
x 1 3x4 |
1 |
|
1 |
|
lim 1 |
2 |
|
|||||||
|
|
|
|
|
x 1 |
|
|
x 1 |
x 1 |
|
|
|
||
Если при вычислении пределов алгебраической суммы, произведения или частного от деления функций сами функции стремятся к некоторым константам, не равным одновременно нулю в случае деления функций, то вычисление пределов как в предыдущем примере не вызывает затруднения. Пределы отношения бесконечно малых величин, отношения бесконечно больших величин, произведения бесконечно малой и бесконечно большой величины в зависимости от частного закона изменения рассматриваемых величин могут принимать различные значения или даже не существовать. Выраже-
ния |
вида |
0 |
|
, |
|
|
|
, 0 |
, |
, 1 |
называются |
неопределенно- |
|
0 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
стями. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.4. Предел функции |
sin x |
при x |
0 |
||||||
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
(первый замечательный предел) |
|
||||||
|
Функция |
y |
sin x |
не определена при x 0 . Найдем предел |
|||||||||
|
x |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
этой |
функции |
|
при |
x |
0 . |
Рассмотрим окружность радиуса R . |
|||||||
Пусть острый центральный угол MOA равен x (рис. 11).
М С
R
x
О А
В
Рис. 3.
18
