
Методическое пособие 638
.pdf
гиперболический котангенс |
|
|
|
|
|
|
|
chx |
|
e x |
e |
x |
|
cthx |
|
|
|
|
|
. |
shx |
|
e x |
e |
x |
||
Между гиперболическими функциями существуют соотношения, аналогичные соотношениям между тригонометрическими функциями:
|
|
|
|
|
|
|
|
|
ch2 x |
|
sh 2 x |
1; |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
sh x |
|
|
y |
shx chy |
|
|
shy |
chx ; |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
ch x |
|
|
y |
chx chy |
|
|
shx |
shy ; |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
th x |
y |
|
|
|
thx |
|
|
thy |
|
; |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
1 thx thy |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
sh2x 2shx |
chx ; |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
ch2x ch2 x sh2 x . |
|
|
|
|
|
|
|
|
|
||||||||||||||
Найдем производные гиперболических функций: |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
shx |
|
|
e x |
e |
x |
|
|
e x |
|
e |
x |
chx |
; |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
chx |
|
e x |
e x |
|
|
|
|
e x |
|
e |
x |
shx ; |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
thx |
shx |
|
|
|
shx |
chx |
shx chx |
|
|
|
ch2 x |
sh2 x |
|
|
1 |
|
; |
|||||||||||||
chx |
|
|
|
|
|
ch2 x |
|
|
|
|
|
|
|
|
|
|
ch2 x |
|
ch2 x |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
cthx |
|
chx |
|
|
chx |
shx |
chx shx |
|
|
|
|
sh2 x |
ch2 x |
1 |
|
; |
||||||||||||||
|
shx |
|
|
|
|
|
sh2 x |
|
|
|
|
|
|
|
|
|
|
|
sh2 x |
|
|
sh2 x |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
49

3.7. Таблица производных
|
y x |
|
|
y |
x |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. |
|
c |
0 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. |
x |
|
|
x |
1 |
|||||||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. |
|
|
|
|
|
1 |
|
|
|
|
||||
|
|
x |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
x |
|||||
|
|
|
|
|
|
|
|
|
|
|
||||
4. |
1 |
|
|
1 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
x |
|
|
|
x2 |
||||||||
5. |
a x |
a x ln a |
||||||||||||
|
|
|
|
|
|
|
|
|||||||
6. |
e x |
|
|
e x |
||||||||||
|
|
|
|
|
|
|
|
|||||||
7. |
loga x |
|
1 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
x ln a |
|||||||
8. |
ln x |
1 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
9. |
sin x |
|
cos x |
|||||||||||
|
|
|
|
|
||||||||||
10. |
cos x |
|
|
sin x |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y x |
|
|
|
y |
x |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11. |
tgx |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos2 x |
||||||||||
12. |
ctgx |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
sin2 x |
||||||||
13. |
arcsin x |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
x 2 |
|||||||||
14. |
arccos x |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
x 2 |
|||||||||
15. |
arctgx |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
1 |
x2 |
|||||||||
16. |
arcctgx |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
1 |
x2 |
|||||||||
17. |
shx |
|
|
|
|
chx |
||||||||
|
|
|
|
|
|
|
|
|||||||
18. |
chx |
|
|
|
|
shx |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
19. |
thx |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
ch 2 x |
|||||||||
20. |
cthx |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
sh2 x |
|||||||||
50

3.8.Метод логарифмического дифференцирования
Внекоторых случаях перед нахождением производной можно прологарифмировать исходную функцию и только после этого дифференцировать. Данный метод называется логарифмическим дифференцированием. Метод логарифмического дифференцирования облегчает взятие производной функции, содержащей большое количество множителей.
|
Пример |
|
3.1. |
Найти |
производную |
функции |
|||
|
|
|
|
|
|
|
|
|
|
y |
sin 2 x |
3 |
4 |
x 5 |
|
. |
|
|
|
ctg |
3 x |
2 x 1 |
|
|
|
|
|||
|
|
|
|
|
|
||||
Решение. Обычный вариант нахождения производной с помощью правил дифференцирования оказывается достаточно громоздким, поэтому предварительно прологарифмируем функцию:
ln y 2 ln sin x |
5 |
ln 4 x 3ctgx x 1 ln 2 . |
|
3 |
|||
|
|
Продифференцируем данное равенство по x :
y |
|
2 cos x |
5 |
3 |
|
ln 2 . |
||
|
|
|
|
|
|
|
|
|
y |
|
sin x |
|
3 4 x |
|
sin 2 |
|
|
|
|
|
x |
|||||
Выражаем производную:
|
y |
|
y |
|
2cosx |
- |
|
5 |
|
|
|
3 |
|
- ln2 , |
|
|||||
|
|
|
sinx |
|
3 4 - x |
|
|
|
sin 2 x |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
y |
sin 2 |
x |
3 |
|
4 x 5 |
|
|
|
2cosx |
|
- |
5 |
|
|
3 |
- ln2 . |
||||
ctg |
3 x |
2 x 1 |
|
|
sinx |
3 4 - x |
|
sin 2 x |
||||||||||||
|
|
|
|
|
|
|
||||||||||||||
Метод логарифмического дифференцирования оказывается единственным способом нахождения производной для показатель-
но-степенной функции y |
u x v x : |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
u |
|
ln y v lnu , |
y |
|
v ln u v |
|
u |
, y |
y v ln u v |
, |
||
y |
|
u |
u |
|||||||
|
|
|
|
|
|
|
||||
|
|
|
|
|
51 |
|
|
|
|
|

y u v v
u v v ln u v uu .
ln u v uu .
Пример 3.2. Найти производную функции y  x4 1 sin x .
x4 1 sin x .
Решение. Воспользовавшись предыдущей формулой, получа-
ем:
y |
x4 |
1 |
sin x |
x4 1 |
sin x |
cos x ln x4 1 sin x |
4x3 |
|
. |
|
|
x4 |
1 |
||||||
|
|
|
|
|
|
|
|
3.9. Производная параметрически заданной функции
Пусть зависимость между аргументом x и функцией y задана параметрическим образом посредством двух уравнений
yy t , x x t ,
где t - вспомогательная переменная величина, называемая параметром. Параметр принимает непрерывный ряд значений из некоторого
промежутка t1 t |
t2 . |
|
|
|
|
|
|
|||
|
Предполагается, |
что функции y |
|
y t и x x t имеют про- |
||||||
изводные, причем последняя функция |
|
имеет обратную |
функцию |
|||||||
t |
(x) , тогда y |
y |
(x) является сложной функцией. По правилу |
|||||||
дифференцирования сложной функции имеем: |
|
|||||||||
|
|
|
|
|
|
y'x y't |
|
'(x) . |
|
|
|
Воспользовавшись теоремой о производной обратной функ- |
|||||||||
ции, заменим |
|
на |
1 |
|
. В результате подстановки имеем |
|
||||
x |
xt |
|
|
|||||||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y x |
yt |
. |
|
|
|
|
|
|
|
|
xt |
|
|||
|
|
|
|
|
|
|
|
|
||
|
Данная формула позволяет вычислять производную |
y x от па- |
||||||||
раметрически заданной функции, не находя непосредственной зависимости y от x .
52

Пример 3.3. Найти производную |
y x |
параметрически задан- |
||||||||||||||||||||||||||
ной функции |
|
x |
a cost, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
y |
b sin t. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Решение. |
Вычислим производные |
|
y't |
bcost, |
x't |
a sin t . |
||||||||||||||||||||||
Тогда y'x |
|
|
b cost |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
a sin t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 3.4. Найти производную y x параметрически заданой |
||||||||||||||||||||||||||||
функции |
x |
|
|
a(t |
|
sin t), . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
y |
|
|
a(1 cost). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Решение. |
|
|
Вычислим |
|
соответствующие |
производные |
||||||||||||||||||||||
yt a sin t , |
x |
a 1 |
cost |
. Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 sin |
|
t |
cos |
|
t |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
sin t |
|
|
|
|
|
|
|
|
|
t |
|
|
|
||||||
|
|
|
|
|
y'x |
|
|
2 |
2 |
|
|
ctg |
. |
|
|
|||||||||||||
|
|
|
|
|
1 |
cos t |
|
2 sin |
2 t |
|
|
|
|
2 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
3.10. Неявная функция, и ее дифференцирование |
|||||||||||||||||||||||||||
Неявно заданной функцией называется функция, задаваемая |
||||||||||||||||||||||||||||
уравнением |
|
F x, y |
|
|
0 , |
не разрешенным относительно y . Любую |
||||||||||||||||||||||
явно заданную функцию |
y |
f x |
можно записать как неявно за- |
|||||||||||||||||||||||||
данную |
уравнением |
|
f |
x |
y |
0 . |
Переход |
от неявного |
задания |
|||||||||||||||||||
функции к явному заданию часто невозможен ввиду сложности свя-
зи переменных |
x |
и y , |
как, например, в неявно заданной функции |
||
y sin |
xy |
2x |
y |
0 . |
|
Для |
того, |
чтобы |
найти производную неявной функции |
||
F x, y |
0 , не преобразовывая ее в явную, продифференцируем обе |
||||
части уравнения по x , считая, что y есть функция от x . Полученное уравнение разрешается относительно y .
.
53

Пример 3.5. Найти производную функции, заданной неявным образом: x y e xy .
e xy .
Решение. Дифференцируем левую и правую части уравнения
по x : |
|
|
|
|
|
|
1 y |
exy y xy |
или y 1 |
xexy |
yexy 1. |
||
Разрешая уравнение относительно y , находим производную |
||||||
|
|
y |
yexy |
1 |
. |
|
|
|
1 xexy |
|
|||
|
|
|
|
|
||
3.11. Уравнение касательной и нормали к графику функции |
||||||
Рассмотрим |
график |
функции |
y f |
x . Выберем точку |
||
M x0 , f x0 , принадлежащую кривой, |
и проведем через эту точку |
|||||
касательную. Касательная как наклонная прямая линия, проходящая через точку M , имеет уравнение вида
y |
f x0 k x |
x0 . |
|
|
Угловой коэффициент |
касательной |
k |
равен |
производной |
функции, посчитанной в точке касания x0 , т.е. |
k f |
x0 . В резуль- |
||
тате получаем уравнение касательной к графику функции в точке x0
(рис. 13)
|
y f x0 |
f x0 x x0 . |
|
|||
y |
|
|
y f x0 |
f x0 x x0 |
||
f x0 |
M |
|
y f |
x |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
y |
f x0 |
|
|
1 |
x x0 |
|
|
|
|
|||
|
|
f |
x0 |
|||
|
|
|
|
|
||
0 |
x0 |
|
|
|
x |
|
|
Рис. 13. |
|
|
|
|
|
54

Нормалью к кривой в точке M x0 , f x0  , принадлежащей
, принадлежащей
графику, называется прямая линия, проходящая через эту точку перпендикулярно касательной. Поскольку угловые коэффициенты перпендикулярно расположенных прямых связаны соотношением
k |
|
|
1 |
, |
то |
уравнение |
нормали, |
проходящей через |
точку |
||||||||
|
|
|
|||||||||||||||
1 |
|
k2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
M x0 , |
f x0 |
, имеет вид |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
y |
f |
x0 |
|
1 |
x |
x0 . |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
f |
x0 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Пример 3.6. Написать уравнение касательной и нормали к |
||||||||||||||||
графику функции y |
3x2 |
5x в точке M 1, |
2 . |
|
|||||||||||||
|
Решение. Так как производная |
y |
6x |
5 в точке x0 |
1 рав- |
||||||||||||
на 1, а значение функции |
y 1 |
2 , то уравнение касательной име- |
|||||||||||||||
ет вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
y |
2 |
1 |
x |
1 |
или y |
x 3 . |
|
||
|
Уравнение нормали имеет вид |
|
|
|
|
|
|||||||||||
|
y |
|
|
2 |
|
1 |
x |
1 или y |
x |
1 . |
|
|
|
||||
|
|
|
1 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3.12. Производные высших порядков явно заданной функции
Производная y f
f  x
x является функцией от x и называется производной первого порядка.
является функцией от x и называется производной первого порядка.
Если функция f  x дифференцируема, то производная от
x дифференцируема, то производная от
производной определена, называется производной второго порядка и обозначается
|
|
d 2 y |
|
d |
|
dy |
|
y |
f x |
|
|
|
|
|
. |
dx2 |
|
dx |
dx |
||||
По аналогии, производной n - го порядка называется производная от производной n 1 - го порядка, т.е.
55

y n
 y n 1
y n 1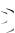
 .
.
Производные порядка выше второго называются производными высших порядков, причем порядок производной обозначается числом в скобках, записанным в виде верхнего индекса.
Пример.3.7. Найти производную 5-го порядка функции y ln x .
|
Решение. y |
|
ln x |
|
1 |
|
, |
|
y |
|
|
1 |
|
|
|
1 |
|
, |
y 3 |
|
2 |
, |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
x |
|
x2 |
|
|
|
|
x3 |
||||
y 4 |
|
2 |
|
|
6 |
, |
y 5 |
|
|
6 |
|
|
24 |
. |
|
|
|
|
|
|
|
|
||||||||
|
|
x3 |
|
|
x4 |
|
|
|
|
|
|
|
|
|
x 4 |
|
|
x5 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
3.13. Формула Лейбница |
|
|
|
|
|
|
|
|
||||||||||||||
|
Предположим, что функции u x |
и v x |
имеют производные |
|||||||||||||||||||||||||||
до n -го порядка включительно. Тогда, |
|
применяя правила диффе- |
||||||||||||||||||||||||||||
ренцирования, получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
u v |
u v u v , |
|
|
u v |
|
|
|
u v 2u v u v , |
|||||||||||||||||||
|
|
|
|
|
|
u v 3 |
|
u v 3u v 3u v u v , … |
|
|
|
|||||||||||||||||||
|
Для производной n -го порядка придем к общей формуле, на- |
|||||||||||||||||||||||||||||
зываемой формулой Лейбница: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
u |
v n |
n Cni u n i v i |
|
u n |
|
v |
n |
u n 1 v |
n n |
1 |
u n |
2 v ... |
||||||||||||||||||
|
1 2 |
|||||||||||||||||||||||||||||
|
|
|
i |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
n n |
|
1 ... n |
|
i |
1 |
u n |
i |
v i ... |
u |
v n . |
|
|
|
||||||||||||
|
|
|
|
|
|
|
1 |
2...i |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Здесь |
Cni |
|
n! |
|
, |
|
|
|
n! |
1 2 |
|
3... n |
2 |
|
n |
1 n , |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
i! n |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
i ! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
n! называется факториалом, является функцией натурального аргумента n и вычисляется как произведение всех натуральных чисел от 1 до n включительно.
56

Пример |
3.8. |
Найти |
производную 5-го |
порядка |
функции |
||||||||||
y x3e2x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. |
v x3 , |
v |
3x 2 , |
v |
6x, |
v |
|
6, |
v 4 |
v 5 0, |
|||||
u e2x , |
u 2e2x , |
u 4e2x , |
u 8e2x , |
u 4 |
16e 2 x , |
||||||||||
u 5 |
32e2x , |
|
5 16e2x 3x2 |
5 4 8e2x 6x |
5 4 3 4e2x 6 . |
||||||||||
x3e2x |
5 |
32e2x x3 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 2 |
|
|
1 2 |
3 |
|
|
|
3.14. Производные высших порядков неявно заданной |
|||||||||||||||
|
|
|
|
|
|
функции |
|
|
|
|
|
|
|
||
Если |
функция |
y |
f |
x |
задана |
неявно |
в |
виде |
уравнения |
||||||
F x, y |
0 , то производная первого порядка получается после диф- |
||||||||||||||
ференцирования по x вышеуказанного уравнения и разрешения его относительно y . Продифференцировав по x первую производную, получим вторую производную от неявной функции, содержащую x, y, y
. Продифференцировав по x первую производную, получим вторую производную от неявной функции, содержащую x, y, y . Подставляя в выражение для второй производной ранее найденное выражение для y
. Подставляя в выражение для второй производной ранее найденное выражение для y , получим зависимость y
, получим зависимость y от x и y .
от x и y .
Пример 3.9. Найти |
y , если xy2 |
y |
1 . |
|
|||
Решение. Продифференцируем левую и правую части уравне- |
|||||||
ния неявно заданной функции по x : |
|
|
|
||||
|
|
|
y2 x 2y y |
y |
0 . |
|
|
|
|
y2 |
|
|
|
||
Отсюда y |
|
|
. Продифференцируем еще раз по x : |
||||
x 2y |
1 |
||||||
y |
|
2y y (x 2y 1) ( y 2 ) (2y x 2y ) |
. |
||||
|
|
|
x 2y 1 |
2 |
|
||
|
|
|
|
|
|
||
Подставляем выражение для y и получаем:
и получаем:
|
2 y |
( y 2 ) |
(x 2 y 1) ( y 2 ) (2 y 2x |
( y 2 ) |
) |
|
||||
y |
(x 2 y 1) |
(x 2 y 1) |
= |
|||||||
|
|
|
|
|
|
|||||
|
|
|
x 2 y |
1 2 |
|
|
|
|||
|
|
|
|
|
|
|
|
|||
|
|
|
|
2 y 3 3xy |
2 |
. |
|
|
|
|
|
|
|
|
2xy 1 3 |
|
|
|
|||
|
|
|
|
|
|
|
|
|||
57

3.15. Производные высших порядков от функций, заданных параметрически
|
|
|
Пусть |
функция y |
|
|
f |
x |
|
задана |
параметрическими |
уравне- |
|||||||||||||||||||||
ниями: x |
x t , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
y |
y t . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Первая производная |
y |
|
находится по формуле y |
|
|
|
yt |
. Рас- |
||||||||||||||||||||||
|
|
x |
x |
xt |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
смотрим новую параметрически заданную функцию: |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
x t , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
yx |
|
|
t . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yt |
|
|
|
|
|
|
|
ytt |
xt |
yt xtt |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
Тогда |
yx |
x |
ytt |
|
|
t |
|
|
|
|
xt |
|
|
|
|
|
|
xt |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
xt |
|
|
|
xt |
|
|
|
|
|
|
xt |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
ytt |
|
xt |
|
|
yt |
xtt |
. |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xt |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
Пример |
3.10. |
|
Найти |
вторую |
|
производную |
функции |
|||||||||||||||||||||||
x |
|
cos 2 t, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
sin 2 t. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. |
yxx |
|
sin 2 t |
|
|
tt |
|
cos 2 t |
t |
|
|
sin 2 t t |
cos 2 t |
tt |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin 2 t t |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
2 sin t cos t t |
|
2 cos t |
sin t |
|
|
2 sin t |
cos t |
2 cos t sin t |
t |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
2 sin t |
cos t |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
2 cos 2 t |
sin 2 t |
2 cos t |
sin t |
|
|
2 sin t |
cos t |
2 |
sin 2 t |
cos 2 t |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 sin t |
cos t |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
58 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
