
Методическое пособие 449
.pdf
6.Приведите примеры алгебраической рациональной функции
иалгебраической иррациональной функции.
7.Какая функция называется сложной? Приведите примеры сложной функции, содержащей две промежуточные функции.
8.Дайте определение монотонно возрастающей функции, ограниченной функции.
9.Может ли нечетная функция иметь область определения
D y : 0, ?
2.ПРЕДЕЛ. НЕПРЕРЫВНОСТЬ ФУНКЦИИ
2.1.Предел функции
Число A называется пределом функции y f x при x ,
стремящемся к а ( x a ), если для любого сколь угодно малого положительного ε > 0 найдется такое δ(ε) > 0, что для всех х, удовлетворяющих неравенству x a выполняется неравенство
f x A . Если A есть предел функции y f x при x a , то пишут
lim f x A .
x a
Определение предела функции y f x графически иллюстрируется следующим образом (рис. 1).
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
А+ |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
А |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
А- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а- |
а |
|
|
а+ |
x |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
Рис. 1 |
|
|
|
|||||
Для сколь угодно малой -окрестности около ординаты |
A |
||||||||||||||||||
найдется такая окрестность точки |
a , что для всех точек |
x |
из |
||||||||||||||||
окрестности точки a точки графика функции |
y f x |
будут |
|||||||||||||||||
10

лежать внутри полосы шириной y A ε, y A ε .
Число A называется пределом функции y f x при мящемся к бесконечности, если для любого сколь угодно малого положительного ε > 0 найдется такое N , что для всех x N будет выполняться неравенство f x A , что записывается следующим образом
Графическая иллюстрация понятия предела функции y f x при x сводится к тому, что какой бы узкой не была бы выбрана
полоса шириной 2 |
около прямой y A, все равно для всех x , на- |
||
чиная с некоторого |
N , график функции не будет выходить за пре- |
||
делы этой полосы |
|
|
|
у |
|
|
|
А |
A+ |
|
|
|
A- |
|
|
О |
|
N |
х |
|
|
Рис. 2 |
|
2.2. Бесконечно малые и их основные свойства |
|||
Функция |
y (x) называется |
бесконечно малой величиной |
|
при x a , если |
lim (x) 0 , т.е. для любого сколь угодно малого |
||
|
x a |
|
|
ε > 0 найдется такое δ(ε) > 0, что для всех x , удовлетворяющих неравенству x a , имеет место неравенство x .
Любая константа, какой бы малой она ни была, не является бесконечно малой величиной.
11

Пример 2.1. Функция 1x будет бесконечно малой при
x , так как lim 1 0 . Действительно, из определения предела
x x
следует, что для любого наперед заданного произвольно малого положительного найдется такое число N, что для всех значений х,
удовлетворяющих неравенству |x|> N, |
1 |
0 |
. Имеем |
1 |
, |
|
x |
x |
|||||
|
|
|
|
| x | |
1 |
, тогда |
N |
1 |
, | x | N |
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
Теорема 1. Если |
lim f x A , то ( f x A ) есть бесконечно |
||||||
x a
малая величина, и наоборот: если f x A x , где x - беско-
нечно малая величина, то lim f x A .
x a
Теорема 2. Сумма конечного числа бесконечно малых величин есть величина бесконечно малая.
Теорема 3. Произведение любого числа бесконечно малых величин есть бесконечно малая величина.
Теорема 4. Произведение бесконечно малой величины и ограниченной функции есть бесконечно малая величина.
Следствие . Произведение бесконечно малой величины на константу есть бесконечно малая величина.
Функция y f x называется бесконечно большой величиной
при x a , если для любого сколь угодно большого числа M найдется такое 0, зависящее от M , что для всех x из - окрестности будет выполняться условие f x M , что записывается следующим образом
lim f x .
x a
Теорема 4. Если x является бесконечно малой величиной,
1
то есть бесконечно большая величина.
x
12
2.3. Основные теоремы о пределах
Рассмотрим пределы функций при x a , полагая, что результаты не изменятся и при x .
Теорема 1. Предел алгебраической суммы функций u x и v x равен алгебраической сумме пределов этих функций.
|
|
lim u x v x lim u x lim v x . |
|
||||||||
|
|
x a |
|
|
|
x a |
|
x a |
|
|
|
Пример 2.2. |
|
|
|
|
|
|
|
|
|
|
|
|
5x2 6x |
|
|
6 |
|
|
6 |
|
|
|
|
lim |
|
lim 5 |
|
|
|
lim 5 lim |
|
5 |
0 |
5 . |
|
x2 |
|
|
|||||||||
x |
x |
|
x |
x |
x x |
|
|
|
|||
Теорема 2. Предел произведения функций u x и v x равен
произведению пределов этих функций. |
|
|
||||
lim |
u x v x lim u x lim v x . |
|||||
x a |
|
|
x a |
x a |
||
Следствие. Постоянный множитель можно выносить за знак |
||||||
предела: |
lim cv x c lim v x . |
|||||
|
||||||
|
x a |
|
|
|
x a |
|
Теорема 3. Предел частного от деления двух функций u x и |
||||||
v x равен частному от деления пределов этих функций |
||||||
|
u x |
lim u x |
||||
|
x a |
|
||||
|
lim |
|
|
|
. |
|
|
|
|
|
|||
|
|
|
|
|
lim v x |
|
|
x a v x |
|||||
|
|
|
|
|
x a |
|
Теорема 4. Если lim f x A , а функция y принимает неотри- |
||||||
|
x a |
|
|
|
|
|
цательные значения |
y 0 , то |
A есть неотрицательное число A 0 |
||||
(без доказательства).
Теорема 5. Если между соответствующими значениями двух функций u u(x) и v=v(x) выполняется неравенство u(x) v(x) и
lim u(x) u0 , |
lim v(x) v0 , то имеет место неравенство u0 |
v0 . |
|
x a |
x a |
|
|
Теорема 6. Если lim u(x) u0 , lim v(x) u0 и выполняется |
|||
|
x a |
x a |
|
неравенство u(x) z x v(x) , то |
lim z(x) u0 . |
|
|
|
|
x a |
|
13
Теорема 7. Если функция |
y f x |
при |
x a |
|
является не- |
||||||||||||||||
|
|
|
|
|
|
f x |
|
M , то |
|||||||||||||
убывающей и ограничена сверху числом |
M , |
т.е. |
|
|
|||||||||||||||||
функция y f x имеет предел при x a . |
|
|
|
|
|
|
|
|
|
|
|||||||||||
Пример 2.3. Вычислить предел |
lim |
7x 2 |
2x |
. |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
lim 7x2 2x |
|
x 1 3x 4 |
|
1 |
|
|
|
|
|
|
|
|
||||
|
|
2 |
2x |
|
|
7 lim x2 2 lim x |
|||||||||||||||
lim |
7x |
|
|
x 1 |
|
|
|
x 1 |
|
|
x 1 |
|
|
9 |
. |
||||||
|
|
|
lim 3x4 1 |
3lim x4 lim 1 |
|
|
|||||||||||||||
x 1 3x4 1 |
|
|
2 |
|
|||||||||||||||||
|
|
|
|
|
x 1 |
|
|
|
x 1 |
|
|
x 1 |
|
|
|
|
|
|
|||
Если при вычислении пределов алгебраической суммы, произведения или частного от деления функций сами функции стремятся к некоторым константам, не равным одновременно нулю в случае деления функций, то вычисление пределов как в предыдущем примере не вызывает затруднения. Пределы отношения бесконечно малых величин, отношения бесконечно больших величин, произведения бесконечно малой и бесконечно большой величины в зависимости от частного закона изменения рассматриваемых величин могут принимать различные значения или даже не существовать. Выраже-
ния вида |
0 |
, |
|
, 0 , , 1 |
называются неопределенно- |
||
|
|
|
|||||
|
|
|
|
||||
|
0 |
|
|
|
|
||
стями.
14
|
|
|
|
2.4. Предел функции |
|
|
sin x |
при x 0 |
|
||||||||||||||||||||||||||||
|
|
|
|
|
x |
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
(первый замечательный предел) |
|
|||||||||||||||||||||||||||||
Функция |
|
y |
sin x |
|
не определена при |
x 0 . Найдем предел |
|||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
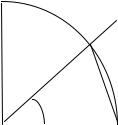
этой функции |
при |
x 0 . |
Рассмотрим |
окружность радиуса R . |
|||||||||||||||||||||||||||||||||
Пусть острый центральный угол MOA равен x (рис. 11). |
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
М |
|
|
|
С |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
О |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Площадь |
|
|
|
треугольника |
|
|
MOA |
|
|
определяется |
формулой |
||||||||||||||||||||||||||
S MOA |
AO MB |
|
|
R R sin x |
|
R2 sin x |
, площадь сектора MOA равна |
||||||||||||||||||||||||||||||
2 |
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Ssekt |
|
R 2 x |
, |
|
|
|
|
площадь |
|
|
|
|
|
|
треугольника |
|
COA |
равна |
|||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
S COA |
|
OA CA |
|
R R tgx |
|
|
R |
2tgx |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
2 |
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Поскольку S MOA Ssekt S COA , то имеем |
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, , , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
R 2 sin x |
|
R 2 x |
|
|
R 2tgx |
. |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||||
Разделим все члены на выражение |
R 2 sin x |
|
|||||||||||||||||||||||||||||||||||
|
|
2 |
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
x |
|
|
|
|
1 |
|
|
. |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin x |
cos x |
|
|
|
||||||||||||||||
15
Перейдем к обратным величинам, воспользовавшись свойствами неравенств,
|
|
|
|
|
|
|
|
|
|
1 |
sin x |
cos x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Так как lim cos x 1, lim1 1, а переменная величина |
|
sin x |
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
x 0 |
|
|
|
|
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
||||
заключена между двумя величинами, имеющими предел равный 1. |
|
|
|
||||||||||||||||||||||||||||||||||||
Следовательно, на основании теоремы 6 предыдущего параграфа |
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
lim |
sin x |
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
x 0 |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Пример 2.4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
lim |
sin 3x |
lim |
sin 3x |
|
|
3 5x |
|
|
3 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
5 sin 5x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
x 0 sin 5x |
x 0 |
3x |
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
Пример 2.5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
2 3x |
|
|
|
|
|
|
|
|
2 3x |
|
|
|
|
|
9x 2 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
1 cos 3x |
|
2sin |
|
|
|
|
|
|
|
sin |
|
|
|
|
|
49x |
2 |
|
|
4 |
|
|
|
9 |
|
|||||||||||||
lim |
lim |
|
|
2 |
|
2 lim |
|
|
|
|
2 |
|
|
|
|
|
|
|
. |
||||||||||||||||||||
sin 2 7x |
|
|
sin 2 |
|
7x |
|
|
3x 2 |
sin 2 7x |
49x 2 |
|
|
98 |
||||||||||||||||||||||||||
x 0 |
x 0 |
|
|
|
|
|
x 0 |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
2.5. Число e. Второй замечательный предел |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Рассмотрим переменную величину 1 |
|
|
|
|
. Можно показать, |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
что эта переменная величина возрастает и ограничена, и, следовательно, она должна иметь предел. Действительно,
|
|
|
1 x |
||
lim 1 |
|
|
|
|
e , |
|
|
||||
x |
|
|
x |
|
|
где e - иррациональное число (e 2,71828...) . |
|||||
Если в равенстве положить |
|
1/x |
=, то при x имеем |
||
0 и получаем |
|
|
|
|
|
lim 1 1/ |
= е. |
||||
0 |
|
|
|
|
|
16
При решении конкретных задач на пределы могут быть полезны модифицированные варианты записи второго замечательного предела:
|
|
|
|
|
|
|
|
|
|
1 |
|
|
x |
|
|
|
|
|
|
|
1 |
|
|
|
x |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
lim 1 |
|
|
|
|
|
|
|
e , |
lim |
|
1 |
|
|
|
|
e , |
|||||||||||
|
|
x |
|
|
x |
|
|
|
|
|
x 0 |
|
x |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где x является бесконечно большой величиной, а x - беско- |
||||||||||||||||||||||||||||||
нечно малой величиной при x a , или при x . |
|
|
|
|
||||||||||||||||||||||||||
Пример 2.6. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
1 x 6 |
|
|
|
|
|
|
|
|
|
1 |
|
x |
|
1 |
6 |
|
|
|
|
|
||||||||
lim |
1 |
|
|
|
= lim |
|
|
1 |
|
|
|
|
1 |
|
|
|
= |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
x |
|
x |
|
x |
|
x |
|
|
|
x |
|
|
|
|
|
|
||||||||||||||
|
|
1 x |
|
|
|
|
|
|
|
1 |
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
= lim 1 |
|
|
|
|
lim |
1 |
|
|
|
|
|
= е 1=е. |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
x |
|
x |
x |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Пример 2.7. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
1 3x |
|
|
|
|
|
|
|
|
|
1 |
|
x |
|
|
1 x |
|
|
1 |
x |
|||||||
lim |
|
1 |
|
|
|
|
= lim |
|
|
1 |
|
|
|
|
1 |
|
|
|
|
1 |
|
|
= |
|||||||
x |
|
|
|
x |
|
x |
|
x |
|
|
|
|
x |
|
|
|
x |
|
||||||||||||
|
|
|
1 |
x |
= lim |
1 |
|
|
|
|
||||
x |
|
x |
||
|
|
|
1 |
x |
|
|
|
1 |
x |
= е е е = |
|
3 |
|
lim |
1 |
|
|
lim |
1 |
|
|
e |
|
. |
|||
|
|
|
|||||||||||
x |
|
x |
x |
|
x |
|
|
|
|
||||
Пример 2.8.
|
x 3 |
x 3 |
|
|
x 1 4 x 3 |
|
|
|
|
4 x 3 |
|
||||||||||||||||
lim |
|
|
|
|
|
|
= lim |
|
|
|
|
|
|
|
|
|
= lim |
1 |
|
|
|||||||
|
1 |
|
|
x 1 |
|
|
|
||||||||||||||||||||
x |
x |
|
|
x |
|
|
|
|
|
|
x |
|
|
x 1 |
|
||||||||||||
|
|
|
|
|
4 |
|
x 1 4 |
|
|
|
|
|
|
|
|
4 |
y 4 |
|
|
|
|
|
|
||||
== lim 1 |
|
|
|
|
|
|
== |
lim |
1 |
|
|
|
= |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
x |
|
|
|
x 1 |
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
4 |
y |
|
|
|
|
|
|
4 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|||
lim 1 |
|
|
|
|
lim |
1 |
|
|
|
= e4 |
1 e4 . |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
y |
|
|
y |
|
y |
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
17
2.6. Раскрытие некоторых неопределенностей
Рассмотрим предел функции lim |
f (x) |
|
(или при x ), кото- |
|
|
||
x a |
g(x) |
||
рый при непосредственной подстановке x |
= a приходит к одному |
||
из случаев неопределенности. Укажем приемы для решения таких примеров, приемы «раскрытия неопределенности».
|
1. Рассмотрим предел отношения многочленов при |
x |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
lim |
Pn x |
, |
|
|
где |
|
|
P |
|
x |
a |
|
|
xn |
|
a |
n 1 |
xn 1 |
|
|
... a |
|
|
x2 a x a |
|
, |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
n |
|
2 |
0 |
||||||||||||||||||||||||||||||||||||||||||||||||||||
x Qm x |
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Q x b xm b |
|
xm 1 |
... b x b |
|
. Для раскрытия получающейся |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
m |
|
|
m 1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
неопределенности |
|
|
|
необходимо вынести x в старшей степени в |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
числителе и знаменателе |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
n 1 |
|
|
|
|
|
|
|
|
a |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
Pn x |
|
|
|
|
|
xn a |
n |
|
|
|
|
... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
xn |
|
|
|
|
|
|
|
|
xn an |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
lim |
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
. |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
x Q |
m x |
|
x |
|
|
m |
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
x xmb |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x |
|
|
b |
|
|
|
m 1 |
... |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
xm |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Если m n , |
то предел равен отношению коэффициентов при |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
старших степенях |
|
an |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
bm |
|
|
|
|
|
|
Pn x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Если же m n |
, то |
lim |
|
lim |
|
|
|
an |
|
|
|
|
|
|
=0. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x Qm x |
|
|
x x m nbm |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P x |
|
|
|
|
|
|
|
|
|
|
xn m a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
В случае n m lim |
|
n |
|
|
|
|
|
= lim |
|
|
|
|
|
|
|
|
n |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
bm |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x Qm x |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
где знак бесконечности определяется знаком коэффициента |
|
an |
|
. |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
bm |
|
|
||||
|
Пример 2.9. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
4 |
|
2 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
7x3 4x2 2x 1 |
|
|
|
|
|
|
|
|
x |
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
x2 |
|
x3 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
lim |
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
. |
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
x 3x3 4x |
2 |
6x 8 |
|
|
x |
|
|
|
3 |
|
|
|
|
4 |
|
6 |
|
|
|
|
8 |
|
|
|
3 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
x2 |
|
|
x3 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
18

|
Здесь было использовано, что при x величины |
1 |
, |
1 |
, |
|
x |
x 2 |
|||
|
|
|
|
||
1 |
стремятся к нулю. |
|
|
|
|
x3 |
|
|
|
|
|
|
|
|
|
|
2. Если в пределе многочлены в числителе и знаменателе
0
стремятся к нулю, то получается неопределенность вида , для
0
раскрытия которой надо разложить числитель и знаменатель на множители и сократить одинаковые бесконечно малые величины.
Пусть a является действительным корнем кратности многочлена в числителе, т.е.
Pn x x a Pn x , где Pn a 0 .
Кроме того, a является действительным корнем кратности
многочлена знаменателя, то есть
Qm x x a Qm x , где Qm a 0 .
Если = , то
|
|
|
|
P x |
|
x a |
P |
|
x |
|
|
|
P |
a |
|
|
|||||||||
|
lim |
|
n |
|
|
lim |
|
|
|
|
|
n |
|
|
|
|
|
n |
|
|
. |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
Qm a |
|
|||||||||
|
x a Qm x |
x a x a Q |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
||
Если , то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
lim |
Pn x |
lim |
|
x a Pn x |
|
|
Pn a |
|
lim x a 0 . |
||||||||||||||||
|
|
|
|
||||||||||||||||||||||
x a Qm x |
|
|
x a x a Qm x |
|
|
Qm a x a |
|
|
|
|
|||||||||||||||
Если , то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
lim |
Pn x |
lim |
x a Pn x |
|
|
|
Pn |
a |
lim |
|
1 |
|
|
. |
|||||||||||
|
|
|
a Qm x |
|
|
|
|
|
|
|
|
|
|||||||||||||
x a Qm x |
|
x a |
x |
|
|
|
Qm a x a x a |
|
|||||||||||||||||
lim
x 3
Пример 2.10. x3 2x2 3x
x2 5x 6
Пример 2.11.
lim |
x(x2 2x 3) |
lim |
x(x 3)(x 1) |
12 . |
|
(x 2)(x 3) |
(x 2)(x 3) |
||||
x 3 |
x 3 |
|
19
