Методическое пособие 276

какого номера) в итоге следующего испытания система перейдет в состояниеj.

Таким образом, в обозначенииpij первый индекс указывает номер предшествующего, а второй − номер последующего состояния. Например, p23 – вероятность перехода из второго состояния в третье.

Пусть число состояний конечно и равноk. Матрицей перехода системы называют матрицу, ко-

торая содержит все переходные вероятности этой системы:

Так как в каждой строке матрицы помещены вероятности событий (перехода из одного и того же состоянияi в любое возможное состояниеj), которые образуют полную группу, то сумма вероятностей этих событий равна единице [1]. Другими словами, сумма переходных вероятностей каждой строки матрицы перехода равна единице:

k

pij 1. i, j 1

Приведем пример матрицы перехода системы, которая может находиться в трех состоянияхA1,A2,A3; переход из состояния в состояние происходит по схеме однородной цепи Маркова; вероятности перехода задаются матрицей:

9

Здесь видим, что если система находилось в состоянииA1, то после изменения состояния за один шаг она с вероятностью 0,5 останется в этом же состоянии, с вероятностью 0,5 останется в этом же состоянии, с вероятностью 0,2 перейдет в состояние A2, то после перехода она может оказаться в состояниях A1,A3; перейти же из состояния A2 в A2 она не может. Последняя строка матрицы показывает нам, что из состояния A3 перейти в любое из возможных состояний с одной и той же вероятностью 0,1.

На основе матрицы перехода системы можно построить так называемый граф состояний системы,его еще называют размеченный граф состояний. Это удобно для наглядного представления цепи. Порядок построения граф рассмотрим на примере.

Пример 2. По заданной матрице перехода построить граф состояний.

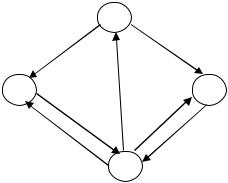
Т.к. матрица четвертого порядка, то, соответственно, система имеет 4 возможных состояния, приведенных на рис. 9.

10

Источник S определяется как множество разбиений Sj с совокупностью всевозможных условных вероятностей элементов разбиений p(Si 0 j 0 | Si 1 j 1 ...Si n j n ) и p(Si j ).

Источник S называется стационарным , если ве-

Si 1 1 ,Si 1 2 …Si n n обычно отождествляются с соответствующими наборами букв ai1, ai2, … , аin и вместо p(Si n j + n /Si 0

j Si 1 j + 1 ...Si n - 1 j n - j 0 ) пишут p(ain/ai0ai1 … аin-1), подразумевая

под этим вероятность появления буквы аin после набора

букв ai0ai1 … аin-1.

Энтропией стационарного источника S называется величина

H(S)=limH(Sп /S1 S2 ...Sn - 1 ).

Стационарный источник S называется источником Бернулли, если p(Si j /Si 1 j 1 Si 2 j 2 ...Si n j n ) = p(S i j ). Другими словами, S — источник Бернулли, если вероятность появления буквы не зависит ни от места в последовательности, ни от предыдущих букв. Для источника Бернулли новое определение энтропии совпадает с определением, использовавшимся ранее [8, 9]:

12

( ) = ( 1) =

= − ∑ ( 1) log ( 1) =

=1

= − ∑ ( ) log ( ).

=1

Стационарный источник S называется Марковским источником r -го порядка, если

p(Si j /Si n j - n Si n - 1 j - n + 1 ...Si 1 j - 1 )= = p(Si j /Si r j - r Si r - 1 j - r + 1 ... Si 1 j - 1 )

при r≤ п. Другими словами, вероятность появления следующей буквы зависит только от r предыдущих. Если S — Марковский источник r-го порядка, то

H(S) =H(Sr+1/S1 S2... Sr) =

= –∑p(Si 1 1 Si 2 2 ...Si r r Si r + 1 r + 1 )log p(Sir+1r+1/Si11

i1…ir+1

Si22...Sirr)=

= –∑p(ai1… аir+1) log p(аir+1/ai1… аir).

i1…ir+1

Пронумеруем подряд все возможные слова из г

13

Можно определить Марковский источник общего вида, состояния которого не связаны с наборами из фиксированного числа букв.

Марковский источник называется эргодическим , если вероятность перехода через произвольное (большее некоторого фиксированного числа т число шагов из каж-

дого состояния si в произвольное состояние sj больше нуля.

Если для некоторого эргодического Марковского источника с п состояниями известны только вероятности перехода из одного состояния в другое, то вероятности его

состояний можно получить из системы уравнений

n

∑ p(Si1) log p(Si1) = p(Si),

j=1

∑ ( ) = 1.

=1

ПустьS — Марковский источник первого порядка с алфавитом {a1, . . ., ak}, и вероятности p(ai/aj) появления буквы щ вслед за буквой ai записаны в матрице Q = {qi j }, гдеqi j =p(ai/aj). Тогда вероятности р (ai ) можно вычислить из уравнения Qp = р , где р = (р(аi), . . . ,р(аk)), учитывая, что ∑ p(ai)=1.

Марковский источник можно полностью задать набором его состояний s1, . . .,sn, матрицей вероятностей перехода из одного состояния в другое p(si / sj) и набором вероятностей порождения букв в каждом из состояний p(a1 / sj ), . . . ,p(ak / sj ), 1 < j < п . Если считать, что последовательности, порождаемые источником, бесконечны только в одну сторону, т. е. имеют начало, то для пол-

14

ного определения источника нужно задать еще начальное состояние.

Разделим бесконечную последовательность букв, порожденную Марковским источникомS с состояниями

на n подпоследовательностей, каждая из которых состоит из букв, порожденных в определенном состоянии sj. Поскольку вероятность появления очередной буквы зависит только от состояния источника, то буквы j-й последовательности появляются независимо друг от друга с вероятностями p(ai/aj). Имея в виду этот факт, говорят, что Марковский источник разделяется на п источников Бернулли, каждый из которых определяется набором условных вероятностей р (a1 /sj ), . . . ,p(ak /sj ), 1 ≤j≤ п, и

обладает энтропией

( ) = − ∑ ( ⁄ ) log ( ⁄ ).

=1

Таким образом, получаем формулу для энтропии

Марковского источника S с состояниями s1, . . .,sn:

( ) =

= − ∑ ( ) ∑ ( ⁄ ) log ( ⁄ ) = − ∑ ( ) ( ).

Таким образом, последовательность, порожденную Марковским источником, можно эффективно кодировать, разделяя ее по числу состояний на п подпоследовательностей и кодируя каждую из них отдельно любым из побуквенных кодов.

Применение Марковских цепей достаточно сильно упрощается, когда эти цепи гомогенны, стационарны и регулярны. Марковская цепь называется гомогенной (однородной), если вероятности переходов между состояниями

15

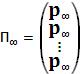
не зависят от выбора временной точки отсчета, т.е. вероятности переходов зависят от разности временных отсчетов.

Гомогенная цепь Маркова является регулярной, ес-

ли[1]:

1. Предельная матрица вероятностей перехода существует.

.

Причем всеn строк предельной матрицы представляют собой предельное распределение вероятностей состояний матрицы.

2. Предельное распределение вероятностей состояний p∞ является единственным стационарным распределением вероятностей состояний любой регулярной цепи Маркова.

p∞ = p0.

3.Цепь Маркова везде будет регулярной, если существует некоторое натуральное значение шага n, при котором все компоненты некоторого столбца матрицы вероятностей перехода на этом шаге n, будет отлично от нуля. Другими словами, цепь Маркова является регулярной если, на некотором шаге n существует по меньшей мере одно состояние, которое может быть достигнуто из любого начального состояния. Если в Марковской цепи вероятность очередного символа оказывает влияние на rпредыдущих символов, то говорят, что память такого источника охватываетr последовательных символов, а сам источник

16

называют конечным дискретным Марковским источником с памятью r.

Заметим, что такой источник обладает свойством и эргодичности. Тогда конечный дискретный эргодический Марковский источник с памятью r полностью считается заданным (или определенным) следующими условиями:

1.Задано непустое множество состояний

{ 1, 2, … , },

причем каждое состояние Si содержит вектор длиной r .

2. Каждое состояние Si соответствует дискретному источнику без памяти с алфавитом Xi = {x1,, x2, … , xM} и вероятностями j-ых символов алфавита

( ) = ( ⁄ ).

3.Задано начальное распределение вероятностей состояний

p0 = (p0(1), p0(2), …, p0(N)).

4.Состояние S[n], образованное из r-1 последовательных символов, после добавления очередного символа X[n] переходит в состояние S[n+1].

Энтропия стационарного эргодического Марковского источника вычисляется исходя из того, что некоторое состояние источникаSi является как бы подисточником без памяти, обладающим в свою очередь соответствующей энтропией. Тогда энтропия первоначального источника равна математическому ожиданию энтропии подисточников. Таким образом, стационарный эргодический Марковский источник с алфавитом из М символов, имеющий n состояний,

17

т.е. N подисточников без памяти энтропия каждого из ко-

торых равна

M

H (X⁄Si) = − ∑ pSi(xm) log2 pSi(xm),

m=1

где pSi(Xm)– вероятность символа Xm при условии Si состояния, обладает энтропией, равной математическому

оживанию энтропии подисточника.

N

H∞(X) = ∑ p∞H(X⁄Si),

i=1

где p∞– предельное распределение вероятностей состояний.

Таким образом, при t→∞ в системе S устанавливается некоторый предельный стационарный режим: хотя система случайным образом и меняет свои состояния, но вероятность каждого из них не зависит от времени и каждое из состояний осуществляется с некоторой постоянной вероятностью, которая представляет собой среднее относительное время пребывания системы в данном состоянии. Это свойство позволяет обходиться при нахождении параметров системы на основе моделирования одной достаточно длинной реализацией.

Для вероятностей p1(t), p2(t),…, pn(t) можно составить систему линейных дифференциальных уравнений, называемых уравнениями Колмогорова, которые в случае нахождения предельных вероятностей превращаются в систему линейных алгебраических уравнений для каждого состояния. Совместно с нормировочным условием эти уравнения дают возможность вычислить все предельные вероятности.

18