Глава 2 автоматизированное проектирование базовых деталей кузнечно-штамповчных машин с применением метода конечных элементов

2.1. Основные понятия метода конечных элементов

Метод конечных элементов (МКЭ) — это численный метод решения дифференциальных уравнений с частными производными, а также интегральных уравнений, возникающих при решении задач прикладной физики. Метод широко используется для решения задач механики деформируемого твёрдого тела, теплообмена, гидродинамики и электродинамики.

Суть метода следует из его названия. Область, в которой ищется решение дифференциальных уравнений, разбивается на конечное количество подобластей (элементов).

В каждом из элементов произвольно выбирается вид аппроксимирующей функции. В простейшем случае это полином первой степени. Вне своего элемента аппроксимирующая функция равна нулю. Значения функций на границах элементов (в узлах) являются решением задачи и заранее неизвестны.

Коэффициенты аппроксимирующих функций обычно ищутся из условия равенства значения соседних функций на границах между элементами (в узлах). Затем эти коэффициенты выражаются через значения функций в узлах элементов.

Составляется система линейных алгебраических уравнений. Количество уравнений равно количеству неизвестных значений в узлах, на которых ищется решение исходной системы, прямо пропорционально количеству элементов и ограничивается только возможностями ЭВМ. Так как каждый из элементов связан с ограниченным количеством соседних, система линейных алгебраических уравнений имеет разрежённый вид, что существенно упрощает её решение.

Если говорить в матричных терминах, то собираются так называемые матрицы жёсткости (или матрица Дирихле) и масс. Далее на эти матрицы накладываются граничные условия (например, при условиях Неймана в матрицах не меняется ничего, а при условиях Дирихле из матриц вычёркиваются строки и столбцы, соответствующие граничным узлам, так как в силу краевых условий значение соответствующих компонент решения известно). Затем собирается система линейных уравнений и решается одним из известных методов.

С точки зрения вычислительной математики, идея метода конечных элементов заключается в том, что минимизация функционала вариационной задачи осуществляется на совокупности функций, каждая из которых определена на своей подобласти, для численного анализа системы позволяет рассматривать его как одну из конкретных ветвей диакоптики — общего метода исследования систем путём их расчленения.

Более подробно суть метода раскроем на конкретном примере.

Монолитная среда нагруженной детали, конструкции или объем деформируемого при штамповке металла разделяется воображаемыми линиями (рис. 31), которые можно рассматривать как стержневые системы.

Рассмотрим силовое нагружение простейшей стержневой системы (рис. 32) .

Составим условия равновесия для узла 1:

(1)

Рис. 31

Рис. 32

Систему уравнений (1.1) можно представить в матричной форме

(2)

где

A= - матрица уравнений равновесия;

- вектор внутренних сил;

- вектор внешних сил (с целью

удобства записи представлен в транспонированной форме)

Рассмотрим аналогичную стержневую систему в деформированном от внешних усилий состоянии (рис.33) , где показаны деформации системы при смещении узла 1 на U и V .

Рис. 33

Стержневая система, соединенная в узлах, должна оставаться соединенной в этих же узлах, и после деформации. Уравнения, выражающие это положение, называются уравнениями совместности:

(3)

или

(4)

или

, (5)

где - матрица уравнений совместности;

 вектор перемещений;

- вектор деформаций.

Из теории матричного исчисления известно, что матрицей, транспонированной по отношению к матрице А, называется матрица А ^Т, столбцами которой являются строки матрицы А, т.е.

(6)

В строительной механике данное соотношение доказывается исходя из того принципа, что на основании закона сохранения энергии работа внешних сил А_p переходит в потенциальную энергию деформации П

(7)

или

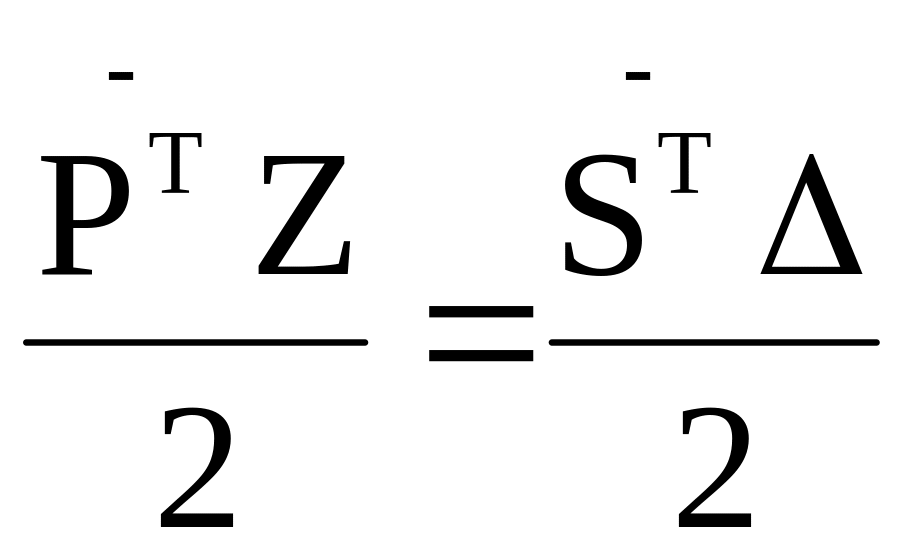(8)

Выражая из (2) вектор , а из (5) вектор получим (6) . Таким образом, матрицы уравнений равновесия и уравнений совместности являются взаимно транспонированными.

Если нагружение рассматривать в зоне упругой деформации, то можно составить физические уравнения, устанавливающие связь между усилиями и деформациями в соответствии с законом Гука для стержневых систем.

, (9)

где ;

- удлинение j-го стержня;

- угол поворота сечения j-го стержня в его начале;

- угол поворота сечения j-го стержня в его конце;

Е – модуль упругости материала стержня;

F_j – площадь поперечного сечения j-го стержня;

J_j – момент инерции сечения j-го стержня;

M_hj, M_kj – моменты, действующие в начале и в конце стержня.

Соотношение (9) справедливо для одного стержня.

Придавая индексу j значение j=1, 2, 3, …, m, то получим соотношение Гука для всей стержневой сиcтемы и которое в матричной форме имеет вид:

, (10)

где матрица В называется матрицей податливости и имеет квазидиагональную структуру

(11)

где b j – блоки (см. форм.9).

Таким образом, получена система уравнений

(12)

Используя граничные условия, которые могут быть заданы перемещениями (кинематические) или напряжениями (статические) методом последовательного исключения система уравнений может быть решена, т.е. определены усилия в стержнях.