2.2. Принцип расчета монолитных конструкций мкэ

Совершенствование электронно-вычислительной техники позволило быстро решать сложные системы уравнений, которые возникают при переходе от стержневых элементов к сплошным (континуальным) системам в виде пластин, оболочек, объемных конструкций.

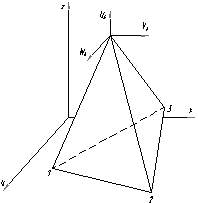
При решении объемной задачи монолитное тело рассчитываемой детали может быть разбито на конечные элементы в виде пирамид, призм, параллелепипедов и т.д. Рассмотрим элемент в виде пирамиды (рис. 34).

Результатом расчета должно явиться определение силового воздействия в узлах элемента, т.е. определение матрицы реакций или матрицы жесткости – R.

Для построения матрицы жесткости необходимо задаться полем перемещений и выразить его через перемещения узловых точек треугольника.

Обычно поля перемещений задают в виде полиномов, число коэффициентов которых равно степеней свободы – i.

Рис. 34

В данном случае для пирамиды i = 4 , тогда

(13)

или в матричной форме



или

, (15)

где ;

.

Считая выбранный элементарный объем бесконечно малым, зависимости между компонентами перемещений (U,V,W) и компонентами линейных деформаций определяются уравнениями Коши:

(16)

Дифференцируя соотношение (2.3) с использованием уравнений Коши, получим

, (17)

где В - матрица, получаемая из матрицы L(x,y,z) путем дифференцирования.

Для континуальных сред в виде пластин, объемных тел закон Гука имеет вид:

(18)

Решая систему (18) относительно x, y, z,  xy,  yz,  zx и записывая результат в матричной форме, получим:

, (19)

где D - блочная матрица

(20)



Выше отмечалось, что на основании закона сохранения энергии выполняется равенство (7) , т.е.

(21)

В данном случае работа внешних сил описывается соотношением

(22)

где - силы, действующие на элемент.

(23)

где K - матрица жесткости, симметричная, ленточного вида.

Таким образом

(24)

Выражение для потенциальной энергии

(25)

Подставляя в (25) зависимости (17), (19) и учитывая, что выражение (15) от координат (x, y, z) не зависит, получим

(26)

На основании (1.7) , приравнивая зависимости (21) и (24) имеем

(26)

Тогда

(27)

Решение интеграла (2.16) с учетом граничных условий может быть выполнено на ЭВМ итерационным методом, в результате чего определяется напряженное состояние объемного элемента.

Проходя поэлементно всю структуру монолитной конструкции, получают объемную картину напряженного состояния детали в любой ее области.

В приложении 1 (П.1) показано распределение эквивалентных напряжений и деформаций по телу шатуна пресса , причем зоны напряжений каждого уровня окрашены соответствующим цветом .