2. Задачи с параметрами

Пример 1. Решим уравнение:

Уравнение – линейное уравнение. Качественное изменение уравнения происходит при тех значениях а, при которых коэффициент при x обращается в ноль. То есть, контрольные значения параметра:

1. При а =0 уравнение примет вид:

Это уравнение не имеет решений.

2. При а =1 уравнение имеет вид:

Это уравнение имеет бесконечно много решений, решение – любое xR.

3. Если а 0, а 1, то уравнение имеет единственное решение:

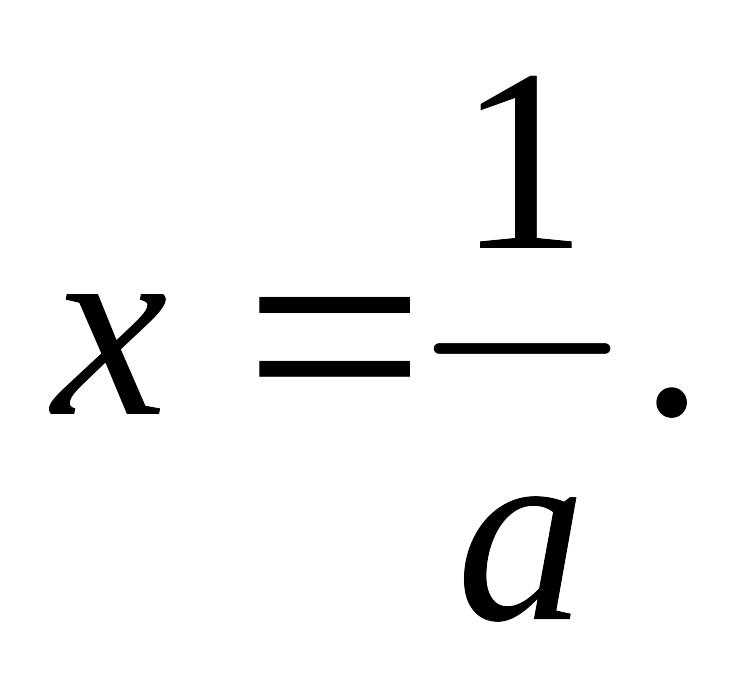
Ответ: При а=0 уравнение не имеет решений. При а=1 уравнение имеет решением любое xR. При а0, а1 уравнение имеет единственное решение

Пример 2. При каких значениях а уравнение: имеет равные корни?

Квадратное уравнение имеет равные корни, если его дискриминант равен 0, то есть:

Ответ: Уравнение имеет равные корни при а=2 и а=

Пример 3. Найдите все значения параметра , при каждом из которых множество решений неравенства содержит какой-нибудь отрезок длиной 2, но не содержит никакого отрезка длиной 3.

1. Проведем равносильные преобразования. ,

, , , , .

2. Так как , то и должны быть противоположных знаков, т.е. получаем систему , равносильную исходному неравенству. При и при множество решений – это интервал . При множество решений – это объединение двух интервалов.

3.  Интервал содержит отрезок длины 3. Значит, и не удовлетворяют условию задачи.

Если , то в интервале , длина которого больше 3, есть отрезок длиной 3 и такие не удовлетворяют условию задачи. Если , то в интервале , длина которого больше 3, есть отрезок длиной 3 и такие не удовлетворяют условию задачи.

4. Если (если ), то длины интервалов и не больше 3. Поэтому в них нет отрезков длиной 3. При этом длина интервала (длина интервала ), больше 2. Поэтому в них есть отрезок длиной 2 и, значит, такие удовлетворяют условию задачи. Если же , то в объединении нет отрезков длиной 2, так как длины этих интервалов равны 2. Значит, не удовлетворяет условию задачи.

Пример 4. При каких значениях а выражение не равно нулю ни при каких значениях х?

Переформулируем задание: найти а, при которых уравнение не имеет решения?

Выполним тождественные преобразования и приведем уравнение к квадратному относительно :

; ;

; .

Полученное уравнение не имеет решения, если дискриминант отрицательный:

; ; . Ответ: .

Пример 5. Найти все целые значения параметра а, при которых неравенство

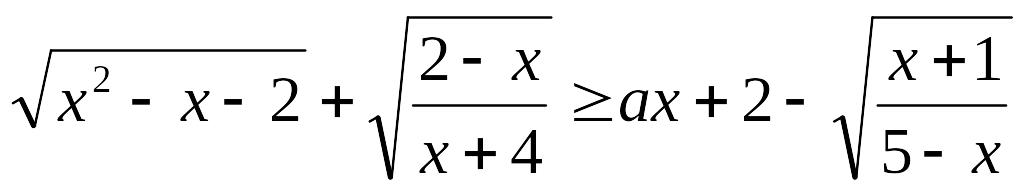не имеет решений.

Найдем область определения неравенства:

.

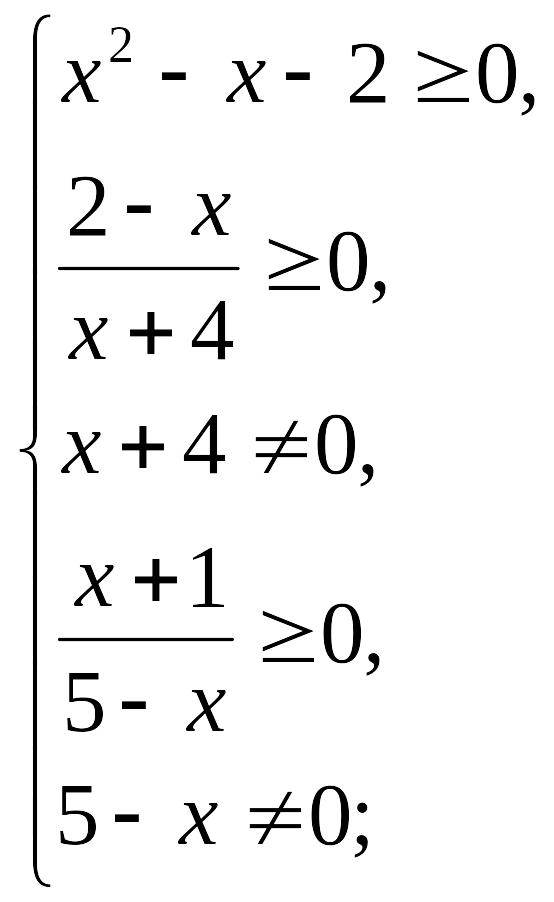
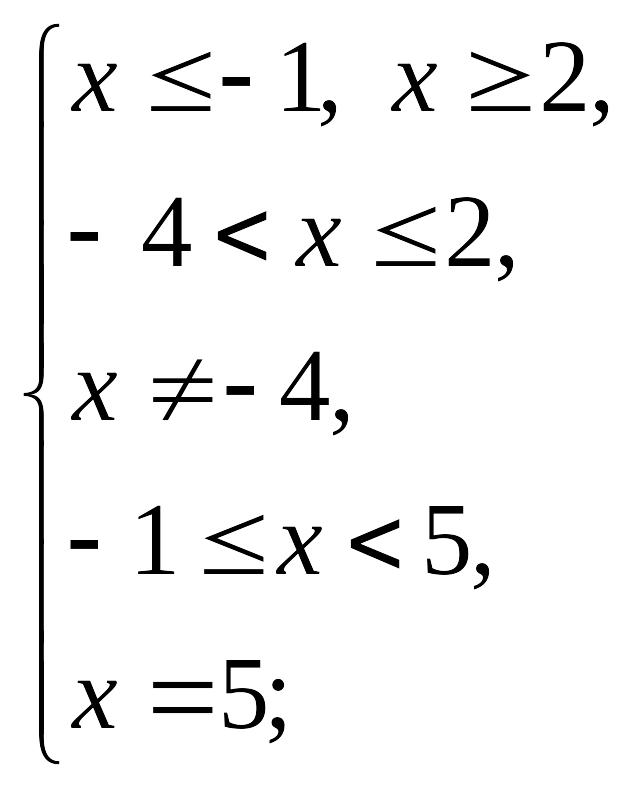
Найдем значения а, при которых - не является решением данного неравенства.

Пусть - решение данного неравенства. Это значит, что , т.е. . Следовательно, при не является решением.

Теперь найдем те значения а, при которых не является решением данного неравенства. Это значит, что , т.е. . Следовательно, при не является решением.

Найдем те значения а, при которых и и не являются решениями данного неравенства. Это . Целыми значениями а из полученного интервала является .

Ответ: .

Пример 6. Исследовать сколько решений имеет уравнение

в зависимости от значений параметра a .

Рассмотрим две равносильные записи уравнения: исходную и

.

Им отвечают свои геометрические образы. Осуществим реализацию геометрического подхода к решению уравнений с параметром в каждом случае.

На рис. 3 приведены графики функций и . Функция определяет семейство параллельных друг другу прямых L с угловым коэффициентом . При изменении a от до некоторого значения , при котором прямая L₁ проходит через точку А, графики функций и не пересекаются и соответственно уравнение не имеет решения. В точке А: , откуда .

Таким образом, при уравнение (5) не имеет решений, при имеет одно решение .

При дальнейшем увеличении параметра а прямая L: будет пересекаться с графиком функции

• в 2 точках при

• в

  .

  3 точках при (прямая L проходит через начало координат) и при (прямая L проходит через точку B – является касательной к графику функции );

• в 4 точках при ;

• в 2 точках при .

Найдем оставшееся единственное неизвестное значение параметра . Из условия касания графиков функций и в точке B имеем

Итак, при - уравнение не имеет решений; Рис. 3

- одно решение;

- два решения;

- три решения;

- четыре решения.