Радианное и градусное измерение углов

В окружности радиусы ОА и ОВ проведены так, что длина дуги АВ равна R (рис. 6). Центральный угол - угол в один радиан (1рад≈57⁰17^' 45^"):

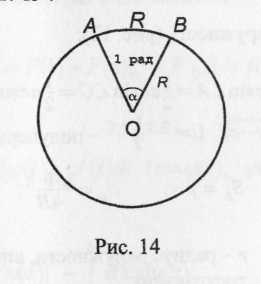
Рис. 6

если α⁰- величина угла в градусах, а, β - в радианах, то

Окружность и круг (рис. 7):

С - длина окружности, С = 2πr;

S_kp - площадь круга, S_kp= πr².

Длина дуги (рис. 7):

Площадь сектора (рис. 7):

Площадь сегмента (рис. 7):

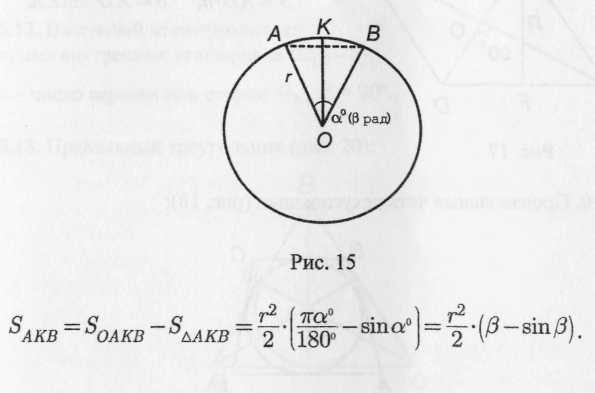
Рис. 7

Параллелограмм (рис. 8):

Рис . 8

Ромб (рис. 9):

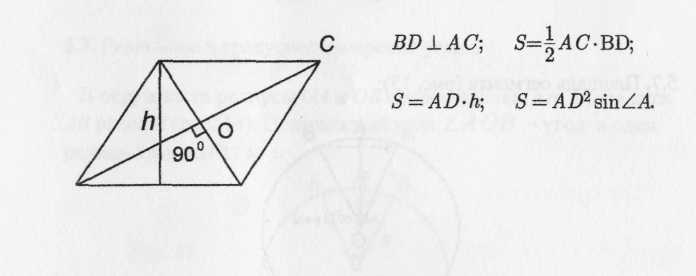
AB=BC=CD=AD

Рис. 9

Произвольные четырехугольники (рис. 10):

Рис. 10

Для четырехугольника, описанного около окружности:

AD+BC=AB+CD

Для четырехугольника, вписанного окружность:

Трапеция (рис.11):

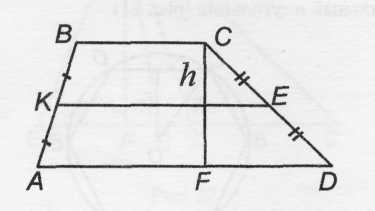
Рис. 11

Выпуклый многоугольник:

сумма внутренних углов равна

n – число вершин или сторон a_n, d=90⁰.

Правильный треугольник (рис.12):

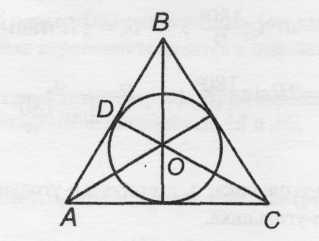
Рис. 12

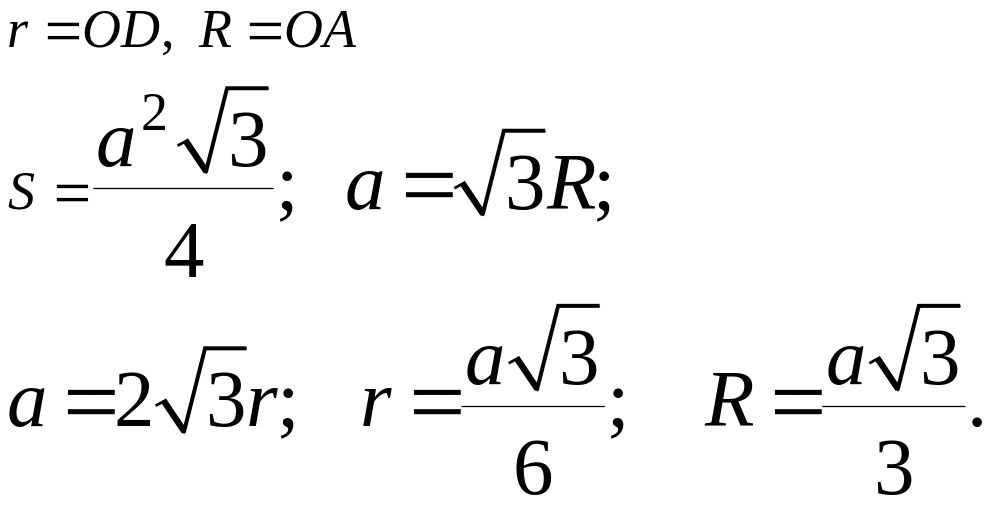
Правильный п - угольник (рис. 13)

Рис. 13

S_n – площадь n – угольника; a_n – сторона n – угольника;

Р_n – периметр n – угольника.

Некоторые соотношения в произвольном треугольнике (рис.14):

Рис. 14

Медиана в точке пересечения делятся в отношении 2:1, начиная от вершины.

Биссектриса угла А делит сторону ВС на отрезки ВЕ и ЕС, пропорциональные боковым сторонам АВ и АС.

Объем прямоугольного параллелепипеда (рис. 15)

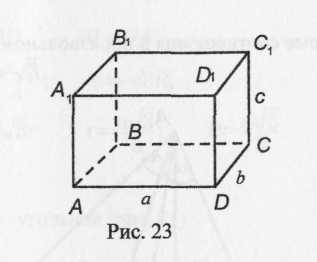
Рис. 15

Объем призмы (рис. 16):

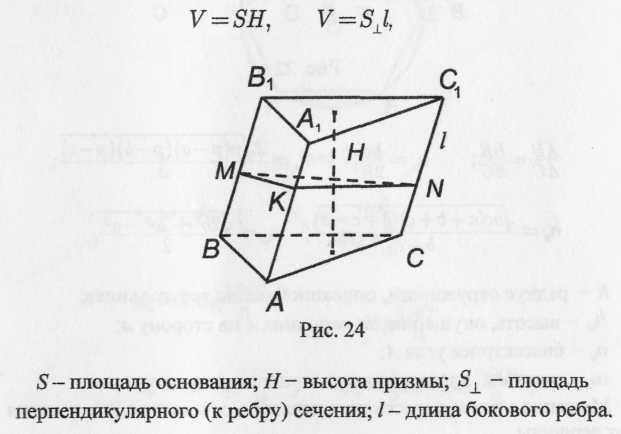
Рис. 16

S – площадь основания; Н – высота призмы; - площадь перпендикулярного (к ребру) сечения; l – длина бокового ребра.

О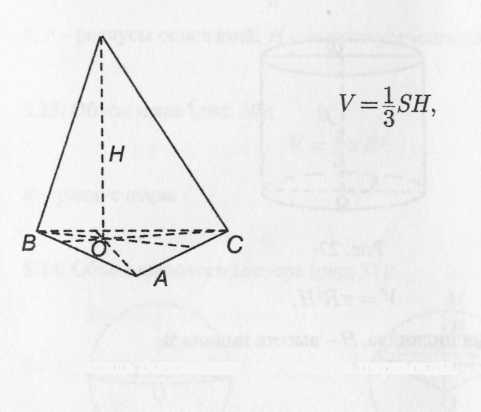 бъем пирамиды (рис. 17):

S − площадь основания;

Н — высота пирамиды.

Рис. 17

Объем усеченной пирамиды (рис. 18):

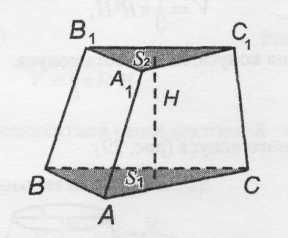
Рис. 18

S₁, S₂ – площади оснований; Н – высота пирамиды.

Объем цилиндра (рис. 19):

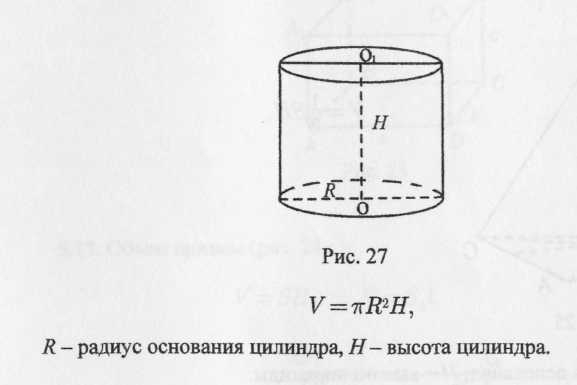
Рис. 19

R – радиус основания цилиндра, Н – высота цилиндра.

Объем конуса (рис. 20):

Рис. 20

R – радиус основания конуса, Н – высота конуса.

Объем усеченного конуса (рис.21):

Рис. 21

R,r – радиусы оснований, Н – высота усеченного конуса.

Объем шара (рис.22):

R – радиус шара.

Объем шарового сектора (рис.23):

Рис. 22 Рис. 23

Н = МО₁ - высота сегментной части сектора; R =ОМ- радиус шара.

Объем шарового сегмента (рис. 24):

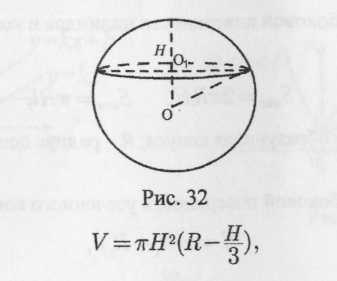
Рис. 24

H = МО₁ - высота шарового сегмента; R =ОМ - радиус шара.

Площадь боковой поверхности призмы:

l - длина бокового ребра; - периметр перпендикулярного сечения.

Площадь боковой поверхности правильной пирамиды:

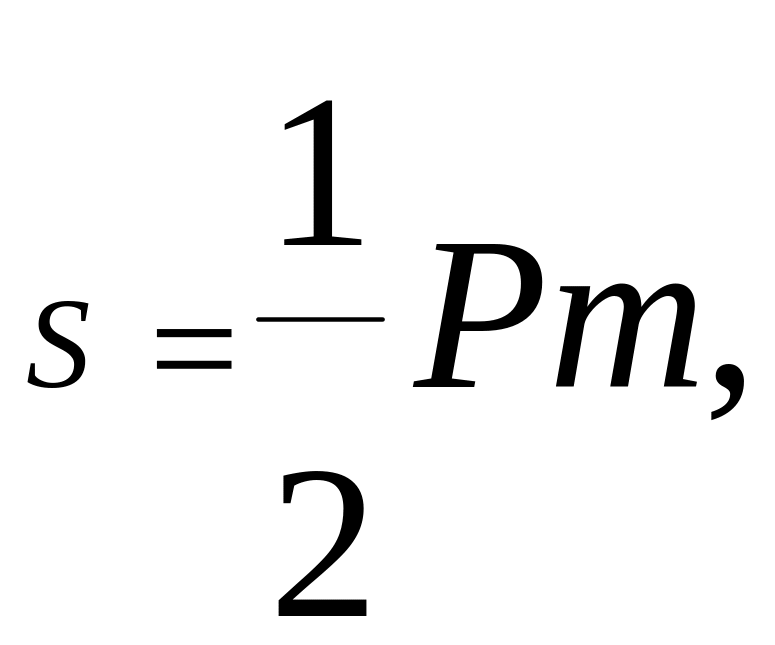
Р - периметр основания; m - высота боковой грани (апофема).

Площадь боковой поверхности правильной усеченной пирамиды:

где P₁, P₂ - периметры оснований; h - высота боковой грани (апофема).

Площадь боковой поверхности цилиндра и конуса (рис 19, 20)

Н - высота; l - образующая конуса; R - радиус основания.

Площадь боковой поверхности усеченного конуса (рис. 21):

l – образующая усеченного конуса; R₁, R₂, - радиусы оснований.

Площадь поверхности сферы:

- радиус сферы.

Площадь сферического сегмента:

R - радиус шара; Н- высота сегмента.

3.2. Решение задач

Задача 1. Какое наибольшее количество точек можно выбрать в круге радиуса 1 так, чтобы расстояние между любыми двумя было бы больше 1;

Предположим, что точек не менее 6. В этом случае никакая из этих точек не может совпадать с центром круга, так как тогда все остальные находились бы от нее на расстоянии не более 1. Соединим центр О круга со всеми шестью точками А₁, А₂, …, А₆ и заметим, что проведенные отрезки не содержат внутри себя ни одну из этих точек А_к . Хотя бы один из центральных углов А_iOA_j не превосходит 60⁰. Тогда в треугольнике А_iOA_j сторона А_iA_j не самая длинная, и поэтому А_iA_j≤ А_iO ≤ 1 или А_iA_j ≤ А_jO≤1.

Итак, число точек с нужным свойством не превосходит 5. Пять точек можно расположить в вершинах правильного пятиугольника, вписанную в данную окружность. Сторона такого пятиугольника больше стороны правильного шестиугольника, а значит, больше 1.

Задача 2. На стороне АВ треугольника АВС выбрана точка D, а на стороне ВС этого треугольника точка Е. Отрезки АЕ и CD пересекаются в точке F. Площади треугольников ADF, AFC FEC равны соответственно S₁ , S₂ и S₃, а площадь четырехугольника FDBE равна S₄. Известно, что среди четырех чисел S₁ , S₂ , S₃, S₄ три равны между собой. Найдите все возможные значения отношения S₁/S₂.

Искомое отношение может принимать одно из трех значений:1, 1/3, .

Пусть AD/DB = 1: a, CE/EB = 1: c, AF/ FE = x, CF/ FD = y. Считая a и c заданными, найдем x и y.

По теореме Менелая для треугольника АВЕ и прямой C-F-D имеем:

,

откуда

x = (1+c)/a.

Аналогично по теореме Менелая для треугольника CBD и прямой A-F-E получаем, что

y = (a +1)/c.

Отметим, что искомое отношение площадей равно 1/у, так как S₁/S₂ = DF/FC = 1/y.

Выразим все интересующие нас площади через площадь треугольника АВС, которую мы можем считать равной 1. Имеем:

Аналогично получаем, что

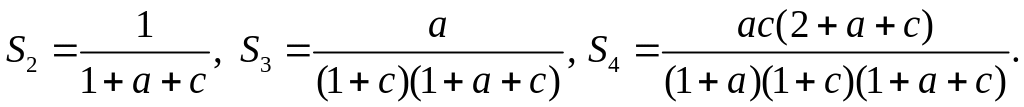
Рассмотрим несколько случаев.

1. Равенство S₁ = S₂ = S₃ невозможно, так как из системы

получим, что а+1 = с, с+1 = а, откуда а+2 = а.

2. Пусть S₁ = S₂ = S₄. Из равенства S₁ = S₂ получаем, что с = 1 + а. Из второго равенства S₁ = S₄ следует, что а(2 + а + с) = 1 + с. Переходя к одной неизвестной, находим, что а = и с = . Наличие положительных решений показывает, что этот случай возможен. В данном случае искомое отношение равно 1.

3. Пусть S₁ = S₃ = S₄. Из равенства S₁ = S₃ получаем, что а² + а = с² + с или

(а-с)(а+с+1)=0.

Так как вторая скобка положительна, то а = с. Из равенства S₁ = S₄ при а = с легко следует, что а = с = 1/2 и поэтому в рассматриваемом случае S₁ / S₂ = 1/3.

4. Если S₂ = S₃ = S₄, то аналогично тому, как мы это делали при рассмотрении случая 2), находим, что а = /2, с = /2 и S₁/S₂ = .

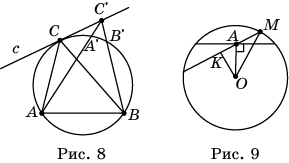
Задача 3. Внутри окружности с центром O дана точка A, отличная от O. Найдите на окружности точку M, для которой угол AMO наибольший.

П

Рис. 25

усть M – произвольная точка окружности, OK – перпендикуляр, опущенный из точки O на прямую MA (рис. 25). В прямоугольном треугольнике KMO гипотенуза OM постоянна (равна радиусу), следовательно, угол AMO тем больше, чем больше катет OK. Поэтому угол OMA будет наибольшим, когда угол OAM – прямой.

Задача 4. В треугольной пирамиде SABC основание – АВС – прямоугольный треугольник с прямым углом при вершине С и острым углом  при вершине А. Боковые ребра пирамиды равны l, и образуют с основанием угол . Найдите объем пирамиды и объем вписанного в нее шара.

1. Начнем с чертежа. По условию все боковые ребра пирамиды равны, поэтому, по теореме 1, основание высоты пирамиды (точка Н) является центром описанной окружности основания (треугольника АВС). Так как АВС прямоугольный, то Н – середина гипотенузы АВ. Таким образом, высота пирамиды лежит в грани SAC, и эта грань перпендикулярна основанию.

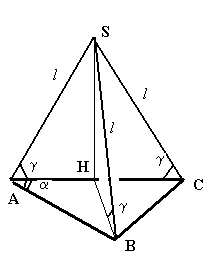
2. Для вычисления объема по формуле нам нужно найти и площадь АВС.

а) из SAH (прямоугольный) ; Рис. 26

б) из того же треугольника , поэтому ;

в) площадь прямоугольного треугольника АВС через гипотенузу и острый угол выражается по формуле . Поэтому = , отсюда  .

3. Чтобы найти объем вписанного шара, нужно знать его радиус ( ). Найдем радиус . Для этого нужно найти площади граней:

= (из пункта 2)

= = .

Так как в АВС: ВС = АС = ; АВ = АС , а SAB и SBC – равнобедренные, то их площади легко вычислить:

; . Таким образом, + ), откуда . Сократив и упростив, получим:

О

бъем предлагаем найти самостоятельно.

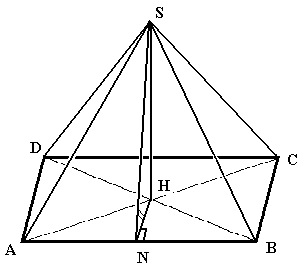
Задача 5. Основание пирамиды SABCD – ромб со стороной а и острым углом при вершине А, равным 60. Боковые грани пирамиды составляют с основанием равные углы  ( = ). Найдите площадь поверхности шара, вписанного в эту пирамиду. Рис. 27

1. Основание высоты SH пирамиды является центром окружности, вписанной в основание. То есть Н – точка пересечения диагоналей ромба. Чтобы изобразить угол  , проведем из точки Н перпендикуляр к стороне АВ. SNH – искомый. Радиус вписанного шара равен: .

2

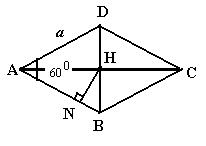
) Найдем : на рис 28. изображен ромб ABCD. Его площадь равна:

Рис. 28

, а периметр Р = 4а. Так как HN – радиус вписанной окружности, то

= .

3) Для вычисления используем формулу . По условию  , поэтому .

4) Теперь найдем r : 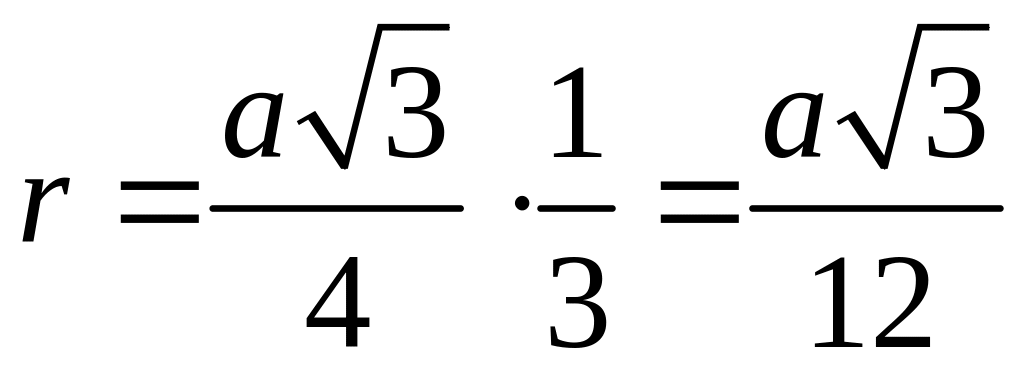, и площадь поверхности вписанного шара  .

Задача 6. В правильной четырехугольной призме построены два параллельных сечения. Первое проходит через середины двух смежных сторон основания и центр симметрии призмы, второе делит ось призмы в отношении 1 : 3. Найдите, как относятся площади этих сечений.

Рис. 29

Сечения изображены на рисунке 29. Так как они параллельны, то площади их ортогональных проекций на основание относятся так же, как площади самих сечений. (Действительно, если  - угол сечения с основанием, S₁ и S₂ –площади сечений, а и - площади их проекций, то) , и ). Считая, что сторона основания равна а, легко посчитать, что , а . Поэтому .

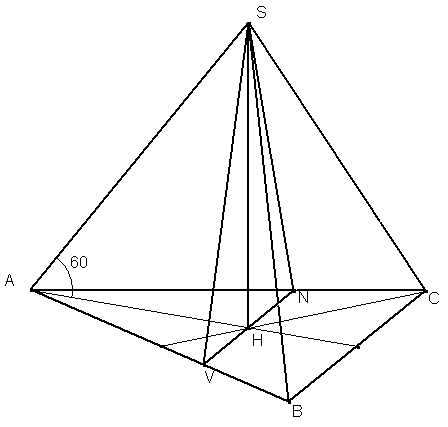Задача 7. Высота правильной треугольной пирамиды равна , а боковое ребро наклонено к плоскости основания под углом 60⁰. Секущая плоскость параллельна стороне основания и содержит высоту пирамиды. Найдите площадь сечения.

Рис. 30

Решение. Заметим, что треугольники AVN и ABC подобны, и коэффициент подобия равен отношению отрезка AH – медианы меньшего треугольника, к медиане большего треугольника. А так как точка H – суть, точка пересечения медиан треугольника ABC, то . Отсюда , где a – сторона основания пирамиды

3) Выразим теперь сторону основания a пирамиды через ее высоту и угол между боковым ребром и основанием. Из прямоугольного треугольника SHA найдем AH: Так как AH – две трети медианы треугольника ABC, а медиана равна , то , а . Осталось найти площадь сечения:

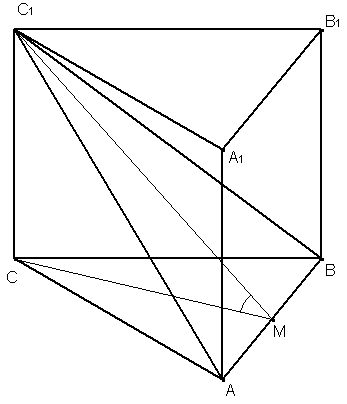Задача 8. В основании прямой призмы лежит равнобедренный прямоугольный треугольник, Плоскость ABC₁ наклонена к плоскости основания под углом 60⁰. Найдите объем призмы.

Решение. Заметим, что линейный угол того двугранного угла, о котором идет речь в условии – это угол C₁MC. Здесь точка M – середина стороны AB, а так как , то CM еще и высота. C₁M

Рис. 31 перпендикулярна AB по теореме о трех перпендикулярах.

Нетрудно заметить, что , а . Рассмотрев прямоугольный треугольник C₁MC с углом 60⁰, найдем CC₁:

Вычислим объем призмы:

.

Задача 9. Объем конуса равен , а радиус основания равен 4. Сечение, проходящее через вершину конуса S, пересекает окружность его основания в точках А и В. Расстояние от центра основания конуса до плоскости сечения равно . Найдите градусную меру угла наклона плоскости сечения SАВ к плоскости основания конуса.

Выполним чертеж. Самое главное – правильно определить расстояние от секущей плоскости до центра основания: Если SM – медиана треугольника SAB, то ОМ и SM перпендикулярны АВ, поэтому плоскость SOM перпендикулярна FD (признак перпендикулярности прямой и плоскости!!!). Но так как АВ лежит в секущей плоскости, то плоскость SOM перпендикулярна также и к ней. Опустив из О перпендикуляр на линию SM пересечения этих плоскостей, мы п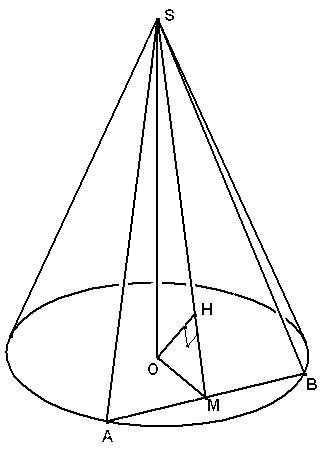 остроим перпендикуляр к сечению из точки О. Поэтому .

2) Заметим также, что нам нужно найти угол OMH, обозначим его . Тогда угол OSH=90⁰-. 3) Так как , то высота конуса равна В прямоугольном треугольнике SOH: 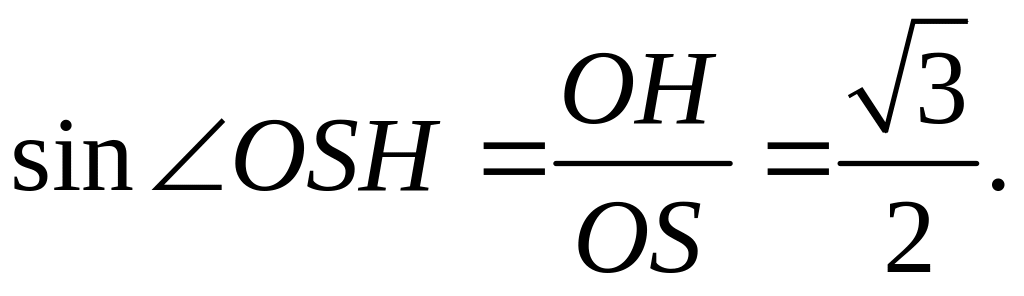Рис. 32 Поэтому данный угол равен 60⁰, но тогда угол =30⁰.

Задача 10. Концы отрезка KP лежат на окружностях оснований цилиндра. Высота цилиндра равна 16, радиус основания равен 10, а угол между прямой KP и плоскостью основания цилиндра равен 45⁰. Найдите расстояние между осью цилиндра и параллельной ей плоскостью, проходящей через точки K и P.

Так как ось цилиндра параллельна сечению, то расстояние от оси до сечения равно длине перпендикуляра, опущенного из любой точки прямой на п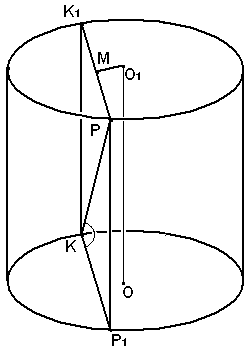 лоскость. В нашем случае удобно взять точку О₁, тогда искомый перпендикуляр – отрезок О₁М, где точка М – середина отрезка K₁P.

Сечение – прямоугольник, а диагональ составляет

Рис. 33 со стороной угол 45⁰, то сечение – квадрат. Таким образом, нам нужно вычислить расстояние от центра окружности, радиусом 10 до хорды этой окружности, равной 16. Иными словами, задача свелась к вычислению высоты равнобедренного треугольника O₁PK₁. Легко вычислить, что она равна 6.

Задача 11. Около правильной треугольной призмы описан цилиндр. Площадь боковой поверхности цилиндра равна 14. Расстояние от оси цилиндра до диагонали боковой грани призмы равно . Найдите объем призмы.

Поскольку цилиндр описан около правильной призмы , то центры О и О₁ ее оснований являются центрами оснований описанного ц илиндра, а радиус цилиндра равен радиусу

Рис. 34 окружности, описанной около основания призмы, то есть около правильного треугольника АВС. Так как призма правильная, то ее боковое ребра АА₁, ВВ₁ и СС₁ перпендикулярны плоскости оснований призмы. Поэтому и ось цилиндра ОО₁ перпендикулярна плоскости АВС. Следовательно, , и по признаку параллельности прямой и плоскости . Из определения расстояния между скрещивающимися прямыми следует, что расстояние между прямой ОО₁ и прямой СВ₁ есть длина перпендикуляра, опущенного из точки О на грань ВСС₁В₁.

Пусть АМ – высота треугольника АВС, то есть АМВС. Тогда центр О треугольника АВС лежит на АМ. Так как ВВ₁АВС, то АМВВ₁. Следовательно, ОМСВВ₁, то есть расстоянием между скрещивающимися прямыми ОО₁ и СВ₁ является длина отрезка ОМ – радиуса окружности, вписанной в основание призмы.. Значит, . Тот же результат получим, рассматривая любую диагональ любой боковой грани призмы.

Треугольник АВС – правильный. Следовательно, , то есть радиус R цилиндра равен ОА. Если Н – высота цилиндра, площадь его боковой поверхности . Отсюда . Следовательно, . Так как цилиндр описан около призмы, то высота призмы равна высоте цилиндра. Объем призмы . Основание призмы – правильный треугольник АВС и R – радиус его описанной окружности, значит, =36 , то есть. Отсюда получаем объем призмы: .

Задачи для самостоятельного решения.

1. а) докажите, что если в основании пирамиды лежит ромб, а все ее боковые ребра равны, то ромб является квадратом.

б) докажите, что если основание пирамиды – прямоугольник, и все его грани одинаково наклонены к основанию, то основание – квадрат.

2. Основание наклонной призмы – правильный треугольник со стороной а. Боковые ребра составляют с основанием угол . Найдите площадь ортогонального сечения призмы.

3. Основание пирамиды SABCD – трапеция диагональ, которой (АС и DB) образуют с боковыми сторонами (CD и AB) прямые углы. Боковые ребра пирамиды равны l, а стороны BC и AD - a и b – соответственно. Найдите: а) объем пирамиды; б) радиус описанной сферы.

4. В правильной треугольной пирамиде боковые грани образуют попарные двугранные углы, величины которых равна  . Какие углы образуют боковые грани с плоскостью основания?

5. В правильной треугольной призме со стороной основания, равной 2 проведено сечение ( , , ). , , а площадь . Найдите длину отрезка .

6. Боковые ребра четырехугольной пирамиды равны 1. Каков ее максимальный объем?

7. Четыре одинаковых шара радиуса r касаются друг друга. Найдите радиус сферы, которой эти шары касаются внутренним образом.

8. Три одинаковых шара радиуса r лежат на плоскости и касаются друг друга. Найдите радиус четвертого шара, который касается трех данных и плоскости, на которой они лежат.

9. Основание прямой призмы KMTK₁M₁T₁ – треугольник KMT в котором . Плоскость KMT₁ наклонена к основанию под углом 45⁰. Найдите площадь боковой поверхности призмы.

10. Секущая плоскость проходит через высоту правильной треугольной пирамиды параллельно стороне основания. Боковое ребро пирамиды наклонено к плоскости основания под углом 30⁰ и равно 4. Найдите площадь сечения.

11. Угол между секущей плоскостью, проходящей через вершину конуса, и плоскостью основания 45⁰. Сечение конуса – прямоугольный треугольник. Найдите площадь сечения, если расстояние от центра основания конуса до секущей плоскости равно 3.

12. Сторона основания правильной четырехугольной пирамиды равна 4, апофема - . Секущая плоскость проходит через сторону основания и делит боковое ребро пополам. Найдите тангенс угла между плоскостями основания и сечения пирамиды.

13. Прямая пересекает окружности оснований цилиндра в точках B и D и наклонена к плоскости основания под углом 30⁰. Плоскость, содержащая прямую BD, параллельна оси цилиндра и удалена от этой оси на расстояние 3. Найдите высоту цилиндра, если радиус его основания равен 6.

14. Все грани призмы ABCDA_1­B₁C₁D₁ – равные ромбы. Углы BAD, BAA₁ и DAA₁ равны по 60⁰ каждый. Найдите угол между прямой BA₁ и плоскостью BDВ₁.

15) Две окружности касаются друг друга внутренним образом, причем два радиуса большей окружности касаются меньшей окружности и образуют угол, равный . Тогда отношение радиуса большей окружности к радиусу меньшей равно

16) Если высота ромба, проведенная из вершины тупого угла, делит противолежащую сторону пополам, то тупой угол ромба ( в градусах) равен

17) Около правильной четырехугольной призмы описан ци­линдр. Объем цилиндра равен 24 π. Найдите радиус ци­линдра, если диагональ боковой грани призмы равна 5.

18) В правильную четырехугольную призму вписан ци­линдр. Объем цилиндра равен 16π√2, а радиус окруж­ности, описанной вокруг основания призмы равен 2√2 . Найдите диагональ призмы.

19) В треугольной пирамиде три ребра, выходящие из одной вершины, взаимно перпендикулярны и равны 1, и 2 см. Найти объем пирамиды.

20) В треугольнике PQR сторона PR равна 3, сторона PQ равна 4, а угол при вершине Q равен . Если расстояние от вершины Q до прямой PR меньше, чем , то площадь треугольника равна (ответ округлить до ближайшего целого числа с избытком )

21) В прямоугольном треугольнике АВС расположен прямоугольник ADKM так, что его сторона AD лежит на катете АВ, сторона АМ − на катете АС, а вершина К − на гипотенузе ВС. Катет АВ равен 5, а катет АС равен 12. Если площадь ADKM равна 40/3, а диагональ меньше 8, то сторона прямоугольника равна

22) Около правильной треугольной призмы описан цилиндр. Площадь боковой поверхности цилиндра равна 16π. Най­дите объем призмы, если сторона ее основания равна 5.

23) В правильную шестиугольную призму вписан цилиндр. Найдите высоту призмы, если ее площадь равна 54√3,а радиус цилиндра равен 3.

24) В правильной четырехугольной пирамиде сторона основания равна 6дм, а высота 4 дм. Найти боковую поверхность усеченной пирамиды, отсекаемой от данной плоскостью, параллельной основанию пирамиды и отстоящей от него на 1дм.

25) К окружности, вписанной в квадрат со стороной, равной 7, проведена касательная, пересекающая две его стороны. Тогда периметр отсеченного треугольника равен

26) Около трапеции ABCD с основанием AD и ВС описана окружность радиусом 5. Центр описанной окружности лежит на основании AD. Если

Основание ВС равно 6, тогда диагональ АС равна

27) Прямой круговой цилиндр пересечен плоскостью так, что в сечении получился квадрат. Найдите площадь бо­ковой поверхности цилиндра, если известно, что радиус основания равен 10 см, а расстояние от сечения до оси цилиндра 6 см.

28) Прямой круговой конус пересечен плоскостью парал­лельной основанию на расстоянии 3 см от вершины. Найдите объем конуса, если известно, что радиус сече­ния равен 4 см, а образующая конуса равна 10 см.

29) В основании прямого параллелепипеда лежит параллелограмм со сторонами 1 и 4 см и острым углом . Большая диагональ параллелепипеда

равна 5 см. Определить его объем.

30) Основание пирамиды служит ромб с острым углом . Боковые грани наклонены к плоскости основания под углом в . Определить полную поверхность пирамиды, если радиус вписанного в ромб круга равен .