
- •Математика Пособие для подготовки к егэ в 2 частях
- •Часть 2
- •11 Кафедра теоретической гидрометеорологии вунц ввс "вва";
- •Введение
- •Свойства логарифмов
- •1.3. Тождественные преобразования показательных и логарифмических выражений
- •Задачи для самостоятельного решения
- •1.4. Показательные уравнения
- •Задачи для самостоятельного решения
- •1.5. Показательные неравенства
- •Задачи для самостоятельного решения
- •1.6. Логарифмические уравнения
- •Задачи для самостоятельного решения
- •1.7. Логарифмические неравенства
- •Задачи для самостоятельного решения
- •1.8. Системы показательных и логарифмических уравнений и неравенств
- •Задачи для самостоятельного решения
- •2. Задачи с параметрами
- •Задачи для самостоятельного решения
- •3. Геометрия
- •3.1. Основные формулы
- •Радианное и градусное измерение углов
- •Заключение
- •Библиографический список
- •Оглавление
- •Математика
- •Часть 2
- •3 94006, Воронеж, ул. 20-летия Октября, 84
Министерство образования и науки РФ
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Воронежский государственный архитектурно-строительный университет»
Математика Пособие для подготовки к егэ в 2 частях
Часть 2
Составители:
М.Ю. Глазкова, Н.Н. Некрасова
В оронеж
2014
оронеж
2014
УДК 372.8.51
ББК 74.262.21
М34
Рецензенты:
11 Кафедра теоретической гидрометеорологии вунц ввс "вва";
С.А. Шабров, к.ф.-м.н., доц.кафедры математического анализа Воронежского государственного университета
М34
|
Математика. Пособие для подготовки к ЕГЭ: учеб. пособие : в 2 ч. / сост. М.Ю. Глазкова, Н.Н. Некрасова; Воронежский ГАСУ. Ч. 2. Воронеж, 2013. 78 с.
ISBN 978-5-89040- 000-0 |
Пособие разработано для выпускников средних школ и абитуриентов как вспомогательный материал для подготовки к единому государственному экзамену. К каждому рассматриваемому разделу приводится необходимый теоретический материал, разобраны решения типовых задач и даны задачи для самоконтроля.
Пособие может быть использовано учителями для подготовки учащихся к экзамену по математике в форме ЕГЭ, а также старшеклассниками и абитуриентами для самоподготовки и самоконтроля.
Ил. 34. Библиогр.: 9 назв.
УДК 372.8.51
ББК 74.262.21
Печатается по решению
научно-методического совета Воронежского ГАСУ
ISBN 978-5-89040- 518-0 (ч. 2) |
© Глазкова М.Ю., Некрасова Н.Н, составление,2014 |
ISBN 978-5-89040-443-5 |
© Воронежский ГАСУ, 2014 |
Введение
Вторая часть пособия включает в себя следующие разделы: преобразования логарифмических и показательных выражений, логарифмические и показательные уравнения и неравенства, системы логарифмических и показательных уравнений и неравенств, геометрия и задачи с параметрами.
К каждому разделу приводятся необходимые теоретические материалы.
Рассматриваются как решения типичных примеров, так и нестандартные задачи ( задачи геометрические задачи группы С и задачи с параметрами − С5). В конце каждого раздела даются задачи для самостоятельного решения.
Однако пособие не является ни учебником, ни справочником, ни сборником задач по математике в традиционном понимании. Эта книга предназначена главным образом для самостоятельного контроля процесса подготовки к ЕГЭ. Если Вы настроитесь на серьезную и кропотливую работу, если будете стараться выполнять все предложенные задания, то успех не заставит себя ждать.
Решенные
в пособии примеры надо разбирать
аккуратно, "с карандашом в руках",
по мере необходимости восстанавливая
пропущенные выкладки. Решение многих
задач сознательно приведено в кратком
виде, и разбор этих решений
![]() важный элемент самостоятельной
подготовки.
важный элемент самостоятельной
подготовки.
Кроме разбора решённых задач, Вам необходимо постараться выполнить как можно больше приведенных задач для самостоятельного решения.
Удачи Вам на экзамене. Помните: удача сопутствует упорным!
1. ЛОГАРИФМИЧЕСКАЯ И ПОКАЗАТЕЛЬНАЯ ФУНКЦИИ. ЛОГАРИФМИЧЕСКИЕ И ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ
И НЕРАВЕНСТВА
1.1. Показательная функция
![]()
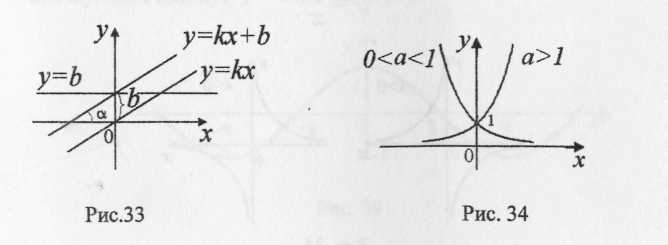
Рис. 1
1.
Область определения функции
множество
![]() всех
действительных чисел.
всех
действительных чисел.
2.
Область значений функции
множество
всех
положительных действительных чисел:
![]() .
.
3.
При
![]() функция возрастает, т.е. если
функция возрастает, т.е. если
![]() то
то
![]() При
При
![]() функция убывает, т.е. если
то
функция убывает, т.е. если
то
![]()
4.
Если
![]() то
то
![]()
5.
Производная функции:
![]()
Свойства
степеней
![]()
1.
![]() . 2º.
. 2º.
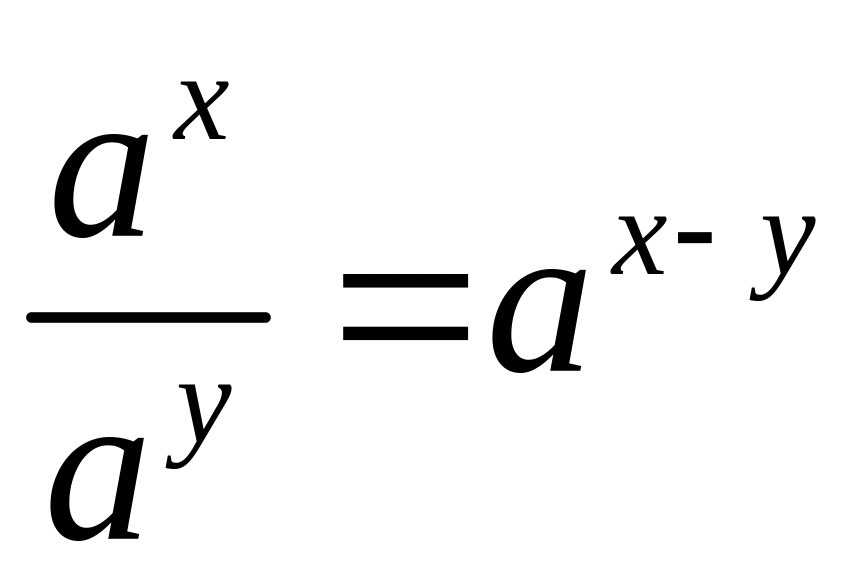 . 3.
. 3.
![]() . 4.
. 4.
![]() .
.
5.
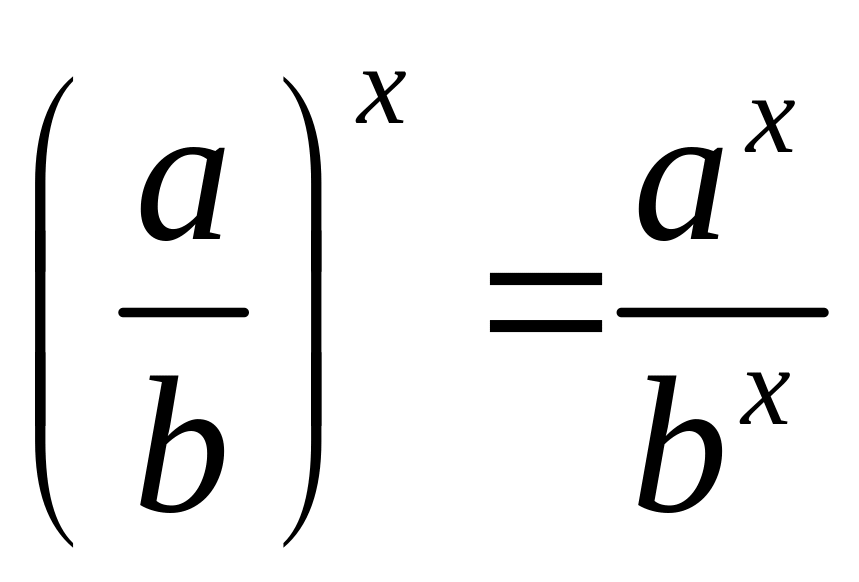 . 6º.
. 6º.
![]() . 7.
. 7.
![]() . 8.
. 8.
![]() .
.
1.2. Логарифмическая функция
![]()
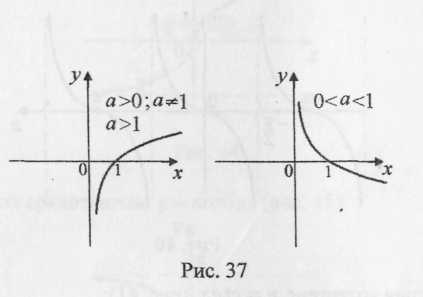
Рис. 2
1.
Область определения функции
множество
![]() всех
положительных действительных чисел.
всех
положительных действительных чисел.
2. Область значений функции множество всех действительных чисел.
3.
При
функция возрастает, т.е. если
![]() , то
, то
![]() При
функция убывает, т.е. если
то
При
функция убывает, т.е. если
то
![]()
4.
Если
![]() то
то
![]()
5.
Производная функции:
![]()
Преобразование показательных и логарифмических выражений основаны на применении основных свойств соответствующих функций, показателя степени и свойств логарифмов.
Логарифмом
числа
![]() по основанию
по основанию
![]()
![]()
называется
показатель степени
![]() ,
в которую надо возвести число
,
чтобы получить число
:
,
в которую надо возвести число
,
чтобы получить число
:
![]() откуда
откуда
![]()
Заметим,
что каждая из функций
![]() является обратной по отношению к другой.
является обратной по отношению к другой.
