1.5 . Дифференциальные уравнения второго порядка, допускающие понижения порядка
В данном пункте рассматриваются некоторые наиболее важные типы уравнений второго порядка, допускающие понижение порядка, вида [I, гл. XIII, §18, §2, §14].
Наиболее простым является тот случай, когда правая часть уравнения зависит только от х
.
(1.14)
Общее решение в этом случае получаем с помощью последовательного интегрирования
,
;
,
,
.
Решение задачи
Коши с начальными условиями
,
может быть записано в виде
.
На практике обычно не пользуются готовыми формулами, а, используя начальные условия, находят значения постоянных постепенно, в процессе интегрирования.
Пример.
Решить уравнение
.
Решение.
Умножая обе части на
и интегрируя, получим
,
;
,
.
Пример.
Найти решение уравнения
,
удовлетворяющее условиям
,
,
.
Решение.
Перепишем уравнение в виде
.
Отсюда получим
,
.
Подставим начальное
условие
и найдем постоянную
,
.
Следовательно,
.
Умножая обе части уравнения на
и интегрируя, получим
,
.
Используя начальное
условие
,
получим
,
.
Получим частное решение, удовлетворяющее
начальным данным:
.
Рассмотрим ОДУ вида
, (1.15)
не содержащее
искомую функцию у. Подстановка
приводит уравнение (1.15) к уравнению
первого порядка относительно функции
:
.
Решая это уравнение,
находим функцию
,
а затем и
.
Пример.
Решить уравнение
.
Решение.
Вводим новую функцию
,
тогда
.
Подставив ее в уравнение, имеем
.
Это линейное
уравнение первого порядка относительно
и его решение разыскиваем в виде
произведения
Учитывая требования
(см. 1.3)
,
,
находим функцию
:
подставляем в уравнение для определения
Отсюда
.
Таким образом,
,
и можно найти функцию y
,
Еще один тип уравнений, допускающий понижение порядка, следующий
.
(1.16)
Это уравнение, не содержащее явно независимую переменную x.
Для его решения
положим
Тогда по правилу дифференцирования
сложной функции, получим
;
Подставляя
и
в уравнение (1.16), получим уравнение
первого порядка для вспомогательной
функции
Решая его, найдем
как функцию у и постоянной
:
,
а затем найдем и
из соотношения
Пример. Найти решение задачи Коши:
Решение.
Это уравнение не содержит х и,
следовательно, относится к типу (1.16).
Делая замену
и подставляя в уравнение, получим
.
Подставляя начальные
данные
найдем
.
Поскольку
,
то
.
Имеем
,
Подставляя
,
получим
,
после чего найдем у
Задачи для самостоятельного решения.
.
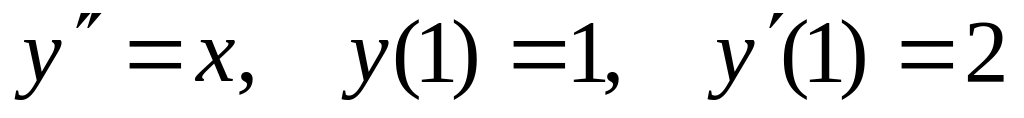Ответ:
.
2.
.
Ответ:
.
3.
. Ответ:
.
2. Линейные дифференциальные уравнения
Линейным дифференциальным уравнением - го порядка называется уравнение вида
, (2.1)
где функции
,
непрерывны на интервале
.
Если функция
на
,
то уравнение (2.1) называется линейным
неоднородным уравнением. Если
на
,
уравнение называется линейным однородным.
Общее решение
линейного однородного уравнения
-го
порядка имеет вид
где
- произвольные постоянные;
- его частные
линейно независимые решения.
Напомним, что
функции
называются линейно зависимыми на
интервале
,
если существуют такие постоянные
,
что
(2.2)
при всех
,
причем
.
Если же равенство (2.2) имеет место лишь
при
,
то функции
называются линейно независимыми.
Общее решение неоднородного уравнения представляет собой сумму частного решения линейного неоднородного уравнения и общего решения соответствующего однородного уравнения.
,
где
- общее решение неоднородного уравнения;
- его частное
решение;
- общее решение соответствующего однородного уравнения.
Частные линейно
независимые решения линейного однородного
уравнения с постоянными коэффициентами
определяются по корням характеристического
уравнения
Рассмотрим уравнение второго порядка с постоянными коэффициентами:
.
Его характеристическое
уравнение
может иметь:
1) два различных
действительных корня
;
2) действительный кратный корень кратности двух
;
3) два комплексно
сопряженных корня
В зависимости от
вида корней, в первом случае частными
решениями однородного уравнения будут
функции
и
,
а общее решение запишется в виде
Во втором случае
(действительный корень кратности двух)
частными линейно независимыми решениями
будут функции
,
,
а общее решение запишется как
В случае комплексных
корней
:
Пример 1. Найти общее решение уравнения
Решение.
Характеристическое уравнение
имеет два различных корня:
,
и общее решение уравнения
запишется как
.
Пример 2. Найти общее решение уравнения
Решение.
Характеристическое уравнение
запишем в виде
.
Отсюда следует, что оно имеет один
единственный корень кратности двух:
,
и общее решение уравнения
запишется как
.
Пример 3. Найти общее решение уравнения
Решение.
Решая характеристическое уравнение
,
находим его корни
,
.
Корни комплексно сопряженные, причем
.
Следовательно, общее решение имеет
вид
Если в уравнении (2.1) с постоянными коэффициентами функция имеет вид
то это уравнение
называется неоднородным со специальной
правой частью. Здесь
и
– многочлены порядка
и
соответственно. Частное решение
неоднородного уравнения ищется точно
в таком же виде
(2.3)
где функции
и
-
многочлены с неопределенными коэффициентами
порядка
.
Кроме того, показатель степени r
в (2.3) – это число корней характеристического
уравнения равных
.
Пример. Определить вид частного решения, если
.
Решение.
Так как
получим, что
и
Показатель степени
r – число корней
характеристического уравнения равных
3 (так как
).
Например, для уравнения из примера 3
,
так как его характеристическое
уравнение не имеет корней, равных 3. Для
уравнения из примера 2 число
,
так как его характеристическое уравнение
имеет корень, равный 3 кратности два (то
есть встречается среди корней
характеристического уравнения дважды).
Пример. Определить вид частного решения неоднородного уравнения, если
Решение.
Так как
,
то частное решение имеет вид
Показатель степени
r – число корней
характеристического уравнения,
соответствующего однородного уравнения,
равных
.
В частности, если
-
правая часть уравнения из примера 3, то
,
так как корни равны
.
Если же
-
правая часть уравнения из примеров
1 и 2, то
.
Другой способ решения неоднородного линейного уравнения - метод вариации произвольных постоянных, применим для любых правых частей и состоит в следующем.
1. Находим общее решение соответствующего однородного уравнения
предполагая, что
функции
,
- функции от х.
Для их определения составляем систему уравнений
(2.4)
2. Решаем систему
уравнений (2.4) относительно
,
.
Относительно
и
эта система уравнений является линейной
алгебраической и может быть решена по
формулам Крамера:
;
(2.5)
где
,
и
определители системы.
3. Интегрируем
решение системы уравнений (2.5) по х
и определяем функции
и
:
Окончательно, решение неоднородного уравнения можно записать в виде
.
Пример.
Найти общее решение неоднородного
уравнения
Решение. Решим соответствующее однородное уравнение
Характеристическое
уравнение
имеет корни
Следовательно, общее решение однородного
уравнения запишем в виде
Составим систему уравнений:
(2.6)
Решаем систему
уравнений (2.6) относительно
и
по формулам Крамера:
Интегрированием
находим функции
и
:
;
( 2.7)
При вычислении
интеграла в (2.7) использована подстановка
.
В итоге общее решение уравнения имеет
вид
Рассмотрим некоторые задачи.
Задача 1. Найти общее решение неоднородного уравнения
.
(2.8)
Решение. Рассмотрим однородное уравнение
.
Его характеристическое
уравнение
имеет корни
и общее решение однородного уравнения
запишется в виде
Так как
,
частное решение неоднородного уравнения
ищем в виде
.
(2.9)
(
,
поскольку характеристическое уравнение
не имеет корней равных
).
Для определения коэффициентов
решение (2.9) подставим в исходное
уравнение(2.8):
Равенство (2.10) можно преобразовать к виду
Так как требуется,
чтобы функция
была решением уравнения, то равенство
(2.10) должно выполняться тождественно.
Следовательно, коэффициенты при
одинаковых функциях в левой и правой
частях (2.10) должны быть равны:
(2.11)
Решая систему
уравнений (2.11), определим коэффициенты
:
.
Следовательно, частное решение
неоднородного уравнения и общее решение
неоднородного уравнения будут иметь
вид:
Задача 2. Найти частное решение неоднородного уравнения
,
удовлетворяющее начальным условиям
(2.12)
Решение.
Характеристическое уравнение
соответствующего однородного уравнения
имеет корни
и общее решение однородного уравнения
имеет вид
Частное решение неоднородного уравнения ищем в форме
(2.13)
(
,
так как характеристическое уравнение
имеет корень, равный
).
Коэффициенты
определим, подставляя решение (2.13) в
исходное уравнение
(2.14)
Приравнивая
коэффициенты при одинаковых функциях
в левой и правой частях тождества (2.14),
получим систему уравнений для определения
:
.
Решая ее, найдем
:
и общее решение неоднородного уравнения
будет иметь вид:
Чтобы определить частное решение, удовлетворяющее начальным условиям (решить задачу Коши), найдем производную общего решения неоднородного уравнения
Подставляя найденное
решение и его производную в начальные
условия (2.12), получим систему уравнений
для определения коэффициентов
:
Решая ее, определим
:
.
Следовательно, искомое частное решение запишется в виде
.
Примеры для самостоятельного решения.
Пример 1. Найти общее решение неоднородного уравнения
Ответ:
Пример 2. Найти общее решение неоднородного уравнения
Ответ:
Пример 3. Методом вариации произвольной постоянной найти общее решение неоднородного уравнения
Ответ:
Пример 4. Решить задачу Коши:
Ответ:
