1.3 . Линейные дифференциальные уравнения первого порядка

Так называются уравнения вида

, (1.7)

где , – непрерывные функции от х в той области, в которой разыскивается решение этого уравнения. Это уравнение линейно как относительно функции у, так и относительно ее производной. [I, гл.XIII, §7] или [2, §13].

Если , то уравнение (1.7) называется линейным однородным. Само уравнение (1.7) называют линейным неоднородным.

Ясно, что линейное однородное уравнение является уравнением с разделяющимися переменными. Решение уравнений такого типа описано в 1.1. Решение уравнения (1.7) можно получить, разыскивая его в виде , где одна из функций u или v является частным решением соответствующего уравнения:

, , .

Тогда для функции получим уравнение . Откуда

, ;

.

Решение уравнения (1.7) с начальными условиями дается выражением

.

Пример. Решить уравнение .

Решение. Ищем его в виде . Дифференцируя по х, имеем

.

Подставим эти выражения в уравнение

(1.8)

и потребуем, чтобы функция удовлетворяла однородному уравнению .

Отсюда , , .

Подставим функцию v в уравнение (1.8) и учитывая равенство нулю подчеркнутой части, получим уравнение для

.

Отсюда , и, таким образом,

.

Задачи для самостоятельного решения

1. . Ответ: .

2. , . Ответ: .

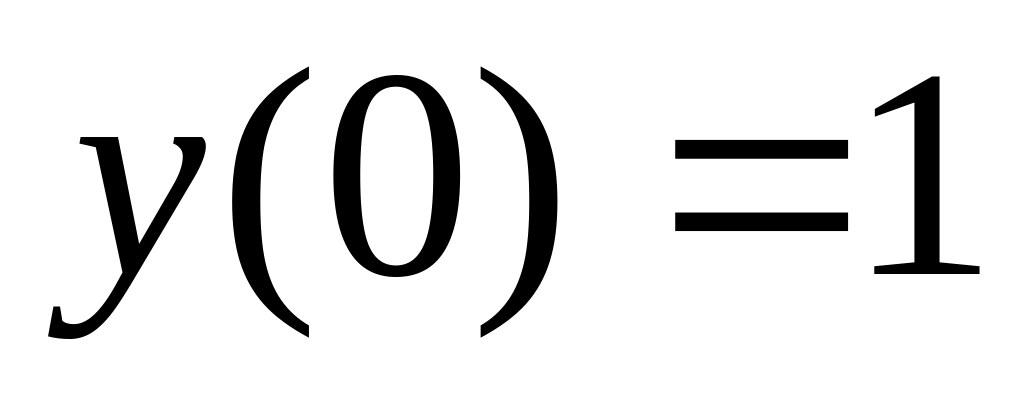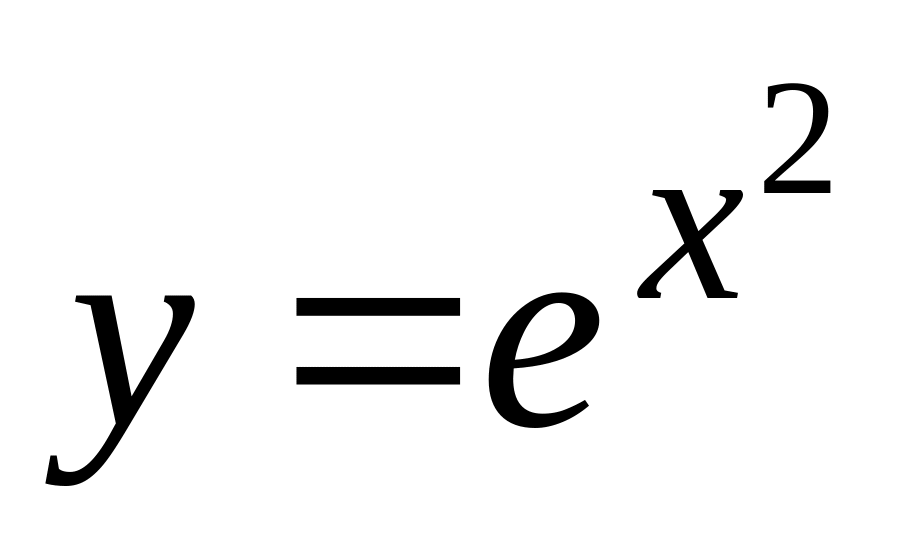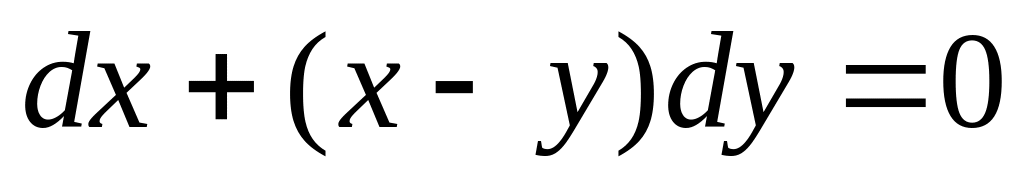3. . Ответ: .

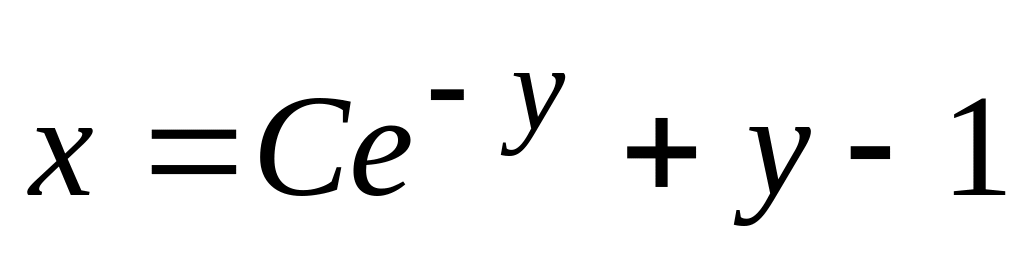Указание. Уравнение линейно относительно х и .

1.4. Некоторые применения дифференциальных уравнений первого порядка

К дифференциальным уравнениям первого порядка приводят различные физические задачи. Основную трудность при их решении представляет составление дифференциальных уравнений. Здесь не существует универсального метода. Каждая задача требует индивидуального подхода, Основанного на понимании законов физики, и умения переводить физические задачи на математический язык. Рассмотрим несколько таких задач.

З а д а ч а о р а д и о а к т и в н о м р а с п а д е. Экспери­ментальным путем установлено, что скорость распада радиоактив­ного вещества, т. е. скорость изменения его массы в зависимости от времени, прямо пропорциональна его количеству. Установим закон изменения массы т радиоактивного вещества в зависимости от времени t, считая, что начальная масса вещества при t = 0 была .

Пусть в момент времени t масса вещества есть т, в момент вре­мени масса составляет . За время распадается масса . Отношение  средняя скорость распада за время , a мгновенная скорость распада в момент времени t.

Согласно условию

(1.9)

где k  коэффициент пропорциональности (знак минус взят по­тому, что масса вещества убывает с течением времени, а производ­ная убывающей функции отрицательна). Получено дифференциаль­ное уравнение первого порядка, из которого надо найти зависи­мость массы от времени t. Решая уравнение, находим откуда

. (1.10)

Формула (1.10) дает зависимость массы вещества как функции времени. В данной задаче постоянная С имеет определенное значе­ние, а именно: при получаем Подставляя это значение С в формулу (1.10), получаем искомую зависимость массы радиоактивного вещества от времени:

(1.11)

Равенство (1.10) представляет собой общее решение дифферен­циального уравнения, а равенство (1.11)  частное решение, отве­чающее начальному условию данной задачи.

Коэффициент k определяется экспериментально. Например, для радия . Промежуток времени Т, за который распада­ется половина первоначальной массы радиоактивного вещества, называют периодом полураспада этого вещества. Подставляя в фор­мулу (1.11) вместо m значение , вместо k  значение 0,000447, получаем уравнение для определения периода полураспада Т радия:

откуда лет.

З а д а ч а о з а к о н е «е с т е с т в е н н о г о р о с т а». За­кон «естественного роста»  это закон, согласно которому скорость «роста» вещества прямо пропорциональна его количеству. Найдем формулу для определения изменения количества вещества у в зави­симости от времени t, считая, что в начальный момент коли­чество вещества было равно .

Здесь независимой переменной является время t, а искомой ве­личиной  количество вещества в любой момент времени. Скорость «роста» вещества есть скорость изменения величины у в зависимос­ти от переменной t. Используя, как и в предыдущей задаче, физический смысл про­изводной, можно записать закон «естественного роста» следующим образом:

(1.12)

где k > 0  коэффициент пропорциональности. Уравнение (1.12), отличающееся только знаком правой части от уравнения (1.9), опи­сывает многие процессы «размножения».

Решение уравнения (1.12), удовлетворяющее заданному началь­ному условию , , имеет вид

(1.13)

Формула (1.13) и выражает закон «естественного роста». Согласно этому закону, например, происходит «размножение» нейтронов в ядерных реакциях, размножение бактерий, рост кристаллов и т. п.