8. Элементарные функции комплексной переменной (кп)

Элементарные функции КП, изучаемые в данном курсе, явля­ются естественным распространением в комплексную область основ­ных элементарных функций действительной переменной x. Однако при таком распространении функции приобретают подчас новые свойства: показательная функция КП оказывается периодической, функции sinx и cosx перестают быть ограниченными по мо­дулю и т.д.

Теория элементарных функций КП была в основном создана Л. Эйлером в его работах сороковых годов ХVIII в. Эти работы намного опережали эпоху. Например, теория логарифма была признана с большим трудом и далеко не сразу.

Дробно-линейная функция.

Дробно - линейной функцией называется функция вида

(8)

где a, b, c, d - некоторые комплексные числа. Считаем, что а и с одновременно в нуль не обращаются.

Рассмотрим последовательность отображений, осуществляемых функцией (8). Числитель выражения (8) есть линейная функция

. (9)

Отображение W₁(z) - конформно, так как W₁^’=а 0. Отображение осуществляет параллельный перенос всех точек плоскости z на вектор (это следует из геометрического смысла операции сложения комплексных чисел).

Рассмотрим выражение :

, (10)

. (11)

Следовательно, в общем случае линейная функция следующим образом преобразует векторы плоскости z: а) концы всех векторов смещаются на вектор ; б) полученные векторы растягиваются в раз и поворачиваются на угол .

Рассмотрим функцию .

Точки А и B (рисунок 2) называются симметричными относительно окружности радиуса R, если А и B лежат на одном луче, проведенном из центра окружности; произведение их расстояний от центра окружности равно квадрату радиуса окружности:

. (12)

Из (12) следует, что , т.е. точкой, симметричной центру окружности, является .

Покажем, что если центр окруж­ности находится в точке z=0, то симметричной для точки будет точка .

Проверим выполнение условий симметричности:

Рисунок 2

.

Отсюда следует, что точки и симметричны относи­тельно окружности радиуса . В свою очередь точки и симметричны относительно оси ОХ плоскости как взаимно-сопряженные.

Поэтому отображение состоит из двух симметричных преобразований (рисунок 3).

Функция осуществляет взаимно однозначное отображение полной плоскости z на плоскость W₂ причем , ; при этом внутренность круга единичного радиуса переходит в его внешность на плоскости W₂ , окружность единичного радиуса переходит в такую же окружность (рисунок 3).

Рисунок 3.

Докажите, что сказанное выше верно только для круга единичного радиуса .

В точках производная определена так: , т.е. осуществляет конформное отображение.

3. Рассмотрим общее дробно-линейное преобразование

считая ФКП осуществляет взаимно-однозначное отображение , так как , .

Нетрудно видеть, что общее дробно-линейное отображение можно получить, последовательно осуществляя линейные отображения и отображение :

. (13)

Из (13) получаем последовательность отображений:

1) ;

2) ;

3) , т.е. два линейных отображения и одно типа .

Следовательно, если какое-либо свойство присуще линейному и отображению, то это же свойство будет характерным и для дробно-линейного отображения.

Докажем, что дробно-линейное отображение обладает круговым свойством: окружности, принадлежащие плоскости преобразу­ются в окружности, принадлежащие плоскости W . При этом прямые считаем окружностями бесконечно большого радиуса.

Убедимся в том, что отображение обладает круговым свойством:

, , ,

.

Уравнение семейства окружностей на z записывается в виде

Уравнение образа этого семейства на плоскости W

.

Рассмотрим на плоскости точку . При отображении . Следовательно, образ каждой прямой или окружности, проходящей в плоскости через точку , содержит точку , т.е. все прямые и окружности, проходящие в плоскости через точку , переходят в прямые на плоскости W. Все прямые и окружности, не проходящие через , в плоскости W являются окружностями, так как ни одна точка их прообразов не перейдет в точку .

Пример 2. Отобразить конформно верхнюю полуплоскость на внутренность круга так, чтобы граница полуплоскости перешла в окружность . Дробно-линейное отображение обладает круговым свойством, поэтому для решения поставленной задачи достаточно так подобрать коэффициенты функции , чтобы установить соответствие между выбранными точками оси ( ) и наперед заданными точками окружности . Пусть , тогда

,

т.е. для задания дробно-линейного отображения достаточно знать три параметра для чего необходимо задать соответствие .

Рисунок 4.

Например, так подберем чтобы

Из (12) имеем (k = 1, 2, 3). Отсюда для нахождения получим систему трех линейных уравнений:

Отсюда , , .

Таким образом .

Степенная функция

Изучим некоторые свойства отображения, осуществляемого функцией .

Представим числа z и W в тригонометрической форме:

(14)

По формуле Муавра

(15)

Отсюда видно, что при отображении с помощью степенной функции происходит поворот каждого вектора на угол и растяжение в раз. Легко проверяется следующее утверждение: если две точки z₁ и плоскости z таковы, что , то их образы и равны.

Поэтому для выделения областей плоскости Z, для точек которых степенная функция осуществляет взаимно однозначное отображение, необходимо потребовать, чтобы область не содержала точек с аргументами, отличающимися на целое кратное .

Т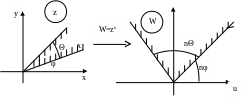 акими областями на плоскости являются углы (рисунок 5)

Рисунок 5.

(к=0, I, ...) (16)

Области, для точек которых данная функция осуществляет взаимно однозначное отображение, называются областями однолистности данного отображения (функции).

Следовательно, области являются областями однолистности отображения, задаваемого степенной функцией ..

На примере отображения посредством функции введем одно важное понятие. Из предыдущего следует, что областями однолистности для данной функции на плоскости являются полуплоскости . Очевидно, что левая и правая полуоси ОХ как стороны угла переходят в лучи и на плоскости W , т.е. в полуось. ReW=0.

Чтобы для всех точек полуплоскости сохранить условие однолистности отображения, мысленно разрежем плоскость W по полуоси и слегка сместим края разреза (в плоскости W).

Получим геометрическое представление о плоскости с разрезом по оси 0u.

Пользуясь этим примером, можно объяснить происхождение термина однолистность: для отображения точек верхней полуплоскости потребовалась целая плоскость w (один лист); для отобра­жения всех точек плоскости z потребуется еще одна плоскость (лист).

Будем говорить, что луч переходит в верхний берег разреза, луч - в нижний берег разреза.

Вообще, если , то каждый из углов плоскости z отображается в плоскость с разрезом, а вся плоскость z отображается в n-листную плоскость w.

Отметим, что изучаемое отображение (n - целое положительное) конформно всюду, кроме точки :

. (17)

Используя методы анализа, можно вывести аналогичную (17) формулу

для любого действительного показателя r: ,

(17’)

Функция, обратная к , называется корнем n-й степени и записывается в виде . Число W называется корнем n-й степени из числа z, если .

В алгебре комплексных чисел было выяснено, что корень n-й степени из числа z имеет n различных значений.

Следовательно, функция n-значная: . Значение определяется значением аргумента, выбранным для точки z (вспомним, что значение аргумента числа z определяется с точностью до ).

Обозначим через одно из значений аргумента точки и предположим, что точка описывает замкнутую кривую С на плоскости Z так, что начало координат остается вне области D, границей которой является С (рисунок 6). Через обозначим значения аргументов точек .

Очевидно, при обходе контура C меняется непрерывно от и при полном обходе контура C принимает прежнее значение, равное .

Рисунок 6.

Следовательно, в плоскости W точка

,

описывая замкнутую кривую ,начиная от точки

,

вернется к своему прежнему значению .

Значения корня, определяемые другим выбором аргумента /например, (к = I, 2,...)/ при полном обходе по кривой С также описывают замкнутые кривые , отличающиеся от C лишь поворотом на .

Теперь рассмотрим кривую , внутренность которой содержит точку z=0 ( рисунок 6, пунктир).

При полном обходе кривой L от точки со значением аргумента соответствующая точка не возвращается в положение , а занимает новое положение,

так как аргумент точки при полном обходе по L получил приращение своему начальному значению , точка вернется лишь при n-кратном обходе кривой L , поскольку в этом случае аргумент точки , получит приращение . На рисунке 7 показан случай n=3.

Отсюда следует, что в любой области , не содержащей ни одной кривой, обходящей точку , можно выделить n непрерывных и однозначных функций, принимающих одно из значений корня .

Эти n функций называются ветвями многозначной функции ; их значения для каждого фиксированного z отличаются друг от друга множителями

.

В этом случае каждая из ветвей является непрерывной функцией и осуществляет однолистное (взаимно однозначное) отображение области D. Поэтому каждой точке области D применима теорема о производной обратной функции

Если область в плоскости z содержит хотя бы одну кривую, об­ходящую точку , то ветви отделить нельзя, они непрерывно переходят одна в другую.

Показательная функция и логарифм

Показательная функция определяется для любого комплексного соотношением

(18)

Из этого определения вытекают следующие свойства :

1. Для действительных чисел получаем показательную функцию действительного переменного .

2. Функция всюду аналитична и ее производная вычис­ляется по формуле

.

Выполнение условий Даламбера-Эйлера проверяется элементарно. Используя факт независимости производной от направления, по которому происходит стремление текущей точки к предельной, возьмем производную по направлению, параллельному оси Оx:

.

3. Сохраняется основное свойство показательной функции (в области действительного переменного), выражаемое теоремой сложения

4. Показательная функция не обращается в нуль ни при каких значениях показателя, так как

.

Полагая в (18) х=0, , получим формулу Эйлера:

(19)

С помощью формулы Эйлера любое комплексное число можно записать в показательной форме

(20)

5. Показательная функция является периодической с периодом , так как . В силу свойства периодичности изучение функции сводится к изучению ее свойств в полосе шириной и параллельной оси Оx, например в полосе /вообще говоря, в одной из полос /. Действительно, силу периодичности. Отсюда, .

Значит отображение, определяемое функцией , однолистно в указанных полосах.

В ведем в плоскости W полярные координаты . Тогда по формуле Эйлера. Из (18) .

Рисунок 7.

Отсюда следует, что прямые , (в плоскости z ) отображаются в окружности радиуса и лучи соответственно (рисунок 7).

При этом ось Оx ( ) и прямая преобразуются в лучи и . Чтобы соблюсти взаимную однозначность отображения, на плоскости w производим разрез по полуоси и . Тогда Оx переходит в верхний берег разреза, а - в нижний берег.

Таким образом, функция отображает каждую горизонтальную полосу плоскости z шириной на плоскость с разрезом по полуоси . Вся плоскость Z при этом отображается в бесконечнолистную плоскость w .

Логарифмическая функция определяется как функция, обратная к показательной; число W называется логарифмом числа z, если и обозначается .

Из определения логарифмической функции и свойств показательной функции получим основные свойства логарифмов от комплексных чисел.

I. Пусть

(21)

Формула (21) - есть обобщение известного из элементарной математики свойства логарифма.

2. Пусть . Тогда по формуле (21)

В этой формуле, так как - действительное положительное число, в первом слагаемом использовано обычное обозначение натурального логарифма.

Как известно - бесконечнозначная функция, поэтому любое комплексное число имеет бесконечное множество значений логарифма:

(22)

В этой формуле - главное значение аргумента комплексного числа.

Условимся через обозначать главное значение бесконечнозначной функции соответствующее : ,

Рисунок 8

Значение зависит от того, какое значение выбрано для аргумента комплексного числа.

Рассмотрим в плоскости Z две кривые C и L, рисунок 8. Пусть точка пробегает кривую С от начального положения . Выберем для значений аргументов точек главные их значения. При возвращении в точку z₀ значение аргумента, которое менялось от точки к точке при прохождении кривой С, останется прежним - .

Соответствующая точка в плоскости w также опишет замкнутую кривую Ć и вернется в прежнюю точку .

При выборе в качестве аргументов z значений точки в плоскости W будут описывать кривые , которые получаются из смещением на по оси . Таких кривых будет бесконечно много. Они дадут бесконечно много отделенных друг от друга ветвей функции .

Если кривая L в, плоскости Z содержит внутри своего контура точку , то при каждом обходе по замкнутому контуру L аргументы соответствующих точек z возрастают на , поскольку радиус-вектор поворачивается на угол при возвращении в точку z. Следовательно, соответствующая точка будет описывать незамкнутую кривую , ибо у функции

мнимая часть изменится на при каждом возвращении точки z в прежнее положение .

В этом случае говорят, что ветви функции отделить нельзя: они непрерывно переходят одна в другую. Таким образом, если область не содержит кривых, обходящих начало координат , ветви отделяются и каждая из них осуществляет взаимно-однозначное отображение области D.

Следовательно, по теореме о производной обратной функции

(23)

Тригонометрические и гиперболические функции

По формуле Эйлера (19) имеем

(24)

Формулы (24) дают выражение тригонометрических функций действительного переменного через показательную функцию.

Примем по определению для любого комплексного числа z

(25)

Определенные функции и являются линейными комбинациями показательных функций переменного , поэтому свойства тригонометрических функций, в основном, обусловлены свойствами показательной функции.

1. Для действительных и совпадают с соответствующими функциями и .

2. sinz и cosz всюду аналитичны, так как всюду аналитична показательная функция.

3. sinz и подчиняются обычным (из анализа действительной переменной) формулам дифференцирования:

(26)

4. и периодичны с периодом . Вследствие периодичности показательной функции

Аналогично .

С помощью несложных выкладок можно убедиться, что выполняются обычные тригонометрические тождества

и т.д.

Поскольку периодом функций и является действительное число , областями однолистности соответствующих отображений будут вертикальные полосы

, так как, например,

Тригонометрические функции в комплексной плоскости обладают новым, по сравнению с теми же функциями действительного переменного, свойством: их модули бесконечно возрастают при стремлении вдоль оси Оy, т.е. при .

Действительно

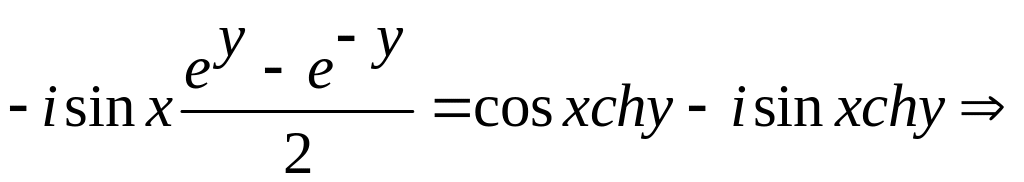
Отсюда видно, что является периодической по x функцией (при фиксированном y ) и .

Гиперболические функции комплексного переменного и

определяются по аналогии с соответствующими функциями действительного переменного:

(27)

Эти функции в силу определения выражаются через тригонометри­ческие по формулам

(28)

Гиперболические функции вместе с показательной являются периодическими, , и всюду аналитическими:

.

Функции тангенса и котангенса определяются обычными формулами:

.