7. Гармонические функции

Гармонической в области D функцией называется действительная функция двух действительных переменных, обладающая в этой области непрерывными вторыми частными производными и удовлетворяющая дифференциальному уравнению

(здесь 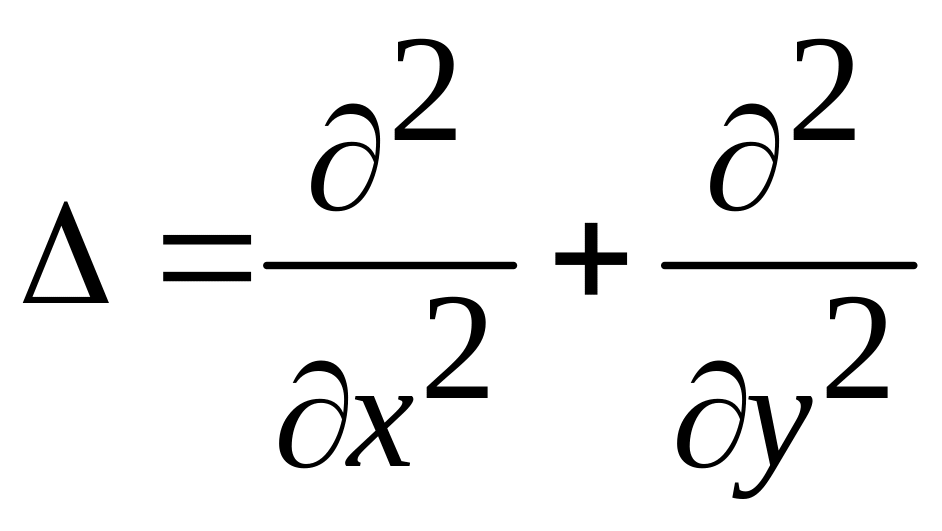- символ дифференциального оператора).

Это уравнение обычно называют уравнением Лапласа. Однако Лаплас рассмотрел его в 1782 г., а задолго до него это уравнение использовал Л. Эйлер в своих работах по гидродинамике.

Заметим, что в силу линейности уравнения Лапласа любая линейная комбинация гармонических функций является гармонической функцией.

Гармонические функции весьма популярны в приложениях: потенциалы важнейших векторных полей, рассматриваемых в физике, являются гармоническими функциями, и любую гармоническую функцию можно представить физически как потенциал некоторого поля.

Поэтому очень часто теорию гармонических функций называют теорией потенциала.

Установим связь между понятиями аналитических и гармонических функций. Эта связь выражается двумя простыми теоремами.

Теорема 2. Действительная и мнимая части произвольной функции , однозначной и аналитической в области D, являются в этой области гармоническими функциями.

Так как аналитические функции обладают производными любого порядка, то условия Даламбера-Эйлера можно дифференцировать по x и y . Продифференцировав первое из них по x, второе – по у, в силу теоремы о смешанных производных получим , .

Две гармонические в области D функции и , связанные условиями Даламбера-Эйлера, называются сопряженными.

Теорема 3. Для всякой функции , гармонической в односвязной области D, можно найти сопряженную с ней гармоническую функцию .

Рассмотрим интеграл

, где - фиксированная, а - переменная точка области D. В силу уравнения Лапласа

, этот интеграл не зависит от пути интегрирования и является функцией только точки z. Пользуясь свойствами криволинейных интегралов, получим , . Следовательно, функция и является искомой, сопряженной с . Так как функция определяется своими частными производными с точностью до постоянного слагаемого, то совокупность всех гармонических функций, сопряженных с , задается формулой

, где с – произвольная действительная постоянная.

В многосвязной области интеграл определяет, вообще говоря, многозначную функцию. Интеграл может принимать различные значения вдоль путей L и , соединяющих точки и z, если эти пути нельзя деформировать друг в друга, т.е. если внутри области, ограниченной L и , имеются точки не принадлежащие D.

При практическом восстановлении аналитической функции по её действительной (или мнимой) части можно воспользоваться следующим рассуждением.

Пусть, функция удовлетворяет соотношению . На условия Даламбера-Эйлера смотрим как на систему дифференциальных уравнений в частных производных первого порядка относительно неизвестной функции :

.

Из первого уравнения следует, что

так как по частному дифференциалу функция восстанавливается с точностью до слагаемого, зависящего от переменной y (вспомните, что по теореме о первообразной функция восстанавливается по полному дифференциалу с точностью до аддитивной постоянной). При вычислении интеграла, y – считается постоянным параметром.

Из второго условия Даламбера-Эйлера получим

В силу гармоничности

Таким образом,

Постоянную с можно вычислить, если известно значение восстанавливаемой функции в некоторой точке : .

Пример 1. Найти аналитическую функцию по известной ее части и дополнительном условии .

Решаем с помощью уравнений Даламбера-Эйлера:

функция φ(x) пока неизвестна. Дифференцируя по x и используя второе из условий аналитичности, получим

откуда а значит , Итак, , и, следовательно,

Здесь мы воспользовались определением показательной функции. Постоянную с найдем из условия , т.е.