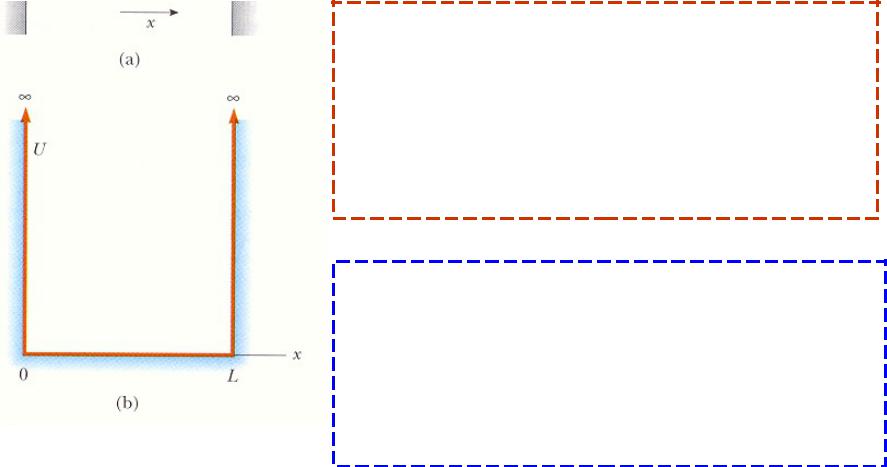
Частица в потенциальной яме
Внутри ямы:
Независимость потенциальной энергии системы «частица - окружающая среда» от положения частицы в яме.
Возможность считать потенциальную энергию системы в яме равной нулю.
Вне ямы:
Равенство волновой функции нулю. Отсутствие частицы.
Бесконечно большая потенциальная энергия системы.
31
Частица в потенциальной яме
Возможность представления волновой функции частицы
вяме в виде действительной синусоидальной функции
- длина волны де Бройля частицы.
|
|
|
|
|
|
2 x |
. |
|
|
x |
A |
sin |
|
|
|||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
Требование удовлетворения волновой функцией граничных условий на стенках ямы:
|
2 0 |
|
0 |
0 Asin |
|
|
|
|
|
|
выполняется всегда
L 0 |
|
2 L |
|
Asin |
|
|
|
|
|
|
|
2 L 2L
выполняется, если n n n = 1, 2, 3, …
Разрешены только определенные значения длин волн частицы !!!
Соответствие каждой из разрешенных длин волн квантовому состоянию системы и квантовому числу n.
32
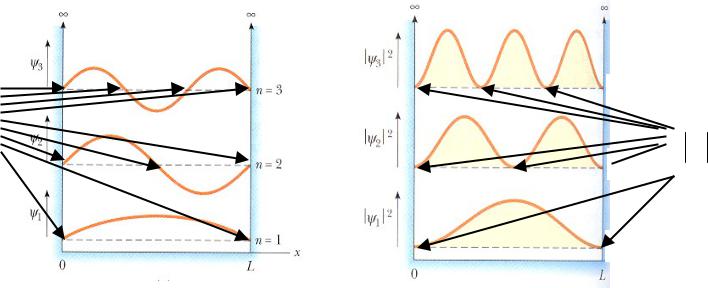
Частица в потенциальной яме
Волновая функция в терминах квантовых чисел
|
2 x |
|
2 x |
|
n x |
|||
x Asin |
|
|
Asin |
|
|
Asin |
L |
. |
|
||||||||
|
|
|
2L / n |
|
|
|||
Графическое представление
0
Возможные значения:
0 |
0 |
0 |
от х и 
2 от x для n = 1, 2 и 3.
n = 3
2 0
n = 2
|
|
|
|
|
|
|
|
|
|
n = 1 |
|
|
|
|
2 |
0 |
|
|
|
|
2 плотность вероятности |
|
|
|
|
|||||||
|
|
|
|
2 |
0 |
не имеет физического смысла |
||||
|
|
|||||||||
|
|
|
|
|
|
33 |
||||
|
|
|
|
|
|
|||||
Частица в потенциальной яме
Ограничение величин длин волн частицы yсловием 2nL ,
- возможность принятия импульсом частицы только определенных значений
p |
h |
|
h |
nh |
|
|
2L / n |
||||
|
|
2L |
Равенство нулю потенциальной энергии системы при нахождении частицы в яме.
Разрешенные значения энергии системы, равной кинетической энергии частицы,
|
|
|
1 |
|
|
|
p |
2 |
|
nh / 2L |
2 |
|
h |
2 |
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
E |
n |
|
|
mv |
|
|
|
|
|
|
|
En |
|
2 |
|
n |
|
n = 1, 2, 3, . . . |
|
|
2 |
|
|
|
2m |
|
2m |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
8mL |
|
|
|
|
|||||
Квантование энергии частицы!!!
34
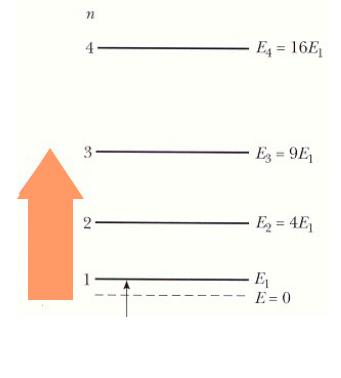
Частица в потенциальной яме
Соответствие минимальной разрешенной энергии состоянию
|
n = 1 |
E1 = h2/8mL2 |
|||
Энергия |
Энергия возбужденных состояний |
||||
n = 2 |
E2 |
= 4E1 |
|||
|
|||||
|
n = 3 |
E3 |
= 9E1 |
||
|
n = 4 |
E4 |
= 16E1 |
||
|
. . . . . . . . . . . . . . . . . . . . . . |
|
|||
Энергия основного состояния > 0 |
|
E |
= n2E |
1 |
|
|
|
||||
|
|
n |
|
||
n = 0, при котором E = 0 - не разрешено.
Наименьшая энергия, которой может обладать частица, - энергия основного состояния (n = 1).
35
Частица в потенциальной яме
Квантово-механические представления: частица никогда не находится в состоянии покоя.
Классические представления: возможность существования состояния с E = 0,
также как и состояний со всеми другими значениями энергии E.
Противоречие квантово-механического утверждения классическим представлениям!!!
36
Контрольный вопрос
Электрон, протон и альфа-частица помещены в отдельные, но идентичные потенциальные ямы.
Наивысшая энергия в основном состоянии будет соответствовать
(a)электрону (б) протону (в) альфа-частице
(г) энергия основного состояния одинакова для упомянутых частиц.
37