Основные положения квантовой механики
Э-м излучение с корпускулярной точки зрения
Связь вероятности обнаружения фотона
с числом N фотонов в единице объема данной
области пространства в данный момент времени:
Связь числа фотонов в единице объема с интенсивностью I излучения:
Вероятность N
VV
VN I
Связь интенсивности I э-м излучения |
I E2 |
|
с квадратом амплитуды E э-м волны |
||
|
Вероятность E2 
V
Пропорциональность вероятности обнаружения связанной с э-м излучением частицы (фотона) в единице исследуемого объема
квадрату амплитуды связанной с этим излучением э-м волны.
21
Основные положения квантовой механики
Общий случай квантовой частицы –
пропорциональность вероятности обнаружения частицы в единице объема квадрату амплитуды волны, представляющей частицу.
Амплитуда волны, связанной с частицей, - вероятностная амплитуда или волновая функция .
Зависимость полной волновой функции системы |
r1 ,r2 ,r3 ,...r,j ,...t,. |
от расположения частиц в системе и от времени |
Возможность математического разделения волновой функции для многих
исследуемых систем на пространственную и временную составляющие
|
|
|
|
|
,...t, |
|
|
|
|
r1 |
,r2 |
,r3 |
,...r,j |
rj e i t , |
|
|
|
где 2 f |
- угловая частота волновой функции и i |
|
. |
|||||
1 |
||||||||
22
Основные положения квантовой механики
Система с постоянной во времени потенциальной энергией
-содержание важной информации только
впространственной части волновой функции.
- часто комплексная величина * - комплексно сопряженная
2 * - всегда действителен, положителен и пропорционален
вероятности обнаружения частицы в данной точке единицы объема пространства в данный момент времени.
Содержание в волновой функции всей информации, которая только может быть известна о частице.
Немецкий физик Maкс Борн (1882-1970): вероятностная интерпретация волновой функции в 1928 году
(1954 г. – Нобелевская премия за выдающиеся успехи в области квантовой механики).
Основные положения квантовой механики
Предположение: у идеальной свободной частицы точно известный импульс px.
Волновая функция частицы – непрерывная синусоидальная волна длины = h / px.
Одинаковая вероятность обнаружения частицы в любой точке на оси x.
Волновая функция частицы, движущейся вдоль оси x, x Aeikx , где k = 2 / - волновое число частицы и A – постоянная амплитуда.
Невозможность измерения , возможность измерения реальной величины 
2 .
24
Основные положения квантовой механики
Если - волновая функция изолированной частицы, то
2 - относительная вероятность обнаружения частицы в произвольной
точке единицы объема пространства (плотность вероятности).
Если dV – малый элемент объема, окружающий некоторую точку,
то вероятность обнаружения частицы в этом объеме -
2 dV .
25
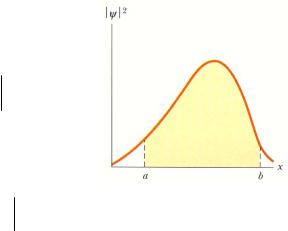
Основные положения квантовой механики
Одномерная волновая функция и вероятностные значения
Вероятность обнаружения частицы в пределах |
|
|
|
|
|
|
2 dx. |
||||
бесконечно малого интервала dx около точки x, P x dx |
|
|
|
||||||||
|
|
||||||||||
Вероятность обнаружения частицы в |
b |
2dx. |
|
|
|||||||
ab |
|
|
|
||||||||
пределах произвольного интервала a x P |
|
|
|
||||||||
b |
a |
|
|
|
|
|
|
|
|||
Сумма вероятностей обнаружения |
|
|
|
2dx 1. |
|
|
|||||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|||||||
частицы в целом где-либо на оси x |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||||
Нормированная функция - любая функция, удовлетворяющая это уравнение.
Выполнение условия нормировки – свидетельство существования частицы в некоторой точке пространства.
26
Основные положения квантовой механики
Одномерная волновая функция и вероятностные значения
Возможность получения всех измеряемых характеристик частицы, таких как энергия и импульс, если известна .
Вероятностное значение x - среднее положение, где можно |
|
ожидать обнаружения частицы после многочисленных измерений, x |
|
* x dx. |
|
... обозначение вероятностных величин. |
|
|
Вероятностное значение произвольной функции f(x), связанной с частицей,
f x 
* f x dx.
27
Основные положения квантовой механики
Одномерная волновая функция и вероятностные значения
Важные математические свойства
имеющей физический смысл волновой функции (x) системы:
•комплексная или действительная функция в зависимости от системы;
•определенная и однозначная во всех точках пространства;
•нормированная;
•непрерывная в пространстве (отсутствие скачков в значениях функции
влюбой точке пространства).
28
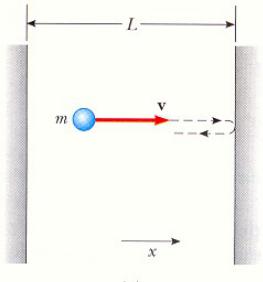
Частица в потенциальной яме
Проблема частицы в потенциальной яме – простая физическая проблема частицы, ограниченной в одномерном пространстве.
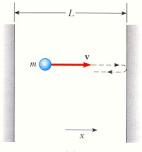
Движение частицы массы m
вдоль оси х со скоростью v
между двумя непроницаемыми стенками, отстоящими друг от друга на расстоянии
L.
29
Частица в потенциальной яме
Классическая физика:
отсутствие ограничений на значения импульса и энергии частицы.
Квантово-механическое приближение: требование нахождения волновой функции, удовлетворяющей условиям конкретной ситуации.
Стенки непроницаемы: нулевая вероятность обнаружения частицы вне ямы:
(x) = 0, если x < 0 и x > L.
Требование непрерывности волновой функции в пространстве.
(x) = 0 вне ямы:
требование равенства 0 волновой функции на стенках ямы - (0) = 0 и (L) = 0.
Физический смысл только у волновых функций, удовлетворяющих указанные граничные условия.
30