Содержание предыдущей лекции
Корпускулярно-волновой дуализм
Пересмотр дифракционного эксперимента с двумя щелями. Принцип неопределенности.
Квантовая механика
Основные положения квантовой механики.
Частица в потенциальной яме.
1
Контрольный вопрос
Электрон, протон и альфа-частица помещены в отдельные, но идентичные потенциальные ямы. Наивысшая энергия в основном состоянии будет соответствовать
(a) электрону (б) протону (в) альфа-частице (г) энергия основного состояния для упомянутых частиц одинакова.
|
|
|
h |
2 |
|
|
E |
|
|
|
n2 |
n 1 |
|
n |
|
2 |
||||
|
|
|
|
|||
|
|
|
8mL |
|
|
|
Из указанных частиц минимальной массой обладает электрон. Следовательно, его энергия в основном состоянии будет максимальной.
(a)
2
Содержание сегодняшней лекции
Квантовая механика
Уравнение Шредингера.
Частица в потенциальной яме со стенками конечной высоты. Прохождение (туннелирование) частицы через потенциальный энергетический барьер.
Сканирующий туннельный микроскоп. Простой гармонический осциллятор.
3
Уравнение Шредингера
1926: австрийский физик Эрнст Шредингер (1887-1961) волновое уравнение, описывающее изменения волновой функции в пространстве и времени, –
уравнение Шредингера
|
2 |
|
|
|
|
2 U i |
t |
2m |
|||
m – масса частицы, |
2 – оператор Лапласа. |
||
U – потенциальная энергия, |
|||
i – мнимая единица,
Декартова система координат (x, y, z): 2 2 2 2
x2 y2 z2
4
Уравнение Шредингера
•фундаментальное уравнение нерелятивистской квантовой механики,
•не может быть получено из других уравнений,
•его справедливость доказана тем, что все его выводы полностью согласуются с экспериментальными результатами,
•получено на основе оптико-механической аналогии (подобие между уравнениями, описывающими траектории лучей света
ичастиц в аналитической механике).
5
Уравнение Шредингера
Необходимость нахождения решения уравнения с учетом граничных условий для анализа поведения квантово-механической системы.
Решение уравнения – набор разрешенных волновых функций и энергетических уровней системы.
6
Уравнение Шредингера
Движение частицы в постоянном силовом поле
Независимость U от времени.
Постоянство общей энергии E частицы.
|
|
|
E |
|
|
где E – постоянная, равная |
||
Волновая функция x,y,z,t x,y,z exp |
i |
|
|
|
t , |
общей энергии системы |
||
|
|
|||||||
|
|
|
|
|
(частица и ее окружение). |
|||
|
|
|
2 |
|
|
|||
Уравнение Шредингера |
|
|
|
2 |
U i |
|||
2m |
||||||||
|
|
|
t |
|||||
2 E
exp i t 2 U exp 2m
iE t i
|
E |
|
|
E |
|
|
|
|
|
|
exp |
|
|
|
|
i |
|
|
|
i |
|
t |
|
|
|
|
|
|
|||
|
|
|
|
|
|||
|
2 |
2 U E |
- независящее от времени уравнение Шредингера. |
|
2m |
||||
|
|
|
7
Уравнение Шредингера
Согласие уравнения Шредингера с законом сохранения механической энергии: постоянство общей энергия изолированной системы.
Кинетическая энергия
свободной частицы или
частицы в потенциальной
яме, умноженная на 
волновую функцию
|
2 d 2 |
U E |
Постоянство общей энергии |
2m dx2 |
K U E constant |
Потенциальная энергия свободной частицы или частицы в потенциальной яме, умноженная на волновую функцию
Уравнение Шредингера - чрезвычайно успешное описание поведения атомных и ядерных систем, где классическая физика терпит
поражение.
Применение квантовой механики к макроскопическим объектам - результаты, аналогичные результатам, полученным в рамках классической
физики.
8
Уравнение Шредингера
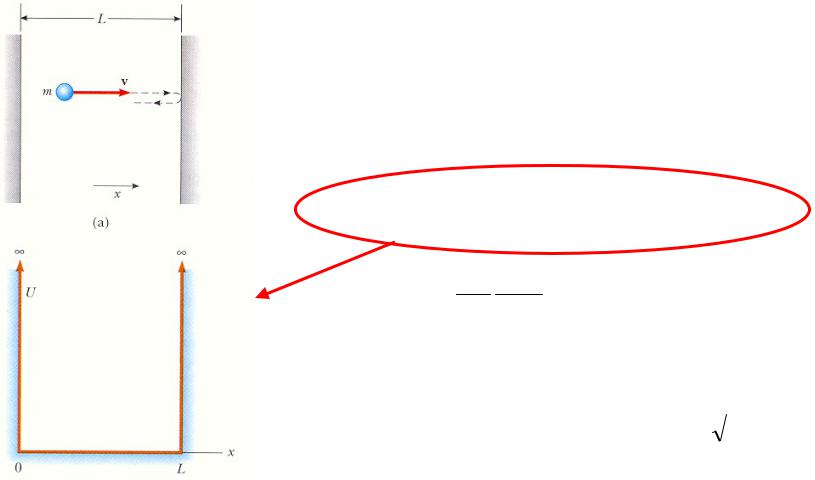
Частица в потенциальной яме (повторное рассмотрение)
Применение уравнения Шредингера для случая частицы в одномерной потенциальной яме шириной L.
Прямоугольная потенциальная яма – область, ограниченная направленной вверх кривой на диаграмме потенциальной энергии.
Прямоугольная потенциальная яма с бесконечно высокими стенками
2 d 2
2m dx2 U E
0 < x < L: U = 0
d 2 |
|
2mE |
|
|
|
|
. |
||
|
k 2 , |
где k |
|
2mE |
|
||||
dx2 |
2 |
||||||||
|
|
|
|||||||
|
|
|
|
|
|||||
9
Уравнение Шредингера
Частица в потенциальной яме (повторное рассмотрение) Общий вид решения x A sinkx B coskx,
A и B – постоянные, зависящие от граничных условий и условия нормировки.
1ое граничное условие: 0 0.
0 A sin0 B cos0 0 B 0 |
B = 0. |
2ое граничное условие: L 0.
L A sinkL 0 coskL 0
A = 0 – тривиальное решение (волновая функция везде равна 0).
Другое решение: kL = n , где n – целое число.
10