
- •Содержание предыдущей лекции
- •Контрольный вопрос
- •Содержание сегодняшней лекции
- •Уравнение Шредингера
- •Уравнение Шредингера
- •Уравнение Шредингера
- •Уравнение Шредингера
- •Уравнение Шредингера
- •Уравнение Шредингера
- •Уравнение Шредингера
- •Уравнение Шредингера
- •Частица в потенциальной яме со стенками конечной высоты
- •Частица в потенциальной яме со стенками конечной высоты
- •Частица в потенциальной яме со стенками конечной высоты
- •Частица в потенциальной яме со стенками конечной высоты
- •Частица в потенциальной яме со стенками конечной высоты
- •Прохождение частицы через потенциальный барьер
- •Прохождение частицы через потенциальный барьер
- •Прохождение частицы через потенциальный барьер
- •Прохождение частицы через потенциальный барьер
- •Прохождение частицы через потенциальный барьер
- •Прохождение частицы через потенциальный барьер
- •Прохождение частицы через потенциальный барьер
- •Простой гармонический осциллятор
- •Простой гармонический осциллятор
- •Простой гармонический осциллятор
- •Простой гармонический осциллятор
- •АТОМНАЯ ФИЗИКА
- •Контрольный вопрос
Уравнение Шредингера
Частица в потенциальной яме (повторное рассмотрение)
k |
|
/ |
k n |
|
|
|
|
|
|
2mE |
|
|
|
|
|
|
|||
Соответствие каждому значению n |
|
|
|
h2 |
|
2 |
|||
определенного квантованного значения энергии |
E |
n |
|
|
n |
|
|||
2 |
|
||||||||
|
|
|
|
||||||
|
|
|
|
|
|
|
8mL |
|
|
Разрешенные волновые функции n x
Из условия нормировки 
 2dx 1
2dx 1
A sinn x .
L
A 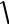
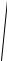 L2 .
L2 .
|
n x |
|
2 |
|
|
n x |
|
|
Значения нормированной волновой функции |
|
|
sin |
|
. |
|||
L |
L |
|||||||
|
|
|
|
|
|
11
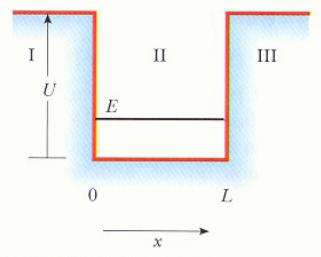
Частица в потенциальной яме со стенками конечной высоты
Предположение:
частица вне ямы - конечное значение U потенциальной энергии системы,
частица в яме – нулевое значение потенциальной энергии.
В яме общая энергия E системы «частица – яма» < U.
Классическая механика: постоянное нахождение частицы в яме.
Квантовая механика: существование конечной вероятности обнаружения частицы вне ямы, неравенство нулю волновой функции вне ямы.
Принцип неопределенности: неопределенное значение величины энергии системы.
Возможность нахождения частицы вне ямы до тех пор, пока любым возможным способом не будет обнаружено нарушение закона сохранения энергии.
12
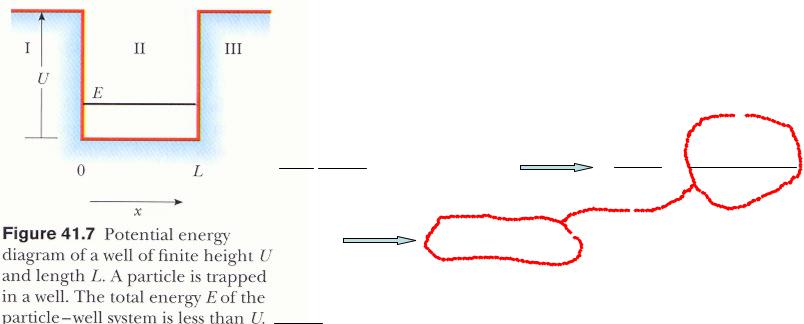
Частица в потенциальной яме со стенками конечной высоты
|
|
|
Область II: |
U = 0, |
|
|
|
разрешены синусоидальные волновые функции, |
|||||
|
|
граничные условия – отсутствие требования |
||||
|
|
|
равенства нулю на стенках ямы. |
|
||
|
|
|
Области I и III: |
2m U E |
|
|
|
2 d 2 |
U E |
d 2 |
|
||
|
2m dx2 |
|
dx2 |
2 |
|
|
U E |
|
коэффициент при д. б. > 0. |
|
|||
Области I и III: |
d 2 |
C 2 , где C 2 2m U E |
/ 2 const 0 |
|
||
dx2 |
|
|||||
|
|
|
|
|
|
|
Общее решение этого уравнения: AeCx Be Cx
13
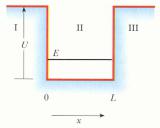
Частица в потенциальной яме со стенками конечной высоты
Общее решение AeCx Be Cx - начальная
точка
для нахождения решений, соответствующих областям I, II и III.
Область I (x < 0): В = 0 во избежание бесконечного значения .I AeCx - убывание по экспоненте.
Область II (0 <x < L): U = 0 – разрешены синусоидальные волновые
функции (решения уравнения Шредингера).
II x F sin kx G cos kx, где F и G - постоянные.
Область III (x > L): А = 0 во избежание бесконечного значения. III Be Cx - убывание по экспоненте.
14
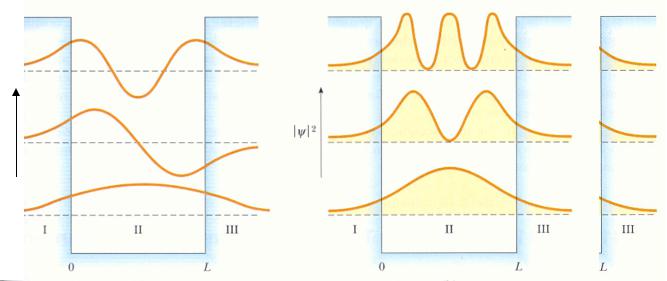
Частица в потенциальной яме со стенками конечной высоты
Волновые функции и плотности вероятности 
 2
2
Граничные условия: |
I II |
и |
|
d I |
|
|
|
d II |
|
при x = 0 |
|
dx |
|
dx |
|||||||
|
|
|
|
|
|
|
|
|||
|
II III |
и |
d II |
|
d III |
при x = L |
||||
|
|
dx |
||||||||
|
|
|
|
dx |
|
|
|
|
||
Достаточность этих граничных условий и условия нормировки для нахождения четырех коэффициентов A, B, F и G, а также разрешенных значений энергии E.
15

Частица в потенциальной яме со стенками конечной высоты
Действие квантовой точки - маленькой области, выращенной на поверхности кристалла кремния, в качестве потенциальной ямы для электронов.
Захват электронов на квантованных энергетических уровнях в квантовой точке.
Хранение двоичной информации с помощью квантовых точек – направление активных исследований.
Простая схема сохранения двоичной информации:
«единица» - в квантовой точке находится электрон, «нуль» - квантовая точка пуста.
16
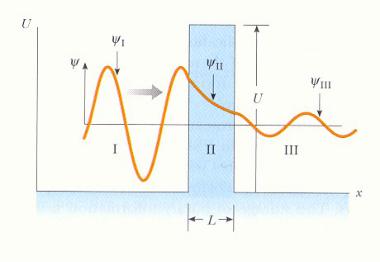
Прохождение частицы через потенциальный барьер
Потенциальный энергетический барьер – область, заключенная под кривой потенциальной энергии.
Квадратный барьер: постоянное значение потенциальной энергии U (высота барьера)
впределах барьера шириной L,
иравенство энергии нулю за пределами барьера.
Предположение: частица, обладающая энергией E < U,
приближается к барьеру конечной высоты и ширины слева.
Классическая механика: отражение частицы барьером.
Область II запрещена для частицы - кинетическая энергия частицы в ней
была бы отрицательной (E < U).
Квантовая механика:
доступность области II для частицы независимо от ее энергии.
17
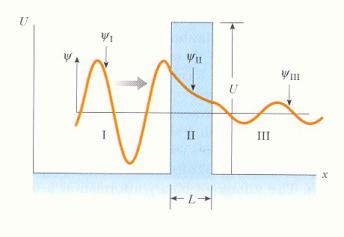
Прохождение частицы через потенциальный барьер
Классическая физика:
невозможность прохождения частицы в запрещенную область III.
Квантовая механика принцип неопределенности - частица может находиться внутри барьера
в течение очень короткого временного интервала.
Относительно узкий барьер:
достаточность временного интервала для прохождения частицы через барьер.
18
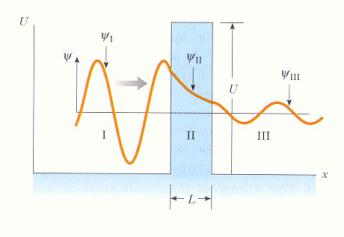
Прохождение частицы через потенциальный барьер
Области I, II и III:
наличие имеющих физический смысл решений уравнения Шредингера. Области I и III: синусоидальный вид решений.
Область II: экспоненциальный вид решения. Представление полного решения красной кривой.
Область III: вероятность обнаружения частицы за барьером не равна нулю.
Прохождение частицы через барьер – туннелирование сквозь барьер или проникновение через барьер.
19
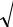
Прохождение частицы через потенциальный барьер
Описание вероятности туннелирования
с помощью коэффициентов прохождения T и отражения R.
T + R = 1
T << 1 (очень широкий или очень высокий барьер, т.е. U >> E):
T e 2CL, где |
|
|
|
|
C |
|
2m U E |
|
|
|
|
|
||
|
|
|
|
Квантовая модель проникновения частицы сквозь барьер: неравенство коэффициента T нулю.
Экспериментальные наблюдения явления туннелирования частиц сквозь энергетические барьеры –
дополнительные доказательства справедливости законов квантовой физики.
20
