fd02aed

7.ПОКАЗАТЕЛИ ДИАГНОСТИРОВАНИЯ

7.1.Ошибки диагностирования

Впроцессе диагностирования неизбежно возникают различного рода ошибки, которые в той или иной степени влияют на правильность принятия решения о техническом состоянии объекта.

Основными причинами ошибок диагностирования являются:

• неточное измерение и преобразование контролируемого па-

раметра;

• неточное сравнение измеренного значения параметра с ниж-

ним и верхним допустимыми пределами;

• ненадежное функционирование средств контроля в процессе диагностирования.

При диагностировании могут возникнуть ошибки первого и второго рода. Ошибка, относящаяся к диагнозу S1 (принимается решение о наличии диагноза S2, когда в действительности объект принадлежит диагнозу S1), называется ошибкой первого рода. Ошибка, относящаяся к диагнозу S2 (принимается решение в пользу диагноза S1, когда справедлив диагноз S2), называется ошибкой второго рода.

Считая состояние S1 исправным (работоспособным), а состояние S2 – неисправным (неработоспособным), легко понять, что ошибка первого рода является ложной тревогой, или ложным отказом, а ошибка второго рода – пропуском дефекта, или необнаруженным отказом. В дальнейшем будем обозначать вероятность ошибки первого рода буквой γ1, а вероятность ошибки второго ро-

да – γ2.

Поясним смысл вышеуказанных ошибок на конкретном примере. Пусть производится диагностирование объекта по одному параметру Y. Задача состоит в выборе значения Z0 параметра Z таким образом, что при Z > Z0 следует принимать решение о снятии объекта с эксплуатации, а при Z < Z0 – допустить дальнейшую эксплуатацию. По результатам технического диагностирования может быть принято одно из двух возможных решений:

•при Z < Z0 Z S1, т. е. объект признается исправным (работоспособным);

•при Z > Z0 Z S2, т. е. объект признается неисправным (неработоспособным).

361

С учетом ошибок диагностирования распределение значений параметра Z для исправных и неисправных объектов показано на рис. 7.1. Из рисунка видно, что области исправного S1 и неисправного S2 состояний пересекаются, потому принципиально невозможно выбрать значение Z0, при котором в результате технического диагностирования было бы принято безошибочное решение. Заштрихованные на рис. 7.1 площади под кривыми f (Z|S1) и f (Z|S2) характеризуют вероятности ошибочных решений при диагностировании объекта.

f (Z|Si)

S1 S2

Рис. 7.1.

Распределение плотности вероятности значений параметра Z для исправного S1 и неисправного S2 состояний объекта

Площадь под кривой плотности вероятности исправного состояния, соответствующая Z >Z0, выражает условную вероятность ситуации Z >Z0 для исправных объектов:

где P(Z > Z0|S1) – условная вероятность того, что исправный (работоспособный) объект в результате диагностирования признается неисправным (неработоспособным) (условная вероятность ошибки первого рода, обозначаемая символом γ1y).

Площадь под кривой плотности вероятности неисправного состояния, соответствующая Z < Z0, выражает условную вероятность ситуации Z < Z0 для неисправных объектов:

362

−∞

где P(Z<Z0|S2) – условная вероятность того, что неисправный (неработоспособный) объект в результате диагностирования признается исправным (работоспособным) (условная вероятность ошибки второго рода, обозначаемая символом γ2y).

Значения ошибок характеризуют качество процесса диагностирования в целом, а это значит, что они должны учитываться при задании и определении показателей диагностирования.

Это можно сделать следующим образом. Например, при измерении параметров во время диагностирования кривая рассеяния может занимать внутри поля допуска различные положения (рис. 7.2), и в этом случае нельзя определить, какому участку поля рассеяния они соответствуют. Так, например, точки А и В могут принадлежать к кривым 1 и 2, расположение которых может подтверждать годность объекта, но может относиться к кривым 1а и 2а (ошибки второго рода), в значительной части выходящими за пределы допуска, показывая тем самым брак контролируемого объекта (заштрихованные участки).

Для исключения опасности появления ошибок второго рода при контроле в случае, когда поле допуска превышает поле рассеяния, т. е. ω< δ , необходимо с помощью настройки обеспечить рас-

363

положение кривой фактического распределения размеров внутри поля допуска с таким расчетом, чтобы ее центр группирования (математическое ожидание Мx) отстоял от предельных размеров не менее чем на 3σ.

7.2. Показатели и характеристики диагностирования

Показатель диагностирования – это количественная характе-

ристика или параметр, описывающий одно или несколько свойств процесса диагностирования.

К показателям диагностирования относятся:

•достоверность технического диагностирования;

•вероятность ложного отказа при диагностировании;

•вероятность необнаруженного отказа при диагностировании. К характеристикам диагностирования относятся:

•продолжительность технического диагностирования;

•полнота технического диагностирования;

•глубина поиска места отказа.

Рассмотрим некоторые из этих показателей и характеристик более подробно.

7.2.1. Достоверность диагностирования

Достоверность диагностирования – это степень объективного соответствия результатов диагностирования действительному техническому состоянию объекта.

Достоверность диагностирования численно оценивается вероятностью того, что в конце цикла проверок всех параметров объекта система диагностирования выдает объективный результат. Достоверность обозначают символом D. Для ее вычисления рассмотрим задачу диагностирования с позиций общей теории проверки статистических гипотез.

Пусть имеется объект, состояние которого описывается значением параметра Y. Физическая природа этого параметра может быть различной для различных объектов, важно лишь то, что рассматриваемый параметр характеризует качество объекта, оцениваемое при диагностировании. Под воздействием различных производственных

364

и эксплуатационных факторов значение этого параметра изменяется случайным образом во времени и при переходе от объекта к объекту. В результате параметр Y можно рассматривать как случайную величину с плотностью распределения f (y). Для значений парамет-

В соответствии с этим условием могут быть высказаны две взаимоисключающие гипотезы: Н1 – объект работоспособен и Н2 – объект неработоспособен.

Априорные вероятности появления соответствующих событий равны:

Фактически Р(Н1) и Р(Н2) есть вероятности соответственно безотказной работы и отказа объекта до проведения диагностирова-

Возможно более точное разделение объектов этих двух категорий (работоспособных и неработоспособных) является конечной целью диагностирования. Однако в процессе диагностирования, как уже отмечалось, неизбежно появляются ошибки, в результате чего вместо истинного значения случайной величины Y наблюдается реализация другой случайной величины

Z = Y ±ε ,

где ε − случайная ошибка диагностирования. Это приводит к замене условия работоспособности 1 ≤ y ≤ 2 другим условием:

1 ≤ Z ≤ 2 .

Замена условия работоспособности приводит к ошибочным заключениям о годности объекта, в результате чего некоторая часть работоспособных объектов бракуется, а какая-то часть неработоспособных объектов рассматривается как работоспособная. Таким

365

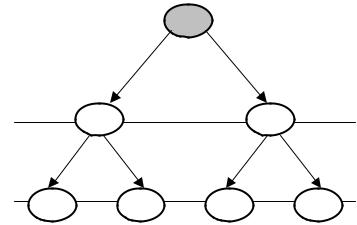
образом, при реальном диагностировании происходит одно из четырех несовместных событий (рис. 7.3): Н11 – истинное и измеренное значения параметра находятся в пределах поля допуска, т. е.

Рис. 7.3. Схема принятия решений при диагностировании

Н12 – истинное значение параметра находится в пределах допуска, измеренное значение – за его пределами, т. е.

1 ≤ y ≤ 2 ; Z > 2 или Z < 1 ;

Н22 – истинное и измеренное значения параметра находятся за пределами допуска, т.е.

y > 2 или y < 1 ; Z > 2 или Z < 1 ;

Н21 – истинное значение параметра находится за пределами допуска, измеренное значение – в пределах допуска, т. е.

События Н11 и Н22 характеризуют правильные решения, поэтому назовем их объективной работоспособностью (ОР) и объективным отказом (ОО), а соответствующие им вероятности Р(Н11) = Рор

366

иР(Н22) = Роо – вероятностями объективной работоспособности

иобъективного отказа.

События Н12 и Н21 характеризуют ошибочные решения. Событие Н12 соответствует ложному отказу (ЛО), а событие Н21 – необнаруженному отказу (НО). Этим событиям соответствуют Р(Н12) = Рло и Р(Н21) = Рно – вероятности ложного и необнаруженного отказов.

Вероятность ложного отказа Рло – это вероятность получения решения «негоден» при контроле параметра, значение которого в действительности соответствует требованиям технической документации. Этой вероятностью оценивается совместное наступление двух событий:

• первое – объект находится в работоспособном состоянии, вероятность этого события Р(Н1 ) = Р( 1 ≤ y ≤ 2 );

• второе – система диагностирования оценивает работоспособный объект как отказавший. Вероятность появления этого события оценивается величиной γ1y – условной вероятностью появления ошибки «негоден». Вероятность ложного отказа задается выражением

Вероятность необнаруженного отказа Рно – это вероятность получения решения «годен» при контроле параметра, значение которого в действительности не соответствует требованиям технической документации. Этой вероятностью оценивается совместное наступление следующих двух событий:

• первое – объект находится в неработоспособном состоянии,

вероятность этого события Р(Н2 ) =1 − Р(Н1 ) =1 – Р ( 1 ≤ y ≤ 2 );

• второе – система диагностирования оценивает неработоспособный объект как работоспособный. Вероятность этого события оценивается величиной γ2y – условной вероятностью появления ошибки «годен». Для одностороннего допуска на параметр Y эта вероятность задается формулой (7.2). Таким образом,

Учитывая соотношения (7.3) и (7.4), схему возможных результатов диагностирования можно представить в виде схемы, изобра-

367

женной на рис. 7.4. Ошибки, соответствующие событиям Н12 и Н21, принято называть ошибками 1-го рода (риск изготовителя) и 2-го рода (риск заказчика). Как уже отмечалось, ошибка 1-го рода обозначается символом γ1, а ошибка 2-го рода − γ2.

Рис. 7.4. Схема возможных результатов диагностирования

Вероятности Рло = Р(Н12) = γ1 и Рно = Р(Н21) = γ2 являются естественной мерой недостоверности полученных результатов. Они мо-

гут быть непосредственно использованы как критерий достоверности, однако для характеристики качества диагностирования лучше использовать вероятность правильного решения, соответствующую двум исходам Н11 и Н22:

Dд = P (H11 )+ P (H22 ) =1− P (H12 )− P (H21 ) =1− γ1 − γ2 , (7.8)

где Dд − достоверность диагностирования объекта.

В ряде случаев события ложного отказа (ошибки 1-го рода) и необнаруженного отказа (ошибки 2-го рода) неравноценны по ожидаемым последствиям. В этих случаях необходимо оценивать отдельно степень доверия к решениям «объект годен» и «объ-

368

ект негоден» с помощью соотношений, получаемых из формулы Байеса ( 4.19):

Введем обозначения:

S1 – событие, заключающееся в том, что объект находится в работоспособном состоянии;

S2 – событие, заключающееся в том, что объект находится в неработоспособном состоянии;

Z1 – событие, заключающееся в том, что при диагностировании

С учетом введенных обозначений из формулы (7.9) получается следующее выражение для достоверности результата «объект годен»:

Учитывая, что P(S1) = P(H1), P(Z1/S1) = 1 – γ1y, P(S2) = P(H2) = 1 –

–P(H1), P(Z1|S2) = γ2y, окончательно получим

Аналогично получаем выражение для достоверности результата «объект негоден»:

369

В формулах (7.10) и (7.11) γ1y – условная вероятность ошибки 1-го рода, γ2y – условная вероятность ошибки 2-го рода.

Совокупность показателей достоверности (7.9)…(7.11) обеспечивает оценку качества диагностирования объекта. Из этих выражений видно, что достоверность диагностирования тем больше, чем

меньше Рло и Рно. А поскольку Рло = Р(Н1) γ1y и Рно = Р(Н2) γ2y, отсюда следует вывод, что для повышения достоверности диагности-

рования необходимо уменьшать условные вероятности ошибок γ1y и γ2y (при заданной надежности объекта). В идеальном случае при γ1y = γ2y = 0 достоверность диагностирования Dд = 1. Зная вероятности появления событий Н11, Н12, Н22, Н21, можно произвести соответствующие вычисления достоверности решений, принимаемых в процессе диагностирования.

7.2.2. Вероятность ложного отказа

Вероятность ложного отказа задается формулой (7.6):

Pло = P (H12 )= Р(Н1 ) γ1y .

В общем случае, исходя из смысла события Н12, выражение для вероятности ложного отказа записывается в виде

где f (y) – плотность распределения истинного значения контролируемого параметра объекта; f(z) − плотность распределения измеренного значения контролируемого параметра объекта (z = y ± ε ).

370