ТФКП тест
.pdf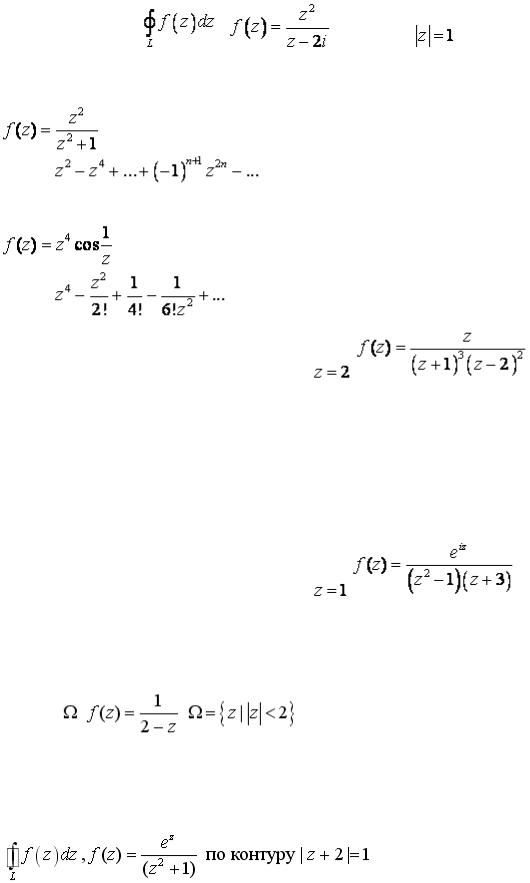
Вопрос: Вычислить |
, |
по контуру |
Ответ: 0 |
|
|
Вопрос: Разложить в ряд Тейлора указанную функцию 
в окрестности точки 
,
Ответ:
Вопрос: Разложить в ряд Лорана указанную функцию 
в окрестности точки 
,
Ответ:
Вопрос: Найти вычет функции 
в точке
Ответ: 
Вопрос: Если 
, 
то в каждой точке дифференцируемости функции выполняются равенства (Коши - Римана)
Ответ: 
Вопрос: Найти вычет функции 
в точке
Ответ: 
Вопрос: Разложить в ряд Лорана указанную функцию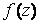 
по степеням z в заданной
области
Ответ: 
Вопрос: Найти интеграл от заданной функции по заданному контуру. Обход осуществляется против часовой стрелки.
Ответ: 0
Вопрос: Определите модуль 
и аргумент 
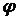комплексного числа 
.
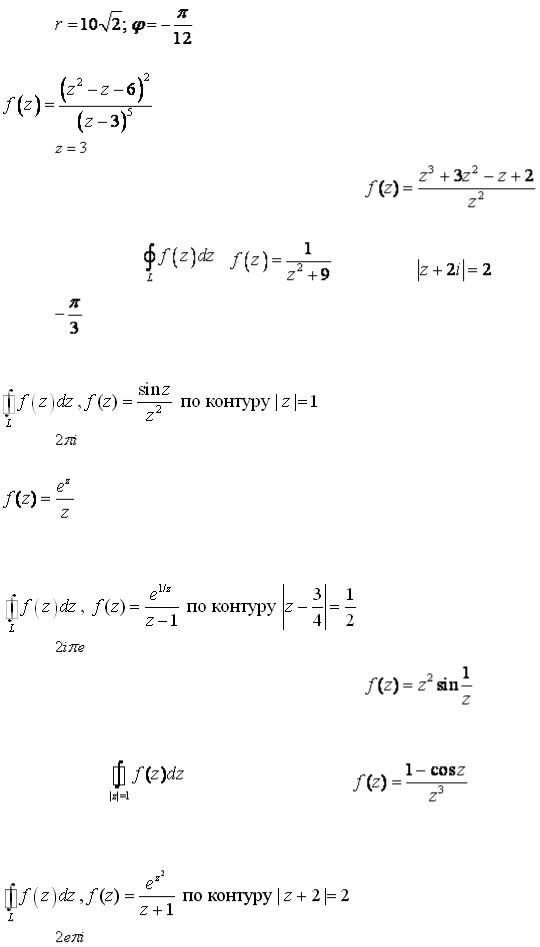
Ответ:
Вопрос: Определить характер особой точки и саму особую точку для заданной функции
Ответ: - полюс третьего порядка
Вопрос: Найти вычет функции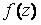 
в точке 
,
Ответ: 
Вопрос: Вычислить |
, |
по контуру |
Ответ:
Вопрос: Найти интеграл от заданной функции по заданному контуру. Обход осуществляется против часовой стрелки.
Ответ:
Вопрос: В каких точках заданная функция является дифференцируемой?
Ответ: в каждой комплексной точке Вопрос: Найти интеграл от заданной функции по заданному контуру. Обход осуществляется против часовой стрелки.
Ответ:
Вопрос: Найти вычет функции 
в точке 
,
Ответ: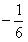 
Вопрос: Найти |
для заданной функции, |
Ответ: 
Вопрос: Найти интеграл от заданной функции по заданному контуру. Обход осуществляется против часовой стрелки.
Ответ:
Вопрос: Найти интеграл от заданной функции по заданному контуру. Обход
осуществляется против часовой стрелки.
Ответ:
Вопрос: Определить характер особой точки и саму особую точку для заданной функции
Ответ: –простой полюс Вопрос: Определить характер особой точки и саму особую точку для заданной функции
Ответ: простые полюса Вопрос: В каких точках заданная функция является дифференцируемой?
Ответ: на мнимой оси Вопрос: Найти интеграл от заданной функции по заданному контуру. Обход
осуществляется против часовой стрелки.
Ответ:
Вопрос: Функция 
называется гармонической в области D, если она имеет в ней непрерывные частные производные второго порядка и удовлетворяет в этой области уравнению Лапласа
Ответ: 
Вопрос: Найти |
для заданной функции, |
, где |
Ответ: |
|
|
Вопрос: Найти |
для заданной функции, |
, где |
Ответ: 
Вопрос: В каких точках заданная функция является дифференцируемой?
Ответ: в каждой комплексной точке Вопрос: Определить характер особой точки и саму особую точку для заданной функции
Ответ: в точке |
полюс второго порядка |
Вопрос: Найти вычет функции 
в точке
Ответ: 1
Вопрос: Определите все комплексные решения уравнения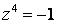 
.
Ответ: |
|
|
Вопрос: Найти |
для заданной функции, |
|
Ответ: |
|
|
Вопрос: Вычислить |
, |
по контуру |
Ответ: |
|
|
Вопрос: Найти вычет функции |
в точке |
|
Ответ:
Вопрос: Определить характер особой точки и саму особую точку для заданной функции
Ответ: в точке 
полюс первого порядка Вопрос: В каких точках заданная функция является аналитической?
Ответ: ни в одной точке
Вопрос: Найти вычет функции 
в точке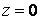 
, 
Ответ: 1
Вопрос: Найти интеграл от заданной функции по заданному контуру. Обход осуществляется против часовой стрелки.
Ответ:
Вопрос: Определить характер особой точки и саму особую точку для заданной функции
Ответ: - полюс третьего порядка
Вопрос: Вычетом функции 
в изолированной особой точке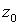 
называется
Ответ: коэффициент 
в разложении в ряд Лорана
Вопрос: Найти |
для заданной функции, |
, где |
Ответ: 
Вопрос: Найти вычет функции 
в точке 
,
Ответ: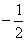 
Вопрос: Вычислить |
, |
по контуру |
Ответ:
Вопрос: Разложить в ряд Лорана указанную функцию 
по степеням 
в заданной области 
Ответ:
Вопрос: В каких точках заданная функция является аналитической?
Ответ: всюду, кроме точек 
и 
Вопрос: Определить характер особой точки и саму особую точку для заданной функции
Ответ: - полюс третьего порядка Вопрос: Найти интеграл от заданной функции по заданному контуру. Обход осуществляется против часовой стрелки.
Ответ:
Вопрос: В каких точках заданная функция является дифференцируемой?
Ответ: ни в одной точке
Вопрос: Найти |
для заданной функции, |
|
, где |
Ответ: |
|
|
|
Вопрос: Вычислите определитель |
где |
. |
|
Ответ:
Вопрос: Если 
- аналитическая функция в односвязной области D, то значение
интеграла Ответ: не зависит от линии Г интегрирования, а только от координат начальной и
конечной точки этой линии Вопрос: В каких точках заданная функция является аналитической?
Ответ: в каждой комплексной точке Вопрос: Определить характер особой точки и саму особую точку для заданной функции
Ответ: |
- полюс второго порядка |
|
|
Вопрос: Найти |
для заданной функции, |
, где |
|
Ответ: 
Вопрос: Определить характер особой точки и саму особую точку для заданной функции
Ответ: |
- простой полюс |
|
|
Вопрос: Вычислить |
, |
по контуру |
|
Ответ:
Вопрос: Разложить в ряд Тейлора указанную функцию 
в окрестности точки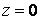 
,
Ответ: |
|
|
Вопрос: Вычислить |
, |
по контуру |
Ответ: 0
Вопрос: Вычислите действительную 
и мнимую 
части комплексного числа
.
Ответ: 
Вопрос: Определите модуль и аргумент комплексного числа |
. |
Ответ:
Вопрос: Функция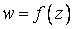 
является аналитической в бесконечно удаленной точке 
, если функция
Ответ: |
аналитична в точке |
|
|
Вопрос: Вычислите определитель |
где |
. |
|
Ответ: |
|
|
|
Вопрос: Найти вычет функции 
в точке
Ответ: 0
Вопрос: Определите все комплексные решения уравнения 
.
Ответ: |
|
|
Вопрос: Найти |
для заданной функции, |
|
Ответ: 0 |
|
|
Вопрос: Найти |
для заданной функции, |
|
Ответ: |
|
|
Вопрос: Вычислить |
, |
по контуру |
Ответ:
Вопрос: Найти вычет функции 
в точке
Ответ: 0
Вопрос: Разложить в ряд Лорана указанную функцию 
по степеням 
в заданной
области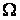 
Ответ:
Вопрос: Функция 
при 
раскладывается в ряд Тейлора.
Ответ:
Вопрос: Найти вычет функции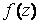 
в точке
Ответ: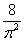 
Вопрос: Определить характер особой точки и саму особую точку для заданной функции
Ответ: – существенно особая точка Вопрос: В каких точках заданная функция является аналитической?
Ответ: всюду, кроме точки
Вопрос: Для всякой аналитической функции 
производная 
выражается через частные производные функций 
и 
Ответ:
Вопрос: В каких точках заданная функция является аналитической?
Ответ: в каждой комплексной точке z
Вопрос: Найти вычет функции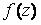 
в точке
Ответ: 
Вопрос: Найти |
для заданной функции, |
, где |
Ответ: 
Вопрос: Вычислить |
, |
по контуру |
Ответ:
Вопрос: Определить характер особой точки и саму особую точку для заданной функции
Ответ: - простой полюс
Вопрос: Определите модуль и аргумент комплексного числа |
. |
Ответ:
Вопрос: Определить характер особой точки и саму особую точку для заданной функции
Ответ: – правильная точка Вопрос: В каких точках заданная функция является дифференцируемой?
Ответ: всюду, кроме точки 
Вопрос: В каких точках заданная функция является аналитической?
Ответ: всюду, кроме точек 
и 
Вопрос: Найти |
для заданной функции, |
, где |
Ответ: |
|
|
Вопрос: Найти |
для заданной функции, |
|
Ответ: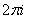 
Вопрос: Определить характер особой точки и саму особую точку для заданной функции
Ответ: –простой полюс Вопрос: В каких точках заданная функция является аналитической?
Ответ: всюду, кроме точек 
и 
Вопрос: В каких точках заданная функция является дифференцируемой?
Ответ: в каждой комплексной точке
Вопрос: Вычислить |
, |
по контуру |
Ответ:
Вопрос: Функция 
аналитическая в кольце представляется в этом кольце сходящимся рядом Лорана
Ответ: |
|
|
Вопрос: Найти |
для заданной функции, |
, где |
Ответ: 
Вопрос: Определите все комплексные решения уравнения 
.
Ответ: 
Вопрос: В каких точках заданная функция является дифференцируемой?
Ответ: в каждой комплексной точке
Вопрос: Вычислить |
, |
по контуру |
Ответ: 
Вопрос: Определить характер особой точки и саму особую точку для заданной функции
Ответ: –правильная точка Вопрос: В каких точках заданная функция является аналитической?
Ответ: ни в одной точке Вопрос: Определить характер особой точки и саму особую точку для заданной функции