10. Формат числа с плавающей запятой, его особенности.
Разрядная сетка для этих чисел имеет две группы: первая группа обозначает порядок числа, а другая – мантиссу.
Для изображения двоичных чисел с плавающей запятой используется выражение
А = 2P*М. (2)
где P – порядок числа (целое число);
M – мантисса числа (дробное число);
2P − часть числа, называемая его характеристикой; она выражена в логарифмической форме, поэтому такое представление числа часто называют полулогарифмическим. Значение Р со знаком указывает истинное положение запятой в числе А: умножение (деление) двоичного числа на 2 соответствует сдвигу запятой на один разряд вправо (влево). Аналогия − умножение (деление) десятичного числа на 10. Например: (111,0)2*2=(1110).
Отсюда произвольные двоичные числа в полулогарифмическом виде можно записать:
101001,111 = 26 * 0,101001111;
101,001111 = 23 * 0,101001111;
0,00101001111 = 2-2 * 0,101001111.
В левой части приведенных равенств стоят истинные значения чисел в двоичном коде, а в правой – их представления в формате с плавающей запятой. Из правых частей видно, что числа имеют одинаковые мантиссы, но, вследствие различных порядков для этих чисел, положение запятой в них неодинаково. Таким образом, с помощью порядка можно изменить истинное положение запятой в числе. Отсюда и название “плавающая запятая”.
Нормализованные числа - двоичные числа, у которых в старшем разряде мантиссы стоит единица; они используются в формате числа с плавающей запятой для того, чтобы наиболее полно использовать разряды мантиссы для повышения точности представления чисел. У нормализованных чисел мантисса находится в пределах 1/ 2 £ M <1 (старший разряд − 1/2).
Рассмотрим две записи числа 41,75 в двоичной системе счисления в форме с плавающей запятой, когда под мантиссу отведено 8 двоичных разрядов:
101001,11 = 26* 0,10100111 - нормализованное число (41,75);
101001,11 = 28* 0,00101001(11) - ненормализованное число (41,0).
Из сравнения двух записей одного числа следует, что использование нормализованных чисел увеличивает точность вычислений, так как разряды, отведенные для мантиссы числа, используются полностью.
Из выражения (2) следует: количество разрядов, отводимых для мантиссы (n), зависит точность записи чисел, см. (1); количества разрядов, используемых для хранения порядка (m), зависит диапазон записываемых чисел (при достаточно больших n, обычно n≥30):
2-2 £ < 22 -1 m m
A . (3)
Основное достоинство формата чисел с плавающей запятой - отсутствие масштабных коэффициентов в связи с большим диапазоном представляемых чисел (современные форматы представляют 80-разрядные двоичные числа: 64 - мантисса и 16 - порядок числа). Основной недостаток (в сравнении с фиксированной запятой) – необходимость отдельных схем для выполнения операций как над мантиссами, так и над порядками чисел.
Скорость выполнения операций сложения и вычитания чисел с фиксированной запятой выше, чем чисел с плавающей запятой.
11. Двоично-десятичный формат числа.
12. Прямой, обратный и дополнительный коды двоичных чисел, упрощенные правила перевода чисел в обратный и дополнительный коды.
Прямой код двоичного числа является представлением абсолютного значения числа с кодированным знаком и определяется выражением:
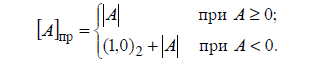
Обратный код двоичного числа является дополнением модуля числа до числа,
соответствующего полностью заполненной разрядной сетке, т.е. до величины 1,111…1 или до (10)2 – 1*2-m, где 1*2-m - единица младшего разряда.
Обратный код числа определяется выражением:
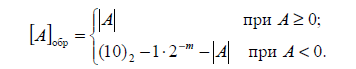
Например, обратные коды чисел А1 = 0,11010 и А2 = -0,11010 будут иметь вид
[А1]обр = 011010; [А2]обр = 100101.
Дополнительный код двоичного числа является дополнением модуля числа до двух и определяется выражением:
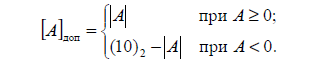
Дополнительный код = Обратный код + 1мл. р.
Например, дополнительные коды чисел А1 = 0,11010 и А2 = -0,11010 будут иметь вид [А1] доп = 0,11010; [А2] доп = 100101 + 000001 = 100110.
Отрицательное число = Инвертирование до последней правой единицы.