Макроекономіка Радіонова

• поясненням переходу від хибних цінових сигналів до зростання пропозиції праці через явище «міжчасового заміщення пропозиції праці»*.

Модель бізнес-циклу Фрідмена—Лукаса містить низку так званих запитань без відповідей. Зокрема, модель не дає відповіді на такі питання:

♦наскільки обґрунтованим є пояснення піднесень і спадів постійними помилковими оцінками економічних суб’єктів щодо зміни рівня цін;

♦як узгодити теорію «міжчасового заміщення пропозиції праці» з фактами незначної реакції заміщення працею вільного часу при зростанні доходів;

♦як співвіднести контрциклічний (падіння за економічного піднесення та зростання в разі спаду) рух прибутку фірм, що випливає

зтвердження про хибну оцінку, з реальними фактами проциклічного(зростання за піднесення та падінняза спаду) рухуприбутків;

♦в який спосіб надлишкові інвестиції періоду піднесення повертаються до нормального рівня, не спричиняючи загального економічного спаду після того, як з’ясовується хибність реакції суб’єктів на цінові сигнали?

На неможливість дати відповіді на сформульовані питання у

межах базової моделі Фрідмена—Лукаса звертали увагу різні дослідники, наприклад, Р. Гаррісон та Г. Манків1.

Відповіді на деякі з цих запитань дала монетарна модель нерів-

новаги Варбуртона—Єгера.

Припущення моделі:

•економіка представлена трьома взаємодіючими ринками: грошовим, товарним та праці;

•існує жорсткість (нееластичність) товарних цін і заробітних плат;

•обсяги попиту та пропозиції на товарному ринку реагують на зміну пропозиції грошей швидше, ніж ціни;

•має місце відносно більша гнучкість цін товарного ринку порівняно з цінами ринку ресурсів (праці).

Зміст моделі

Зміст моделі розкривається через логіку монетарного імпульсу, який розпочинається з неочікуваної зміни грошової пропозиції.

* Міжчасове заміщення праці вже розглядалось у цьому посібнику при поясненні моделі Лукаса—Реппінга в підрозд. 1.1.1.

1 Garrison R. Net Austrian theory of the business cycle in the light of modern economics (1989); Mankiw G. A Quick refresher course in macroeconomics (1990).

151

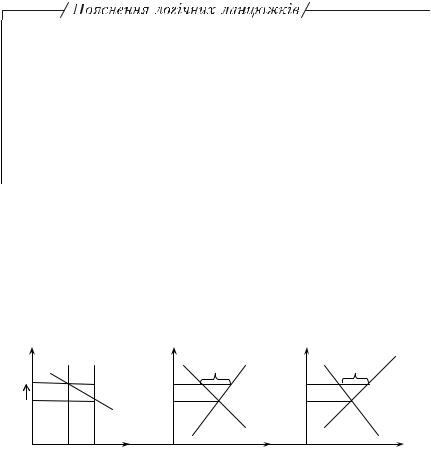
Умоделі передбачена «асиметрія» передачі монетарного імпульсу за піднесення та спаду. Це ілюструють два логічні ланцюжки:

монетарний імпульс за економічного піднесення:

M unexS ↑→ Y D ↑→ Inv ↓→ L ↑→ Y S ↑ ;

монетарний імпульс за економічного спаду:

M unexS ↓→ C ↓, LS ↑→ Y D <Y S → Y S ↓,

де Inv — товарні запаси; С — споживчі витрати.

X Для економічного піднесення передбачається, що збільшення пропозиції грошей створює додатковий попит, який спричиняє скорочення товарних запасів і забезпечує повне використання виробничих ресурсів (праці) з відповідним зростанням продукту.

X При спаді скорочення пропозиції грошей спричиняє змен-

шення схильності до закупівель і споживання та збільшення схильності до продажу всіх товарів включно з ресурсом праці. Тож створюється надлишок пропозиції над попитом і відбувається скорочення виробництва.

Явище нерівноваги пов’язується в аналізованій моделі зі зміною поведінкових чинників — схильностей до споживання та пропонування товарів і праці — саме у фазі економічного спаду. Ця зміна має у своїй основі невідповідність фактичних та очікуваних цін.

Механізм нерівноваги при економічному спаді ілюструє система графіків на рис. 2.7.

Рис. 2.7

152

Рівняння (2.26) відображає те, що внаслідок зменшення грошової пропозиції за незмінного попиту виникають розриви між пропозицією та попитом на товарному і ресурсному (праці) ринках.

Модель Варбуртона—Єгера передбачає виникнення крім уже розглянутої нерівноваги при спаді особливої нерівноваги так званого другого порядку. Вона формується в процесі руху економіки від нерівноважного стану, спричиненого монетарним імпульсом, до стану нової рівноваги. Отже, їй передує ситуація, зображена

системою графіків на рис. 2.7.

Нерівновага «другого порядку» пов’язана з різною швидкістю пристосування цін до монетарного імпульсу. Ідеться про те, що товарні ціни пристосовуються до змін пропозиції грошей швидше, ніж ресурсні. Це припущення можна формалізувати в такий спосіб:

∂∂MP > ∂∂WM .

Якщо припустити, що ціни товарного ринку повністю «поглинають» надлишок попиту на гроші, а рівень зарплат відстає у своєму реагуванні, то матимемо ситуацію, коли лише на двох (з трьох) взаємозв’язаних ринках спостерігається рівновага. Тому ситуацію загальної нерівноваги можна описати такою системою залежностей:

M S = M D ;

Y S =Y D ;

LS > LD .

Нерівність LS >LD відображає розбалансування ринку праці, відповідно, факт існування недобровільного безробіття. Воно співіснує з рівновагою на грошовому і товарному ринках.

Загалом монетарне пояснення нерівноваги за моделлю Варбур- тона—Єгера можна звести до таких положень:

•нерівновага є результатом сприйняття економікою монетарного імпульсу — зміни пропозиції грошей;

•важливим елементом передавального механізму (трансмісії) монетарного імпульсу є зміна схильностей суб’єктів економіки до споживання та праці;

•зміна схильностей формується внаслідок невідповідності фактичних та очікуваних цін і спричиняє розрив між пропозицією та попитом на товарному і ресурсному (праці) ринках;

154

• можливі два вияви загальної нерівноваги: той, що пов’я- заний з початковим розгортанням монетарного імпульсу (нерівновага «першого порядку»), і той, що виявляє різну еластичність цін товарного та ресурсного (праці) ринків на зміну пропозиції грошей (нерівновага «другого порядку»).

♦зростання ставки відсотка та наступне «витіснення» частини приватних витрат*;

♦прискорення інфляційного зростання цін;

♦погіршання сальдо торгового та платіжного балансу;

♦уповільнення темпів економічного зростання.

Зазначені наслідки фінансового регулювання були предметом багатьох теоретичних та емпіричних досліджень1.

Модель Бліндера—Солоу належить саме до групи моделей, в яких нерівновага асоціюється з нестабільністю та нестійкістю економічної системи. Вона була однією з перших теоретичних конструкцій, що пояснювала нестійкість як наслідок фінансового регулювання економіки. При цьому в ній ідеться про нестійкість, пов’язану лише з певним способом фінансування дефіциту державного бюджету.

Умови моделі:

•можливість альтернативного фінансування додаткових державних витрат (бюджетного розриву) через грошову емісію та боргові зобов’язання держави;

•визнання дії ефекту багатства при борговому фінансуванні державних витрат;

•урахування трьох складників багатства, відповідно, трьох форм активів: фізичного капіталу, грошей та цінних паперів;

•використання аналітичного апарату моделі IS-LM для пояснення станів стійкої та нестійкої рівноваги.

* Докладно про це йтиметься в підрозд. 4.2 при поясненні наслідків стабілізаційної фінансової політики.

1 Див., наприклад: Blanchard O., Perotti R. An empirical characterization of the dynamic effect of changes in government spending and Taxes on output // Quarterly Journal of Economics. — 2002. — Vol. 117. — P. 129—168; Ganelly G. Useful government spending, direct crowding — out and fiscal policy interdependence // Journal of International Money and Finance. — 2003. — Vol. 22. — P. 87—103.

155

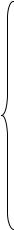
Зміст моделі

Зміст моделі розкриває така система рівнянь:

T= T (Y , B) — функція чистих (без державних трансфертів)

++

кова вартість боргових зобов’язань держави; B — щорічні відсоткові платежі за борговими зобов’язаннями держави; K — запас

фізичного капіталу.

Особлива роль у розглянутій системі покладається на рівняння (2.31) бюджетного обмеження. Воно робить модель динамічною в тому сенсі, що відображає процес переходу від одного стану рівноваги до іншого через зміни запасу грошей та запасу державних цінних паперів.

Нестабільність економічної системи в моделі Бліндера—Солоу має два рівні вияву.

Перший рівень пов’язаний з явищем зростання ставки відсотка під впливом фінансового імпульсу та реакцією на нього продукту (доходу).

За логікою моделі IS-LM, що використана у моделі Бліндера— Солоу, зростання ставки відсотка є наслідком збільшення попиту на гроші. Якщо зростання ставки відсотка не нейтралізовано, то наслідком може стати витіснення приватних витрат та відносне зменшення мультиплікативного ефекту.

156

Входження економіки у стан нестабільності визначається способом фінансування бюджетного розриву. Більша ймовірність незростання ставки відсотка, а отже, перебування економіки у стійкому стані, пов’язана з грошовим ( ∆M ) фінансуванням бюджетного розриву. За такого способу фінансування ставка відсотка може повернутися до попереднього рівня. Натомість при борговому фінансуванні повернення ставки відсотка не передбачається. Саме при борговому фінансуванні економічна система втрачає стійкість, увійшовши в стан так званої нестабільності першого рівня.

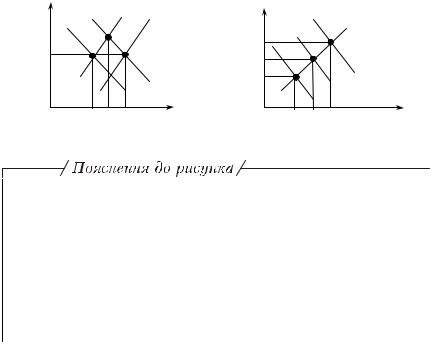
Наслідки грошового фінансування надлишкових державних витрат (бюджетного розриву) зображені з використанням інструментарію моделі IS-LM на графіку 1, а боргового — на графіку 2 (рис. 2.8).

Рис. 2.8

X На обох графіках перехід від точки 1 до точки 2 зображує початковий результат фінансового стимулювання економіки, який спричиняє дефіцит бюджету (бюджетний розрив).

X Точка 3 на графіку 1 ілюструє наслідки емісійного фінансування бюджетного розриву та означає досягнення стабільності в тому сенсі, що ставка відсотка повертається до попереднього рівня.

X Точка 3 на графіку 2 ілюструє наслідки боргового фінансування та входження економіки у стан нестабільності (нестійкої рівноваги) першого рівня через зростання ставки відсотка.

Другий рівень нестабільності економічної системи при борговому фінансуванні пояснюється дією ефекту багатства. Автори моделі розуміють державні облігації як форму чистого

157

багатства, тому володіння ними суттєво впливає на поведінку економічних суб’єктів*.

Саме включення ефекту багатства в логіку пояснення кінцевих результатів фінансового регулювання допомагає обґрунтувати втрату економічною системою стабільності при борговому фінансуванні.

Ефект багатства має два наслідки, що важливі для оцінки кінцевих результатів фінансового регулювання:

•збільшення споживання;

•зростання попиту на гроші.

На графіку моделі IS-LM два наслідки ефекту багатства відображаються, відповідно, зсувом праворуч функції IS через зростання споживання та ліворуч функції LM — через зростання попиту на гроші.

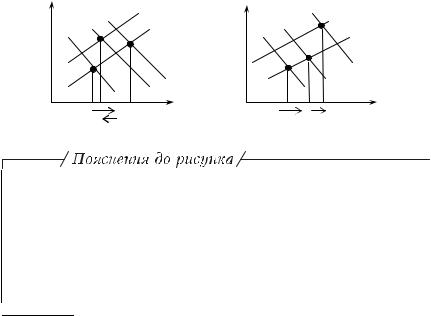
Наслідки ефекту багатства зображені на рис. 2.9 (графіки 1 і 2). Другий рівень нестабільності економічної системи ілюстро-

вано на графіку 1.

Рис. 2.9

X На графіку 1 показано, що боргове фінансування бюджетного розриву передбачає часткове нівелювання (витіснення) початкового позитивного результату, отриманого у вигляді збільшення продукту. Причиною витіснення є менший (порівняно зі зміною попиту на гроші) приріст споживання та, відповідно, менший правобічний зсув IS. Позитивний результат фінансового імпульсу витіснятиметься доти, доки зберігатиметься дефіцит бюджету.

* Дуже поширеним є протилежний погляд на облігації як на цінні папери, що не змінюють багатства, оскільки їх випуск передбачає зростання податкового навантаження на економічних суб’єктів у майбутньому. Такий альтернативний підхід, зокрема, представлений теоремою еквівалентності Рікардо—Барро, яка буде розглянута в підрозд. 4.2.

158

X На графіку 2 ілюстровано відсутність витіснення позитивного результату фінансового імпульсу при борговому фінансуванні, оскільки зміна споживчих витрат і відповідний зсув IS є більшими, ніж зміна попиту на гроші і відповідний зсув LM.

Із системи рівнянь моделі виводяться умови, за яких витіснення позитивного результату фінансового імпульсу внаслідок дії ефекту багатства не відбувається. Отже, умови стабільності системи такі:

перша умова стабільності: dYdB >1−TT′ ′ ; друга умова стабільності: IK +CW < 0,

де T ′ = dTdY — зміна податкової ставки за зміною доходу, або гра-

нична схильність до оподаткування; IK = − dKdI — еластичність

інвестицій за обсягом капіталу; CW = dWdC

вання за обсягом багатства. Порушення умов стабільності має означати входження економіки у стан нестабільності, або нерівноваги.

Пояснення нерівностей (умов стабільності економічної системи).

• Перша умова стабільності виводиться як часткова похідна функції бюджетного обмеження, поданого рівнянням

∆M + ∆rB = G + B −TW (Y + B) ,

де TW — податкова ставка за всім обсягом багатства.

Тут вираз [ TW (Y + B) ] відображає те, що державні облігації

( B ) так само, як і дохід (Y ), формують багатство економічних суб’єктів. Стійка рівновага в довгому періоді (long-run steadystate solution) допускає незмінність як грошової пропозиції, так і

боргових зобов’язань: ∆M = ∆rB = 0 . За такої умови рівняння бюджетного обмеження перетворюється на G + B =TW (Y + B) . Звідси: dYdB = 1−TT′ ′ .

159

стабільною, тобто економіка не повертається до рівноваги, яка

передувала фінансуванню дефіциту борговими зобов’язаннями.

зрости, але цього приросту буде недостатньо для подолання бюджетного розриву.

• Друга умова стабільності враховує зміну запасу фізичного

капіталу і пов’язана з функцією ∆K = I(r, K ) , яка виводиться з

− −

модифікованої функції попиту на інвестиції I = I(r, K) . При цьо-

− −

му враховується, що реальна ставка відсотка, яка визначає попит на інвестиції, залежить від усіх елементів суспільного багатства:

r = r(M , B, K) .

Передбачається подвійний результат від збільшення запасу капіталу щодо сукупного попиту і доходу:

через зростання споживання внаслідок дії ефекту багатства, елементом якого є фізичний капітал;

через зменшення інвестицій, зв’язок між якими та запасом капіталу є зворотним.

Отже, загальний вплив змін капіталу на сукупний попит ( dY )

розкладається на CW dK та IK dK . Отже, загальний результат зміни запасу капіталу на одну одиницю можна оцінити як IK +CW . Умова IK +CW < 0 у підсумку відображає те, що зміна продукту за

Останнє означає, що прирісткапіталу випереджає приріст доходу.

Вираз dYdB з першої умови стабільності економічної системи

за моделлю Бліндера—Солоу фактично є мультиплікатором зміни продукту (доходу) за зміни відсоткових виплат за борговими зобов’язаннями.

З формули dYdB = 1−TT′ ′ випливає, що цей мультиплікатор буде більшим від 1, якщо гранична ставка оподаткування не пере-

160