13.11. Перестраиваемый универсальный фильтр

Из вышеизложенного следует, что пере­даточная функция произвольного фильтра второго порядка в общем виде может быть представлена в следующем виде:

Передаточные функции описанных выше фильтров различного вида могут быть по­лучены из формулы (13.41) при следующих значениях параметров:

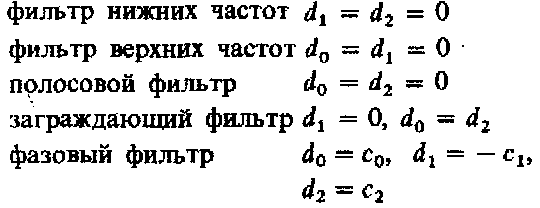
Коэффициенты числителя могут иметь произвольные знаки, тогда как коэффи­циенты знаменателя в любом случае дол­жны быть положительными, что следует из условий устойчивости схемы. Добротность полюсов определяется коэффициентами знаменателя:

В предыдущих разделах для каждого из рассмотренных фильтров приводилась специальная, как можно более простая, прин­ципиальная схема. Иногда, однако, возни­кает необходимость построения такой еди­ной схемы фильтра, с помощью которой была бы возможна реализация всех ранее описанных фильтров, а также любых дру­гих видов фильтров, соответствующих со­отношению (13.41), с произвольными коэф­фициентами числителя. Этим требованиям удовлетворяет схема, приведенная на рис. 13.36. Ее основное достоинство со­стоит в том, что каждый коэффициент передаточной функции может быть устано­влен независимо от других. Кроме того, для настройки каждого коэффициента используется только один элемент схемы. Передаточная функция схемы имеет сле­дующий вид:

Здесь ₀-нормированная частота, а =RC-постоянная времени обоих инте­граторов. Коэффициенты k_i и l_i опреде­ляются соотношениями сопротивлений и поэтому всегда положительны. При необходимости изменения знака коэффициен­тов числителя следует применить дополнительный усилитель для инвертирования входного напряжения фильтра и добавить соответствующий резистор.

Рис. 13.36. Универсальный фильтр второго порядка с независимо настраиваемыми коэффициента­ми.

Для реализации фильтров более высо­кого порядка можно увеличить число соответствующих интеграторов в схеме. Од­нако для этой цели гораздо удобнее использовать последовательное соединение универсальных фильтров второго порядка.

Рассмотрим пример числового расчета схемы фильтра. Необходимо получить характеристики фазового фильтра второго порядка с максимальной шириной по­лосы группового времени задержки, рав­ной на низких частотах 1 мс. Из табл. 13.9 получаем а₁ = 1,6278, b₁ = 0,8832 и Т_gr0 = 0,5181. На основании формулы (13.9а) рассчитаем частоту среза

Выберем  = 1 мс и приравняем коэффи­циенты выражений (13.43) и (13.38) для _o = 2f_g=3,26кГц; запишем расчетные соотношения:

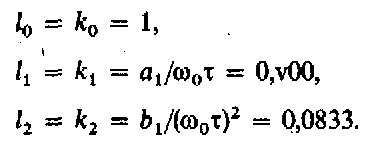
Столь малое значение коэффициента l₂ не­удобно при реализации фильтра. Его зна­чение должно увеличиваться при уменьше­нии  в большей степени, чем значения других коэффициентов. Поэтому выберем  = 0,3 мс. В результате получим

В некоторых случаях желательно, чтобы резонансную частоту, добротность и коэффициент передачи на резонансной частоте в селективном фильтре можно бы­ло настраивать независимо друг от друга. Как показывает сравнение выражений (13.43) и (13.24), для установки заданного значения добротности без изменения коэф­фициента передачи фильтра необходимо одновременно перестраивать коэффи­циенты l₁ и k₁. На рис. 13.37 приведена схема фильтра, удовлетворяющая этим требованиям.

Интересной особенностью схемы является то, что она в зависимости от то­го, какой выход используется, работает одновременно как селективный, загра­ждающий, фазовый фильтр и фильтр верх­них частот. Для расчета характеристик фильтра запишем соотношения между на­пряжениями схемы:

Рис. 13.37. Универсальный фильтр второго порядка с независимо настраиваемыми характеристика­ми.

Исключая, где это необходимо, из уравне­ний соответствующие значения выходных напряжений, получим выражения для коэф­фициентов передачи для различных выхо­дов:

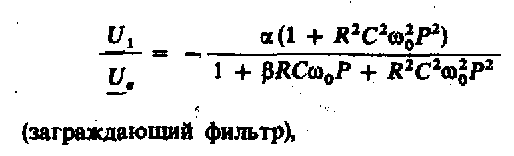
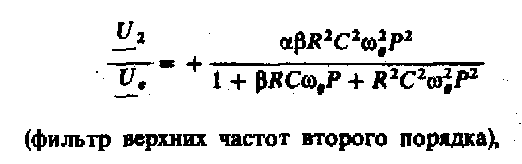
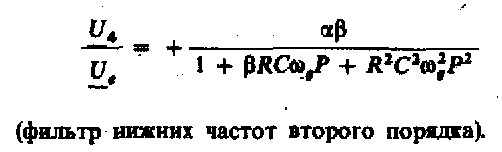
Приравнивая коэффициенты в выражениях (13.37), (13.12), (13.24) и (13.11), найдем следующие характеристики фильтров:

Отсюда видно, что в случае использования схемы в качестве селективного или заграждающего фильтра резонансная частота, коэффициент передачи и добротность мо­гут быть установлены независимо друг от друга. Из приведенных формул следует, что резонансная частота определяется про­изведением RС. Поскольку эта величина не входит в выражения для A и Q, можно на­страивать резонансную частоту фильтра, не изменяя А и Q. Последние два параме­тра фильтра могут быть независимо уста­новлены с помощью сопротивлении R₁/ и R₂/.

Фильтр нижних частот: Фильтр верх­них частот:

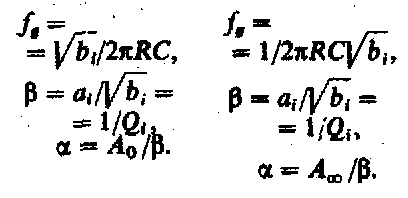
Из формул для расчета фильтров ниж­них и верхних частот следует, что коэффициент  определяет тип фильтра, RС-ча­стоту среза и -коэффициент передачи. При заданном типе фильтра ( = const) ча­стота среза и коэффициент передачи мо­гут быть изменены независимо друг от друга.

Коэффициент  является обратной ве­личиной добротности полюсов Q_i,значе­ния которой приведены в табл. 13.6. Она совпадает с добротностью Q селективного выхода фильтра. Поэтому формально вве­денную добротность полюсов, равную Q_i = /а_i, можно рассматривать как до­бротность соответствующего селективного фильтра с тем же полиномом знамена­теля.

Для низких частот расчетное значение сопротивления R будет достаточно велико. Поэтому предпочтительнее заменять его делителем напряжения в виде цепочки из резистора постоянного сопротивления и дополнительного потенциометра. Такой же прием можно применить и для резисто­ров R₁ и R₂.

Если желательно изменять параметры фильтра с помощью напряжении, то только что рассмотренный делитель напряже­ния можно заменить аналоговой схемой умножения, на второй вход которой по­дается управляющее напряжение (рис. 13.38). Эквивалентное сопротивление такой схемы равно

Рис. 13.38. Схема умножения для регулировки сопротивления.

Здесь U_упр-управляющее напряжение. Заменив такой схемой оба частотно-зави­симых переменных сопротивления R, полу­чим следующую зависимости резонансной частоты от управляющего сигнала:

Таким образом, резонансная частота про­порциональна управляющему напряжению.