1. Фильтр с критическим затуха­нием: 2-фильтр Бесселя:

3. Фильтр Баттерворта; 4 фильтр Чебышева с неравномерностью 3дБ.

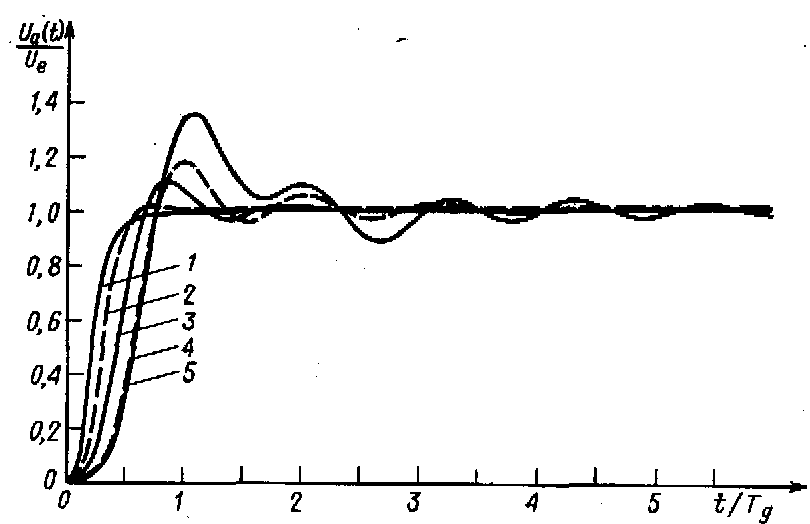
Рис. 13.3. Переходные характеристики фильтров нижних частот четвертого порядка при ступенча­том входном сигнале.

1-фильтр с критическим затуханием; 2-фильтр Бесселя; 3-фильтр Баттерворта; 4-фильтр Чебышева с неравномерностью 0,5 дБ; 5 -фильтр Чебышева с неравномерностью 3 дБ.

Характеристика фильтра Чебышева спадает более круто за частотой среза. В полосе пропускания она, однако, не мо­нотонна, а имеет волнообразный характер с постоянной амплитудой. При заданном порядке фильтра более резкому спаду амплитудно-частотной характеристики за час­тотой среза соответствует большая нерав­номерность в полосе пропускания. Колеба­ния переходного процесса при ступенчатом входном воздействии сильнее, чем у филь­тра Баттерворта.

Фильтр Бесселя обладает оптимальной переходной характеристикой. Причиной этого является пропорциональность фазо­вого сдвига выходного сигнала фильтра частоте входного сигнала, В общем случае спад амплитудной характеристики фильтра Бесселя оказывается более пологим по сравнению с фильтрами Чебышева и Бат­терворта.

На рис. 13.2 показаны амплитудно-частотные характеристики четырех рассмот­ренных фильтров нижних частот четверто­го и десятого порядка. Можно заметить, что характеристика фильтра Чебышева имеет наиболее крутой спад для частот входного сигнала, превышающих частоту среза, но заметную неравномерность в по­лосе пропускания. При увеличении равно­мерности амплитудной характеристики фильтр Чебышева переходит в фильтр Баттерворта [13.1]. Переходные характери­стики этих фильтров имеют большую ам­плитуду колебаний при ступенчатом вход­ном сигнале. Это хорошо видно из рис. 13.3. Переходный процесс для филь­тра Бесселя практически не имеет колеба­ний. Несмотря па менее удовлетвори­тельные амплитудно-частотные характери­стики фильтра Бесселя, он обеспечивает весьма высокое качество отработки ступен­чатого входного сигнала. Пассивный RС- фильтр нижних частот не имеет перере­гулирования, однако обладает значительно худшей амплитудно-частотной характери­стикой по сравнению с фильтром Бесселя и несколько уступает ему в отношении ка­чества отработки входною ступенчатого сигнала.

В табл. 13.1 приведены значения вре­мени нарастания и задержки выходного сигнала, а также относительного перерегу­лирования для фильтров нижних частот различного типа. Время нарастания опре­деляет интервал, за который выходной сиг­нал возрастает от 10 до 90% своего устано­вившегося значения. Время задержки со­ответствует интервалу, в течение которого выходной сигнал достигает 50% установив­шегося значения.

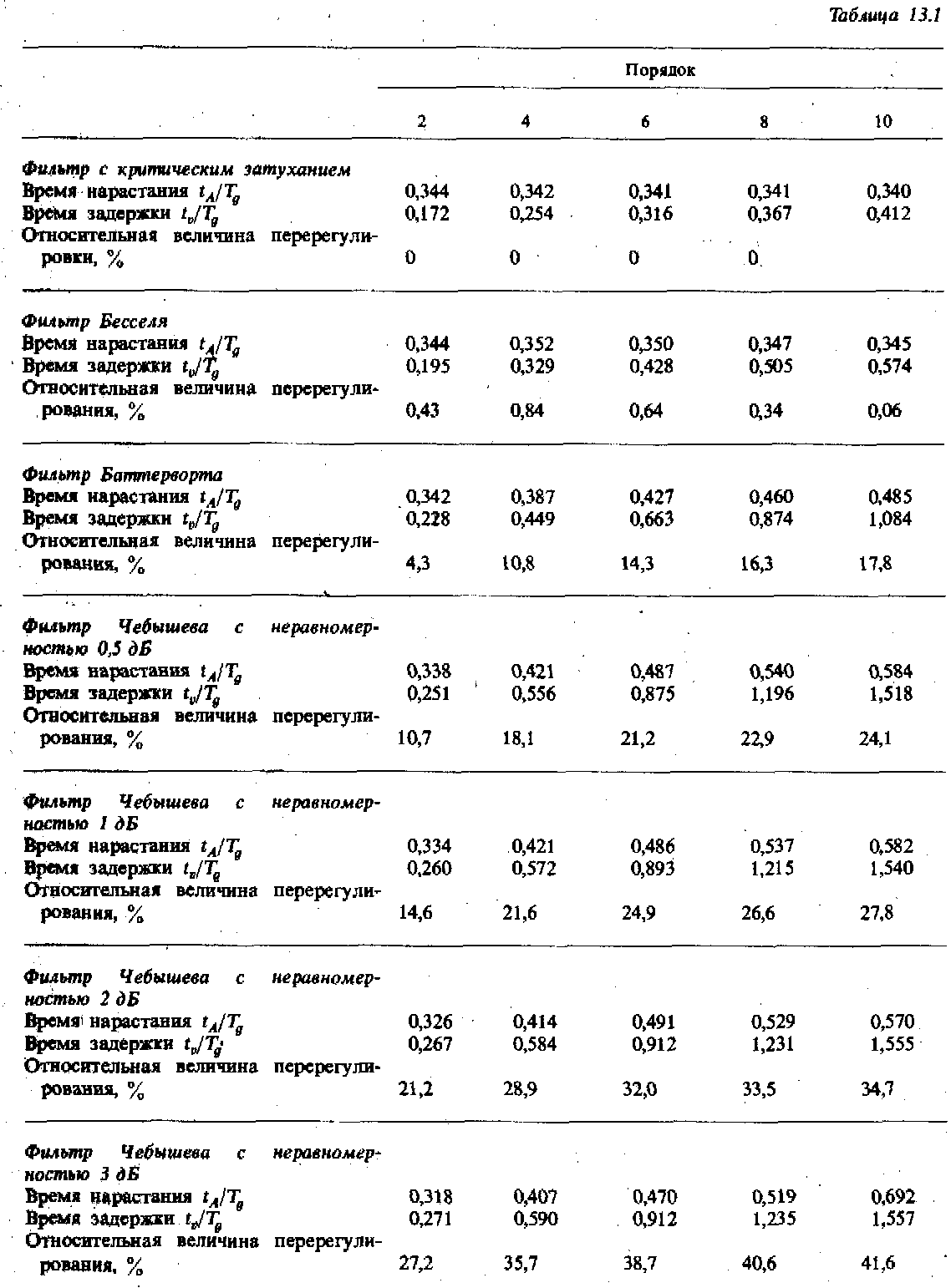
Из таблицы следует, что время нараста­ния выходного сигнала мало зависит от порядка и типа фильтра и составляет при­близительно 1/3fg (как отмечалось в разд. 2.1.3). Если учесть время задержки и относительное перерегулирование, то су­щественными преимуществам перед дру­гими обладает фильтр Бесселя. Увеличение порядка этого фильтра, начиная с четвер­того, приводит к затуханию колебаний переходного процесса.

Ниже будет показано, что с помощью одной и той же схемы можно получить ха­рактеристики фильтра любого типа опре­деленного порядка, изменяя лишь номи­налы соответствующих резисторов и кон­денсаторов. Для того чтобы рассчитать схему конкретного фильтра, следует знать частотные характеристики каждого филь­тра при заданном его порядке. Поэтому рассмотрим их в следующем разделе.

13.1.1. ФИЛЬТР БАТТЕРВОРТА

Из формулы (13.3) следует, что модуль коэффициента передачи фильтра n-го по­рядка может быть описан следующим вы­ражением:

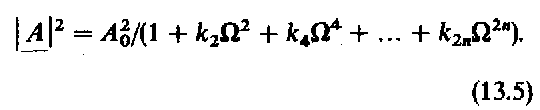
Нечетные степени в выражении (13.5) от­сутствуют, поскольку А² является чет­ной функцией. Для фильтра Баттерворта график функции А² должен быть по воз­можности горизонтальным при частотах входного сигнала, меньших частоты среза. Поскольку в этой области  < 1, для вы­полнения такого требования необходимо, чтобы функция А² зависела только от старшей степени . Это связано с тем, что при  < 1 младшие степени вносят большой вклад в знаменатель выражения (13.5) и, следовательно, приводят к существенному уменьшению коэффициента пере­дачи фильтра. Итак, запишем

Коэффициент k_2n определяется из условия нормировки, которое связано с необходи­мостью обеспечения снижения коэффи­циента передачи фильтра на 3 дБ при час­тоте  = 1, т.е.

Отсюда следует, что k_2n == 1. Таким обра­зом, выражение для квадрата коэффициен­та передачи низкочастотного фильтра Бат­терворта n-го порядка имеет следующий вид:

В это выражение входит только старшая степень ; в связи с этим фильтр Баттер­ворта нижних частот называют степенным фильтром нижних частот.

Для практической реализации фильтра Баттерворта необходимо разработать схе­му, квадрат коэффициента передачи кото­рой удовлетворяет соотношению (13.6). Обычно при анализе электронных схем применяют не квадрат коэффициента пере­дачи А², а. непосредственно сам комп­лексный коэффициент А. Для того чтобы было легче рассчитывать схему фильтра, необходимо знать соответствующий выра­жению (13.6) комплексный коэффициент- передачи. Для этого приравняем коэффи­циенты выражений (13.3) и (13.6). В резуль­тате найдем коэффициенты c₁, ...с_n. По­лученный таким образом знаменатель вы­ражения (13.3) является полиномом Баттер­ворта (табл. 13.2).

В работе [13.2] показано, что полюсы передаточной функции фильтра Баттервор­та могут быть получены в замкнутой фор­ме. Объединяя комплексно- сопряженные полюсы, можно записать аналитические выражения для коэффициентов аi и bi, в передаточной функции (13.4):

для четных n

для нечетных n

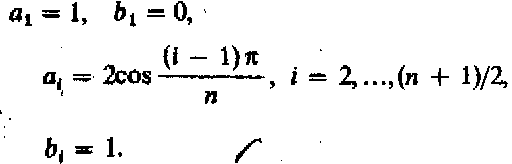
Коэффициенты Баттерворта для полино­мов до 10 порядка приведены в табл. 13.6.

Известно, что фильтр Баттерворта пер­вого порядка представляет собой пас­сивный фильтр нижних частот с передаточ­ной функцией (13.1). Корни полиномов Баттерворта более высокого порядка являются комплексно-сопряженными. В связи с этим они не могут быть реализо­ваны с немощью пассивных RС- цепей, со­ответствующих действительным значениям корпев знаменателя передаточной функции. Поэтому для построения фильтров Баттерворта следует применять пассивные LRC-схемы или активные RС- цепи. Час­тотные зависимости коэффициентов пере­дачи фильтров Баттерворта для различных значений n приведены на рис. 13.4.

13.1.2. ФИЛЬТР ЧЕБЫШЕВА

Коэффициент передачи фильтра Чебышева для низких частот равен а(,, однако в области частот, меньших частоты среза, его амплитудно-частотная характеристика имеет волнообразный характер, причем амплитуда этих колебаний определяется параметрами фильтра. Полиномы, обла­дающие таким свойством, называются по­линомами Чебышева:

-

коэффициенты которых указаны в табл. 13.3.

В области 0  х  1 функция Т(х) колеблется между 0 и 1, а при х > 1 моно­тонно возрастает. Выражение для | A |² фильтра нижних частот на основе полино­мов Чебышева имеет следующий вид:

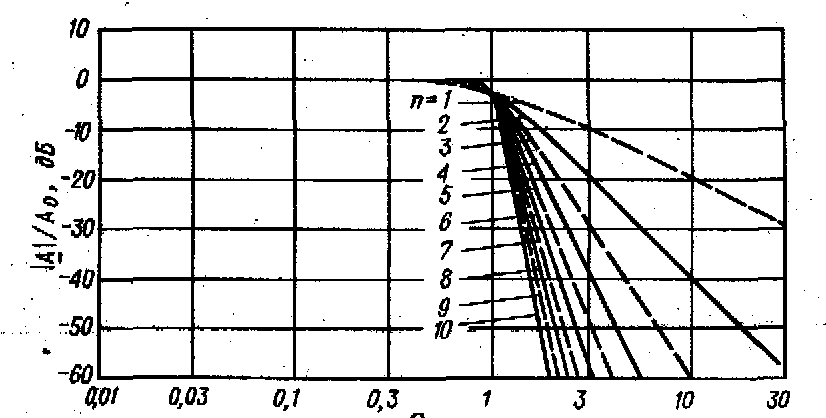
Рис. 13.4. Частотные ха­рактеристики коэффи­циентов передачи филь­тров Баттерворта.

Постоянный коэффициент k выбирается так, чтобы при х = 0 выполнялось условие A² = А²₀. Отсюда следует, что k = 1 для полиномов нечетного порядка и k = 1 + ² для четных n. Множитель  опреде­ляет степень неравномерности характери­стики фильтра:

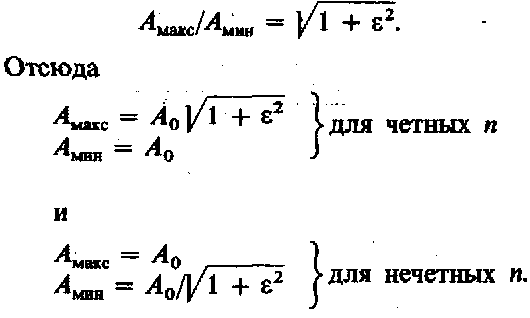
В табл. 13.4 приведены параметры фильт­ра Чебышева для различной степени не­равномерности. В принципе, задав значение коэффициента передачи, можно полу­чить выражение для комплексного коэффи­циента передачи и из него найти коэффи­циенты факторизованной формы. Однако удобнее вычислять полюсы передаточной функции фильтра непосредственно [13.3], используя выражения для коэффициентов фильтра Баттерворта. Объединяя ком­плексно-сопряженные полюсы передаточ­ной функции,

запишем для коэффициентов аi и bi (13.4) следующие выражения:

для четных значений n

В приведенных выражениях  = 1/n-Arsh 1/.

Подставив в выражение (13.4) коэффи­циенты а`i и b`i вместо аi и bi получим пере­даточную функцию фильтра Чебышева нижних частот, в которой Р нормировано не относительно частоты wg (соответствую­щей снижению коэффициента передачи на 3 дБ), а относительно частоты wc, при ко­торой коэффициент передачи фильтра в последний раз принимает значение Амин.

Для того чтобы было удобнее сравни­вать характеристики фильтров различного типа, следует нормировать Р относительно частоты wg. Для этого заменим Р на Р и выберем постоянную нормирования я так, чтобы коэффициент передачи для Р = j имел значение . Тогда ква­дратный трехчлен в знаменателе примет вид

Из сопоставления полученного выражения с (13.4) следует, что

Коэффициенты аi и bi передаточных функций фильтров до 10-го порядка для значений неравномерности амплитудно-частотных характеристик, равных 0,5, 1, 2 и 3 дБ, приведены в табл. 13.6. Амплитудно-частотные характеристики коэффициен­та передачи для значений неравномерности 0,5 н 3 дБ приведены на рис. 13.5.

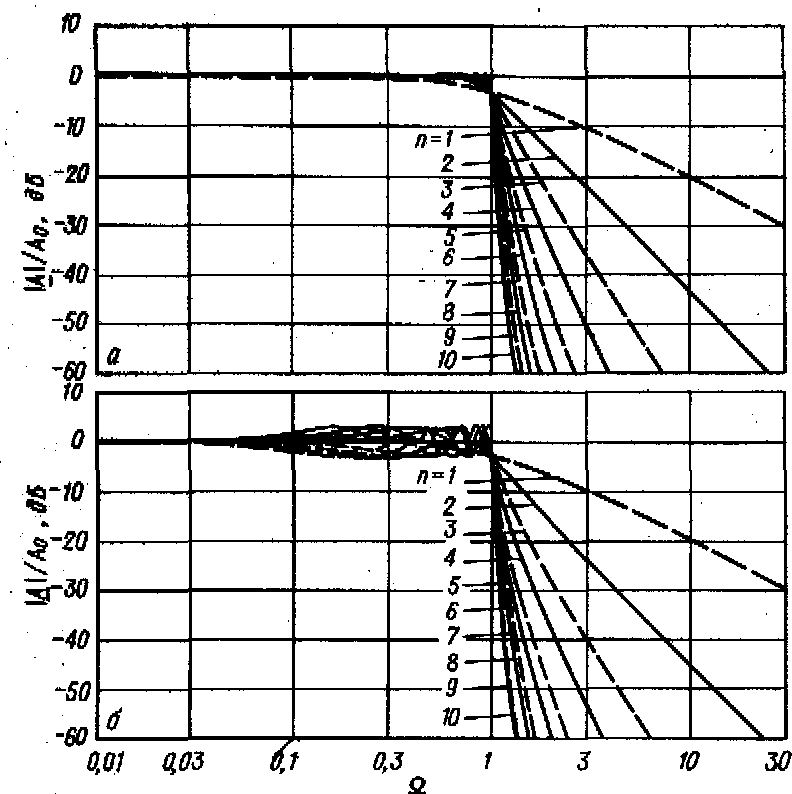
Рис. 13.5. Амплитудно-частотные характеристи­ки коэффициентов пере­дачи фильтров Чебы­шева.

а- неравномерность 0.5 дБ; б- неравномерность 3 дБ.

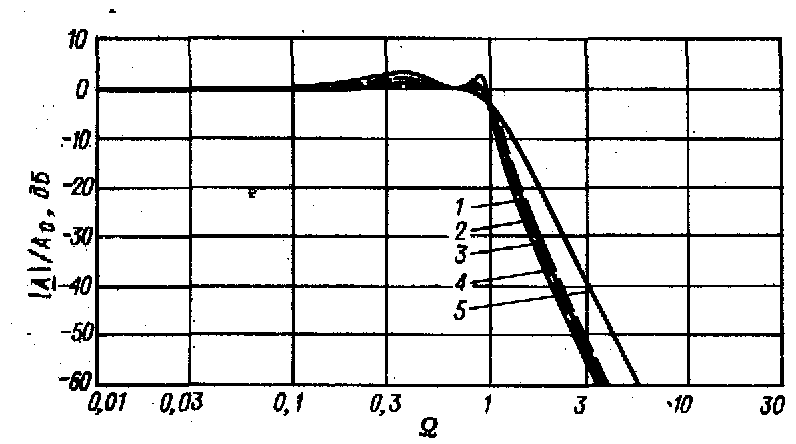
Рис. 13.6. Амплитудно-частотные характеристики фильтров Чебышева четвер­того порядка.

Неравномерность:

кривая 1-3 дБ: кривая 2-2дБ; кривая 3-1 дБ; кривая 4-0,5 дБ;

5-фильтр Баттерворта четвертого порядка (для сравнения).

На рис. 13.6 для сравнения представлены амплитудно-частотные характеристики фильт­ров Чебышева четвертого порядка для раз­личных значений неравномерности. Можно заметить, что характеристики в области  > 1 очень мало отличаются. Для филь­тров более высокого порядка они будут отличаться еще меньше. По сравнению с приведенной на том же рисунке амплитудно-частотной характеристикой фильтра Баттерворта амплитудно-частотная харак­теристика фильтра Чебышева с неравно­мерностью 0,5 дБ имеет более крутой спад.

Переход от полосы прозрачности к по­лосе заграждения фильтра нижних частот может быть сделан еще более резким. Кро­ме того, можно так выбрать параметры схемы, чтобы и в области заграждения фильтра нижних частот получить задан­ную неравномерность амплитудно-частотной характеристики. Такие фильтры на­зываются фильтрами Кауэра. Передаточ­ная функция фильтра Кауэра отличается от передаточных функций рассмотренных ранее фильтров тем, что ее числитель вме­сто постоянного коэффициента A₀ содер­жит полином. Эти фильтры не могут быть реализованы с помощью достаточно про­стых схем, которые приведены ниже в разд. 13.4. В разд. 13.11 рассмотрена схе­ма универсального фильтра, с помощью которого представляется возможным обра­зовать произвольные полиномы числителя передаточной функции фильтра. Коэффи­циенты полиномов Кауэра содержатся в работе [13.4].

13.1.3. ФИЛЬТРЫ БЕССЕЛЯ

Фильтры Баттерворта и Чебышева ха­рактеризуются большими колебаниями переходных процессов. Идеальными в от­ношении обработки ступенчатого входного сигнала являются фильтры с частотно-не­зависимым групповым временем задержки, т. е. с фазовым сдвигом, пропорцио­нальным частоте. Этим свойством обла­дают фильтры Бесселя, иногда называемые фильтрами Томсона. Параметры фильтра рассчитываются так, чтобы групповое вре­мя задержки в области частот, превышаю­щих  = 1, как можно меньше зависело от частоты . Для этого используют аппрок­симацию Баттерворта для группового времени задержки.

Из формулы (13.4) следует, что коэффи­циент передачи фильтра нижних частот второго порядка для Р = j может быть представлен следующим образом:

Отсюда видно, что фазовый сдвиг в зави­симости от частоты входного сигнала ра­вен

Групповое время задержки определяется как

Для упрощения дальнейших выкладок введем нормированное групповое время за­держки:

где Тg- обратная величина частоты среза фильтра. Запишем теперь

и, учитывая формулу (13.8), получим

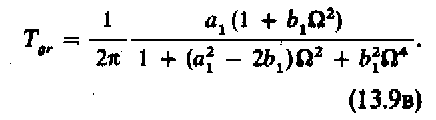
Для того чтобы аппроксимировать группо­вое время задержки в смысле Баттерворта, воспользуемся тем, что для  << 1 справед­ливо следующее соотношение:

Это выражение не будет зависеть от , ес­ли коэффициенты при ² в числителе и знаменателе совпадают. Для этого дол­жно удовлетворяться следующее соотно­шение:

Второе соотношение может быть выведено из условия нормировки | А |² = 1/2 для ча­стоты =1:

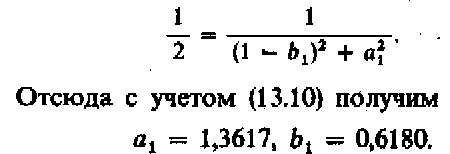
Вычисление коэффициентов для полиномов более высокого порядка представляет до­статочно трудоемкую задачу, связанную с решением систем нелинейных уравнений.

Однако можно аналитически вычислить коэффициенты с, полинома знаменателя передаточной функции (13.3) с использова­нием рекуррентных соотношений [13.5]:

Полученные коэффициенты определяют полиномы Бесселя, вид которых до четвер­того порядка показан в табл. 13.5

При этом следует иметь в виду, что здесь F нормировано не относительно частоты среза, соответствующей уменьшению коэф­фициента передачи фильтра на 3 дБ, а от­носительно обратной величины группового времени задержки при = 0. Такой спо­соб нормировки, однако, малопригоден.

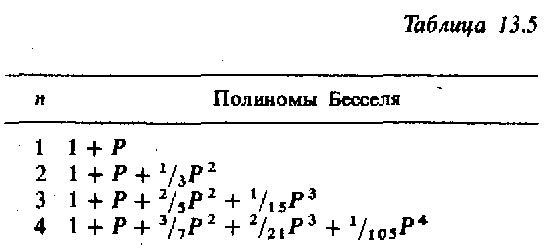
Поэтому был произведен пересчет коэффи­циентов с; и выполнено разложение поли­нома знаменателя на сомножители второ­го порядка. Полученные в результате коэффициенты аi и bi, соответствующие знаменателю передаточной функции (13.4) для фильтров до десятого порядка, приве­дены в табл. 13.6.

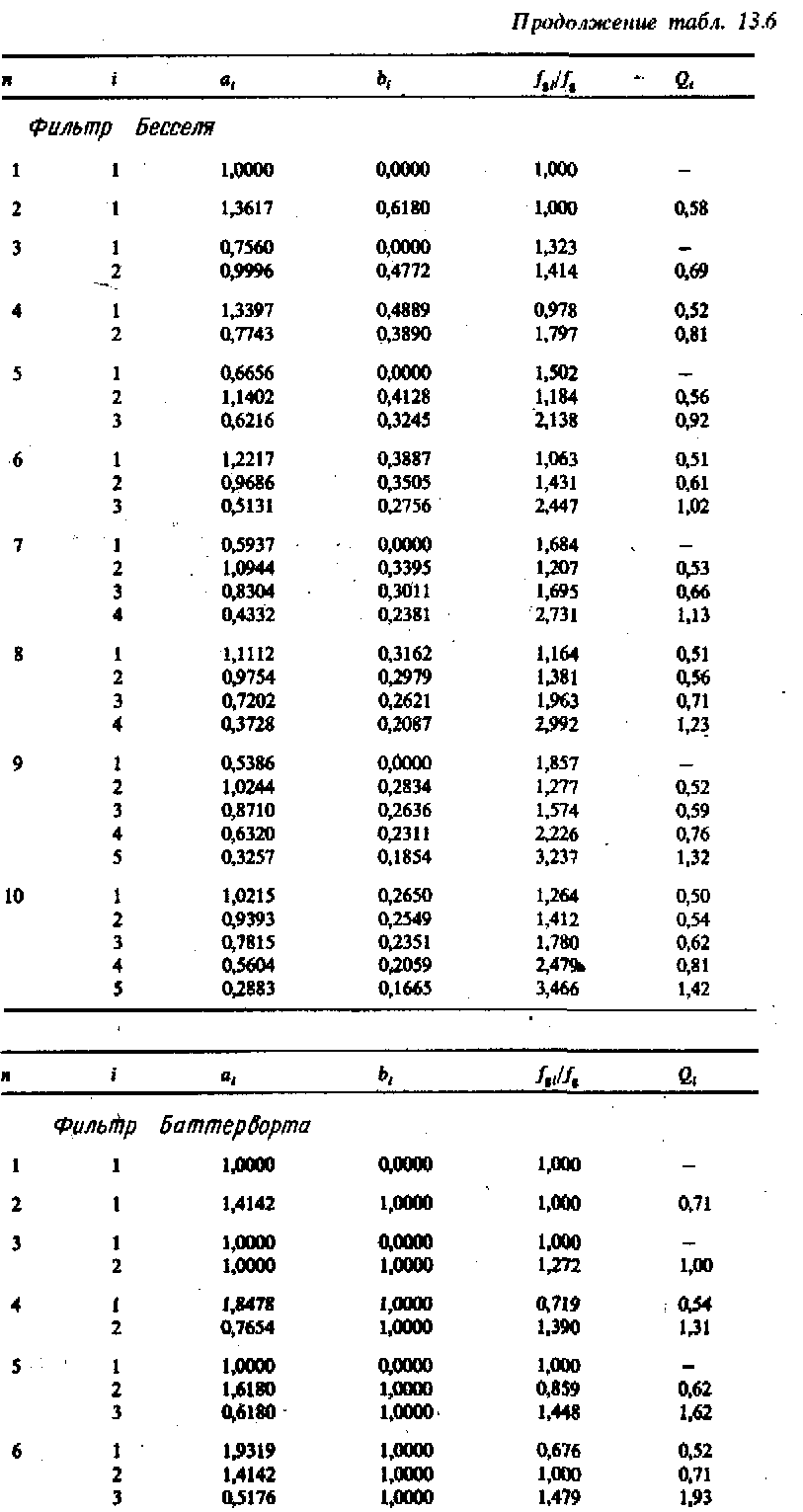
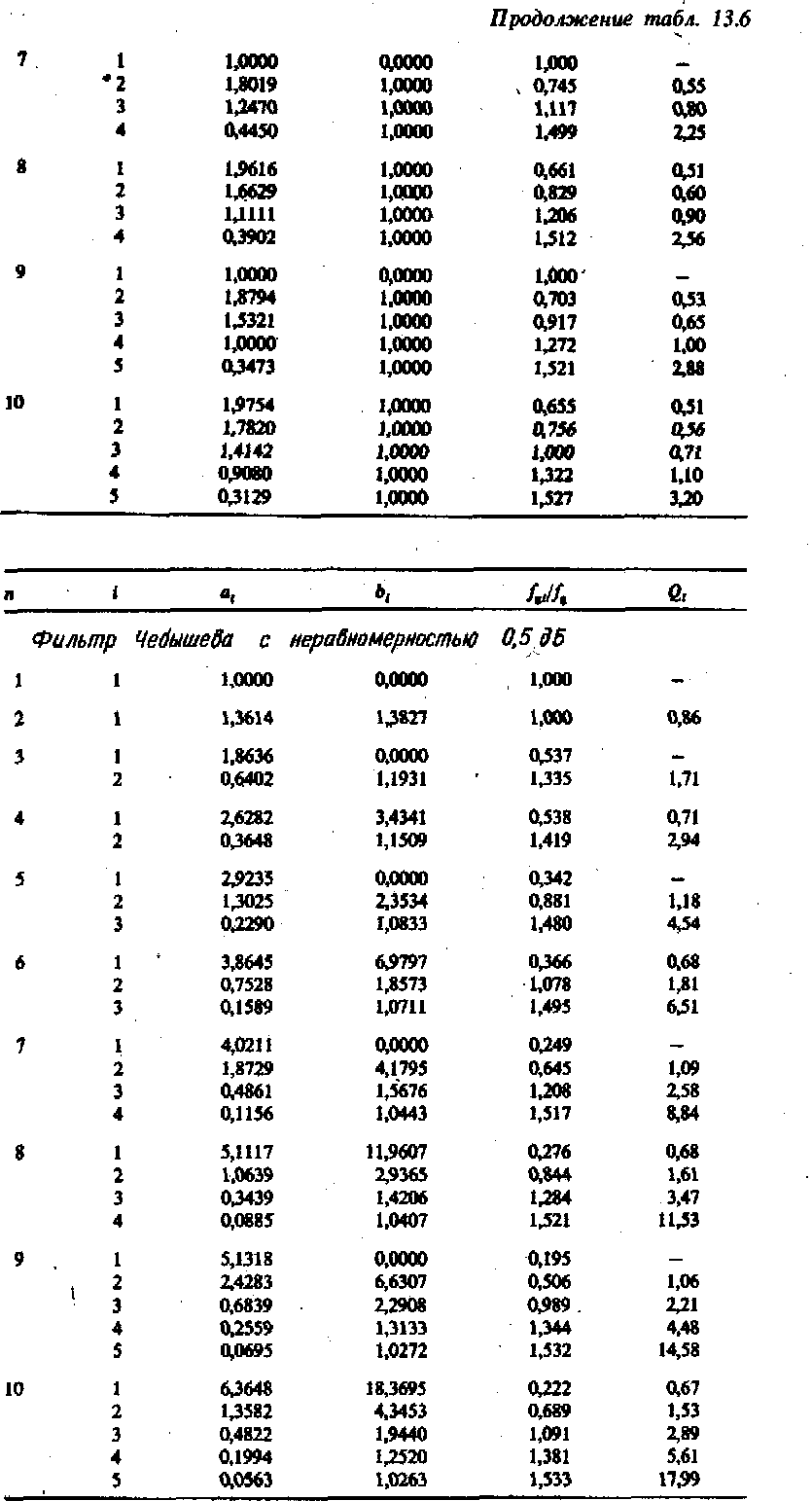
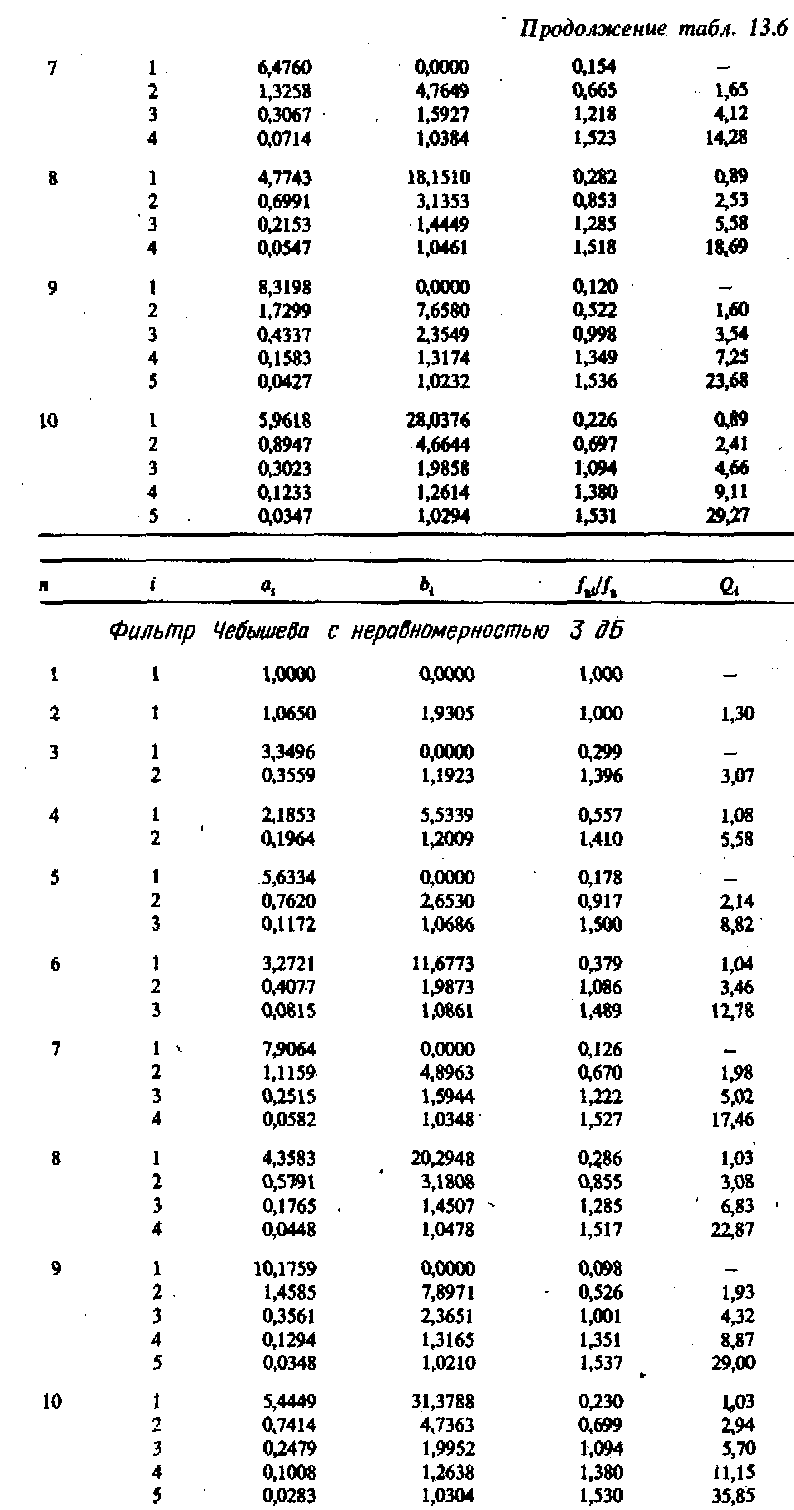
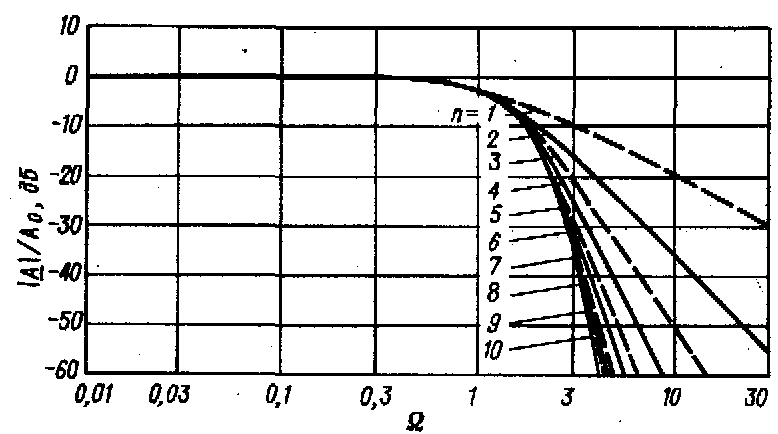
Рис. 13.7. Амплитудно-частотные характеристики ко­эффициента передачи филь­тров Бесселя.

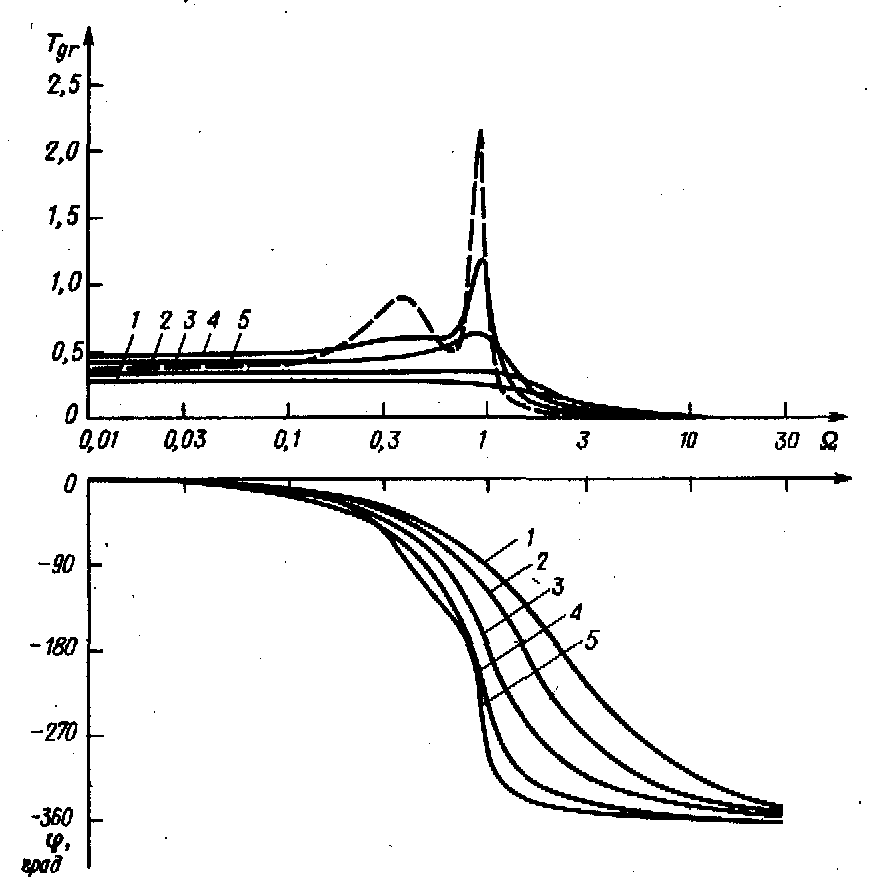
Рис. 13.8. Амплитудно-частотные характеристики группового времени задержки и фазового сдвига

фильтров нижних частот четвертого порядка.

1 -фильтр с критическим затуханием; 2 -фильтр Бесселя;

3-фильтр Баттерворта;

4- фильтр Чебышева с неравномерностью 0,5 дБ;

5-фильтр Чебышева с неравномерностью 3 дБ.

Амплитудно-частотные характеристики коэффициента передачи фильтров Бесселя изображены на рис. 13.7.

Для иллюстрации фазовых искажений рассмотренных фильтров по сравнению с фильтром Бесселя на рис. 13.8 приведены фазово-частотные характеристики и графи­ки зависимости от частоты группового времени задержки для различных филь­тров четвертого порядка. Для их построе­ния наиболее удобно воспользоваться передаточной функцией (13.4), разложенной на множители, и просуммировать фазовые сдвиги и групповое время задержки от­дельных звеньев, второго порядка. При этом с учетом соотношений (13.8) и (13,9в) получим

13.1.4. ОБОБЩЕННОЕ ОПИСАНИЕ ФИЛЬТРОВ

Как было показано, передаточная функ­ция любого фильтра нижних частот может быть представлена в следующей форме:

Порядок фильтра n определяется макси­мальной степенью Р в выражении (13.11) после того, как выполнено перемножение блоков второго порядка в знаменателе. Он задает асимптотический наклон амплитудно-частотной характеристики коэффициен­та передачи, равный — n • 20 дБ на декаду-Вид частотной характеристики определяет­ся как порядком, так и типом фильтра. На­ибольшее применение находят фильтры Баттерворта, Чебышева и Бесселя, которые отличаются лишь значениями коэффициен­тов ai и bi передаточной функции (13.11). Значения соответствующих им коэффи­циентов для фильтров до десятого порядка приведены в табл. 13.6. В таблице приве­дены также значения нормированных ча­стот среза fgi/fg для каждого сомножителя (звена фильтра) выражения (13.11). Эти зна­чения не учитываются при расчетах одна­ко они могут использоваться для проверки работы каждого звена фильтра.

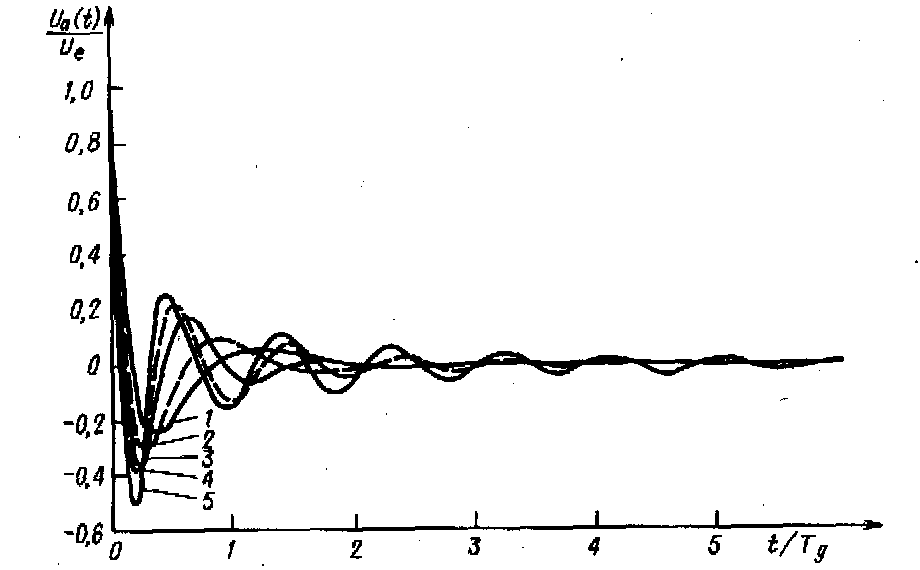
Рис. 13.9. Переходные характеристики фильтров верхних частот четвертого порядка при ступенча­том входном сигнале.

Кроме того, в таблице даны значения добротности полюсов Qi звеньев фильтров. Она определяется по аналогии с доброт­ностью избирательных фильтров, опреде­ленной в разд. 13.6.1:

Чем больше добротность, тем больше склонность фильтра к генерации. Доброт­ность фильтра с действительными полюса­ми не превышает 0,5.