Применение степенных рядов

Другой способ аппроксимации функции sin х состоит а ее представлении в виде степенного ряда:

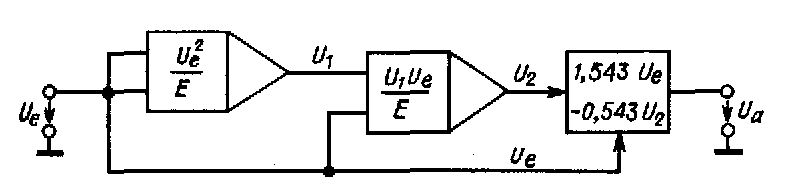
Рис. 11.28. Аппроксимация минусной функции рядом.

Для уменьшения затрат обычно исполь­зуют только два первых члена ряда, что приводит к появлению погрешности вос­произведения функции. Ограничив изме­нение аргумента можно минимизировать эту по­грешность, несколько изменив значения коэффициентов разложения [11.3]:

В этом случае погрешность для значений х = 0, + 0,96, ± /2 равна нулю, а между этими точками абсолютная ошибка не пре­вышает 0,57% амплитуды. Коэффициент нелинейных искажений составляет 0,6%. Он может быть уменьшен с помощью незна­чительного изменения коэффициентов до 0,25%, что оказывается несколько лучше, чем при кусочной аппроксимации для 2 х 3 точек излома, рассмотренной выше. Влияние погрешностей в точках излома кривой оказывается весьма существенным, если выходной сигнал будет подвергаться дифференцированию.

Для схемотехнической реализации по­ложим

Далее будем считать, что U_a = U_e; тогда из формулы (11.35) следует, что

Блок-схема реализации этого уравнения приведена на рис. 11.28. При этом в каче­стве амплитуды входного сигнала U_e была выбрана константа Е блока умножения. С блоками умножения мы познакомимся в следующем разделе.

Дифференциальный усилитель

Еще один способ синусной аппроксима­ции основан на том, что функция гиперболического тангенса (th х) для малых значе­ний х близка к функции sinx Эта функция может быть достаточно просто реализова­на с помощью дифференциального усили­теля, изображенного на рис. 11.29. Как бы­ло показано в разд. 11.7.1, для дифферен­циального усилителя из формулы (11.29) следует, что

Используя эти соотношения, получим

Операционный усилитель формирует раз­ность коллекторных токов в соответствии с соотношением

Отсюда следует, что

Рис. 11.29. Аппроксимация синусной функции с помощью дифференциального усилителя.

Эту функцию приближенно при можно интерпретировать как синус:

Качество аппроксимации синусной харак­теристики зависит от выбора значения Uе. Хорошая аппроксимация может быть по­лучена, если выбрать U_e = 2,8 U_T72 мВ. При этом погрешность воспроизведения функции минимальна, а амплитуда выход­ного сигнала равна 0,86I_ER₂. Абсолютная ошибка составляет при этом не более 3% амплитудного значения, причем макси­мальное значение ошибка принимает на краях заданного диапазона. Обрезав вер­шины аппроксимирующей функции с по­мощью двух диодов, можно уменьшить коэффициент искажений с 1,3% примерно до 0,4%.

Функция cos х

Функция cos x при изменении аргумента в диапазоне 0х может быть реализована с помощью уже описанной схемы, используемой для формирования функции sinx. Для этого требуется, чтобы значения входного сигнала находились в диапазоне от 0 до Ueмакс и было сформировано вспомогательное напряжение

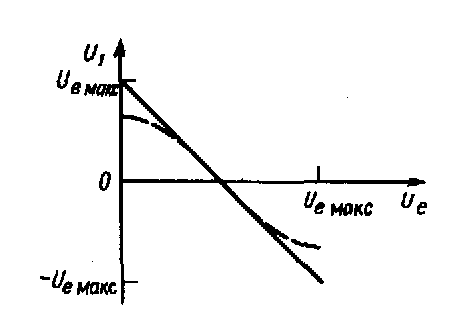
Рис. 11.30. График вспомогательного напряже­ния для реализации косинусной функции, изоб­раженной пунктиром.

Из рис. 11-30 видно, что при этом сразу по­лучается первое приближение для функции cosx, Скругление прямой в областях мак­симума и минимума выполняется с по­мощью блока формирования функции sinx (рис. 11-31). Как видно из рисунка, для это­го дополнительно нужно использовать од­ну простую схему суммирования.

Одновременное формирование функции sin x и cos х для аргумента, изменяющегося в диапазоне —x

Описанные до сих пор устройства поз­воляют формировать функции sin x и cos x для одного полупериода. Если же измене­ние аргумента превышает период, то для реализации указанных функций исполь­зуют их первое приближение в виде треу­гольной функции, которое затем сглажи­вается с помощью вышеупомянутых устройств. Вид треугольных напряжений показан на рис. 11.32.

Напряжение U₁ служит для аппрокси­мации функции cos x. Для входного напря­жения Ue, большего нуля, оно идентично напряжению U₁ на рис. 11.30. При Ue < 0 оно представляет собой зеркальное ото­бражение относительно оси у. Для его опи­сания можно использовать выражение (11.38), заменив Ue на Ue:

Более сложно описывается функция sinx. Для ее представления следует рассмотреть три области изменения входного напряже­ния:

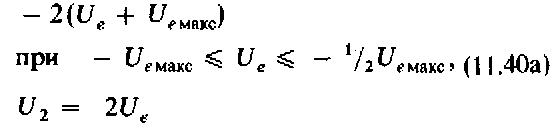
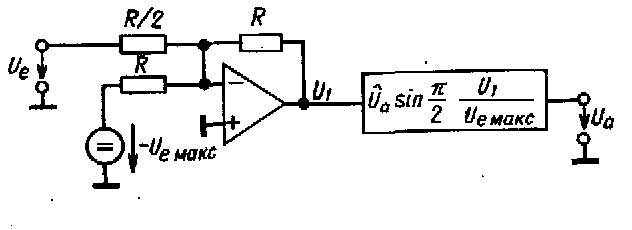
Рис. 11.31. Реализация косинусной функции с помощью схемы синусной функции.

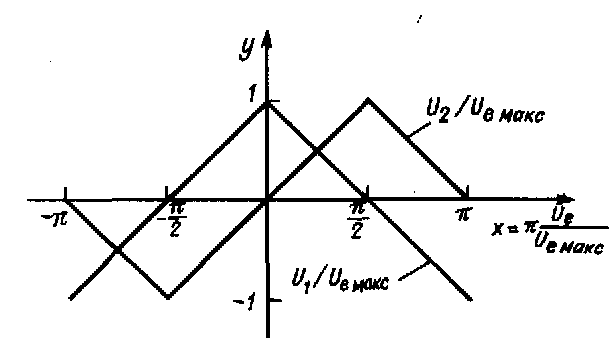
Рис. 11.32. Графики вспомогательных на­пряжений для реализации синусной и ко­синусной функций в диапазоне —x.

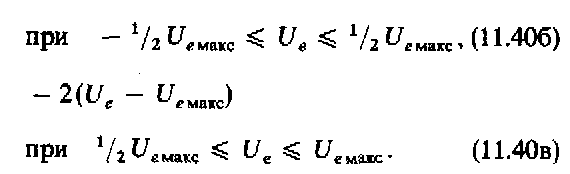
При реализации таких функций лучше все­го использовать точные функциональные преобразователи, описанные ниже.

11.7.5. ПЕРЕСТРАИВАЕМЫЕ ФУНКЦИОНАЛЬНЫЕ СХЕМЫ

На рис. 11.26 была показана диодная схема для кусочной аппроксимации функ­ций многоугольниками. Расчет таких схем может быть выполнен только приближен­но, так как нужно принимать во внимание прямое напряжение диодов и их взаимное влияние. Кроме того, наклоны аппрокси­мирующих участков уже заданы структу­рой схемы. Поэтому такие схемы могут ис­пользоваться для оптимальной аппрокси­мации конкретных функций и не поддают­ся простой перестройке.

На рис. 11.33 приведена схема, которая позволяет с помощью отдельных потен­циометров устанавливать точки излома ап­проксимирующей кривой и наклон от­дельных ее участков. Ветвь схемы, в которой используются операционные усилители ОУ 1 и ОУ 2, предназначена для задания параметров одного участка при положительном значении входного на­пряжения, а ветвь, в которую входят уси­лители ОУ 5 и ОУ б, - для отрицательного напряжения. Усилитель ОУ 4 задает на­клон аппроксимирующей кривой в нуле.

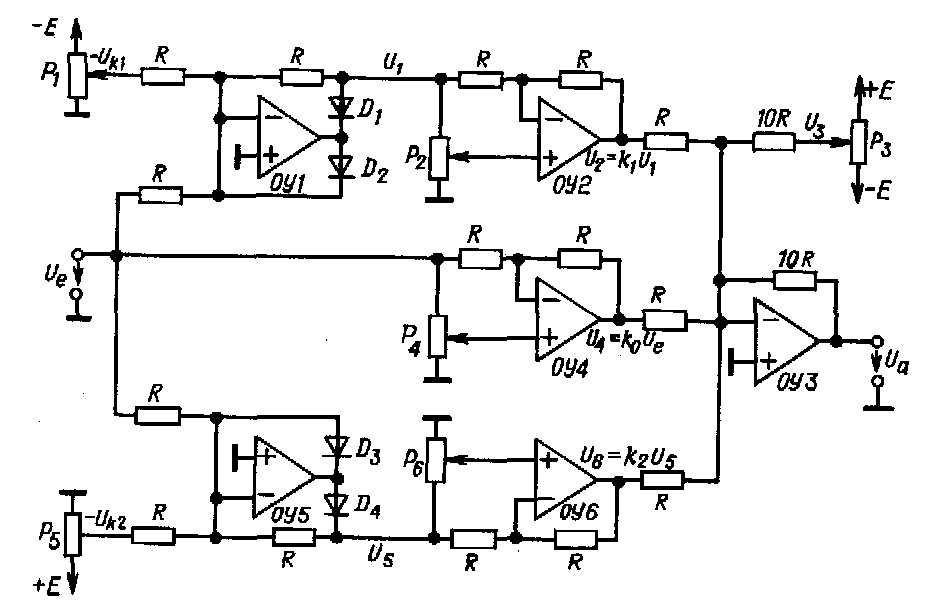
Рис. 11.33. Настраиваемая функциональная схема.

Необходимое для аппроксимации число участков задается путем дополнительного включения в схему нужного числа ветвей.

Усилители ОУ 2, ОУ 4 и ОУ 6 предста­вляют собой биполярные передаточные звенья с n = 1 (см. схему на рис. 11.5). Коэффициент их усиления может быть установлен в диапазоне — 1k1 с помощью соответствующего потенцио­метра. Выходные напряжения суммируют­ся с помощью операционного усилителя ОУ 3. К ним нужно добавить постоянное напряжение, величина которого регули­руется потенциометром Р₃.

При малых значениях входного напря­жения работает только усилитель ОУ 4. Его вклад в выходное напряжение равен

Напряжения U₁ и U₅ в этом случае равны нулю, так как диоды D₁ и D₄ закрыты, а усилители ОУ 1 и ОУ 5 замкнуты откры­тыми диодами D₂ и D_3.

Когда входное напряжение превысит уровень U_k1 диод D₁открывается и напря­жение на выходе усилителя ОУ 1 будет равно

Усилитель ОУ 1 работает в режиме однополупериодного выпрямителя с .положи­тельным смещением U_k1. Аналогично ве­дет себя усилитель ОУ 5 для отрицатель­ного входного напряжения:

Для задания наклона выходного напряже­ния Ua схемы можно записать следующее соотношение:

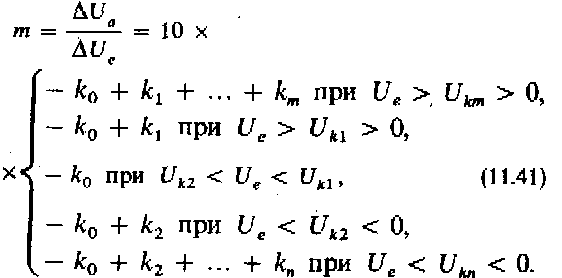
В качестве примера рассмотрим форму напряжений для реализации функции U₂ из рис. 11.32. Наклон нулевого сегмента, согласно формуле (11.40б), должен быть равен +2. Отсюда получаем Значение k₀ = 0,2. Для положи­тельных входных напряжений за точкой перегиба необходимо обеспечить наклон с m= —2. Из формулы (11-41) для этого участка получим

откуда k₁ = 0,4. Аналогично получим k₂=-0,4. Результирующие графики напря­жений приведены на рис. 11.34.

Настройка схемы для аппроксимации заданной функции выполняется достаточно просто даже тогда, когда в распоряжении имеются только некалиброванные потенциометры Для этого сначала устанавли­вают максимальные значения всех напря­жений, соответствующих точкам излома и наклонам участков. После этого задают входное напряжение Ue равное нулю. В этом. случае Ue < Uki, и можно уста­навливать начальное значение напряжения

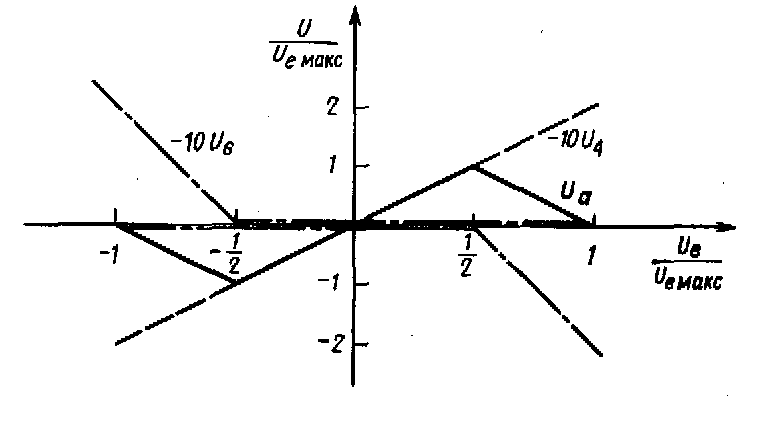
Рис. 11.34. Графики линейно изменяющихся напряжений для получения напряжения U₂ (рис. 11.32).

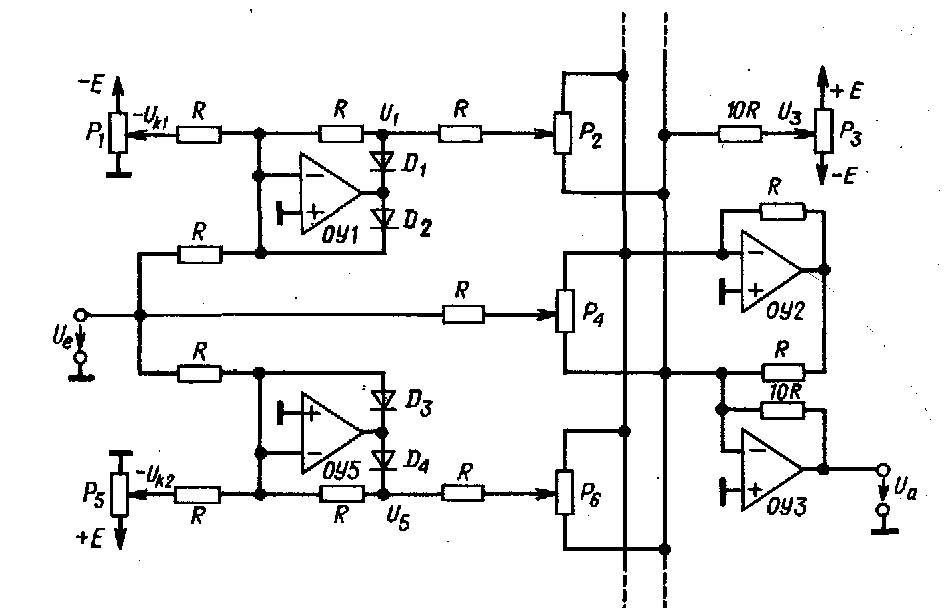
Рис. 11.35. Упрощенная настраиваемая функциональная схема.

аппроксимирующей кривой в нуле (Ua(0)) с помощью потенциометра Pз. После это­го задают входное напряжение Ue = Uk₁ и с помощью потенциометра Р₄ устана­вливают необходимую величину выходно­го напряжения Ua(Uk₁), Таким образом за­дают коэффициент k₀, затем настраивают Р₁ до тех пор, пока не начнет изменяться выходное напряжение. Теперь потенцио­метр P₁ настроен на точку излома Uk₁. За­тем устанавливают входное напряжение Ue соответствующее следующей точке перегиба (в данном примере конечная точ­ка), и подстройкой Р₂ добиваются необхо­димого значения выходного напряжения Ua Таким образом задают коэффициент k₁. Аналогичные действия выполняют для всех остальных точек перегиба.

В случае когда для настройки используются некалиброванные потенциометры, можно провести упрощение схемы. Бипо­лярные передаточные звенья можно заме­нить обычными потенциометрами, как по­казано на рис. 11.35, где они включены на входе схемы вычитания. Эта схема по­строена в соответствии со структурой, по­казанной на рис. 11.2, на операционных усилителях ОУ 2 и ОУ 3.