9 3D Digital Elevation Model Generation |
379 |
9.3 DEM Generation from InSAR
Interferometric Synthetic Aperture Radar (InSAR) is the combination of SAR and interferometry techniques. SAR systems, operating at microwave frequencies, provide unique images representing the geometrical and electrical properties of the surface in nearly all weather conditions. DEM generation from InSAR is an active sensing process which is largely independent of weather conditions and can operate at any time throughout the day or night. A conventional SAR only produces 2D images reflecting the location of a target in the along-track axis, which is the axis along the flight track (azimuth range, X), and the across-track axis, which is the axis defined as the range from the SAR to the target (slant range, Y ). The altitudedependent distortion of SAR images can only be viewed in X and Y with ambiguous interpretation. Therefore, it is impossible to use a single SAR image to recover surface elevation. The development of InSAR techniques has enabled measurement of the third dimension (the elevation), which relies on the phase difference from two SAR images covering the same area and acquired from slightly different angles.
DEM generation from satellite-based SAR was reviewed by Toutin and Gray [151] with four different categories: stereoscopy, clinometry, polarimetry and interferometry (InSAR). Stereoscopy employs the same geometric triangulation principle used in optical stereoscopy for recovering elevation information, clinometry utilises the concept of shape from shading and polarimetry works on a complex scattering matrix based on a theoretical scattering model for tilted and slightly rough dielectric surfaces to calculate the azimuthal slopes, hence generating the elevation. InSAR also employs triangulation, but in a different implementation to stereoscopy, and can measure to an accuracy of millimeters to centimeters, which is a fraction of the SAR wavelength, whereas the other three methods are only accurate to the order of the SAR image resolution (several meters or more) [129]. DEM generation from InSAR is introduced in this section. For the other categories, please refer to [151] for details.
9.3.1 Techniques for DEM Generation from InSAR
The concept of incorporating interferometry to radar for topographic measurement can be traced back to Roger and Ingalls’ Venus research in 1969 [127]. Zisk used the same method for moon topography measurements [184], while Graham employed InSAR for Earth observation by an airborne SAR system [56]. However the real development of InSAR in DEM generation from spaceborne SAR instruments has been supported by the availability of suitable globally acquired SAR data from ERS-1 (1991), JERS-1 (1992), ERS-2 (1995), RADARSAT-1 (1995), SRTM (2000), Envisat (2002), RADARSAT-2 (2007), and TanDEM-X (2010). The technique has been considered mature since the late 1990s. The following section introduces InSAR concepts and their application to DEM generation.
380 |
H. Wei and M. Bartels |
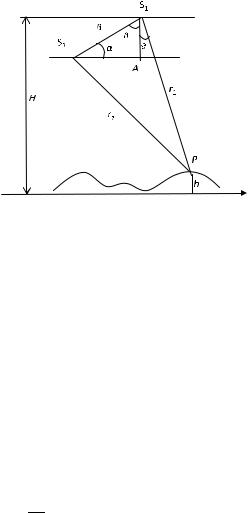
Fig. 9.5 InSAR imaging geometry: The radar signal is transmitted from antenna S1 and received simultaneously at S1 and S2. The phase difference of the two echoes is proportional to r , which depends on the baseline angle α, look angle θ , satellite altitude H , range vectors r1 and r2, and target elevation h
9.3.1.1 Basic Principle of InSAR in Elevation Measurement
InSAR in DEM generation requires that two SAR images of a target are acquired from different positions by a sensor (or sensors) with nearly the same observation angles. The phase difference between these two observations is then used to derive the elevation. The two SAR images can be taken at the same time (single-pass interferometry) or at different times (repeat-pass interferometry) over the target. Figure 9.5 depicts a simplified InSAR imaging geometry [1]. S1 and S2 are two sensor positions, r1 and r2 are range vectors from the two sensors to the target point P with elevation h, satellite altitude is H , the baseline is B, α is the baseline orientation
angle, and θ is the look angle. |
|
A complex signal returning to the SAR from the target P is expressed by |
|
S = Aej φ |
(9.7) |
where A is the amplitude and φ is the phase. Two complex SAR images (a ‘master’ and a ‘slave’) are formed from positions S1 and S2. Therefore the phase difference ψ between S1 and S2 is directly related to the path difference between r1 and r2, as follows:
ψ = − |
4π |
(9.8) |
λ r |
where λ is the SAR signal wavelength, and r = r2 − r1.
The imaging geometry in Fig. 9.5 demonstrates the relationship of B, r1, r2, α, and θ . In order to derive the formula which expresses the relationship quantitatively, two additional elements are introduced: one is point A, a perpendicular intersection point of line S1A and line S2A, and the other is angle β, the complementary angle of 90◦ to α in the right angled triangle S1S2A. According to a trigonometric theorem,
applied to the triangle S1S2P , the following equation is satisfied: |
|
|
|
||||||||||
|
r22 |
− r12 − B2 |
|
2 |
r2 |
|
B2 |
|
2r |
B cos(β |
|
θ ) |
(9.9) |
cos(β + θ ) = |
|
−2r1B |
or |
r2 = |
+ |
− |
+ |
||||||
|
1 |
|
1 |
|
|
|
|||||||
In Eq. (9.9), cos(β + θ ) can be expanded to |
|
|
|
|
|
|
|
|
|
||||
|
cos(β + θ ) = cos β cos θ − sin β sin θ |
|
|
|
(9.10) |
||||||||
9 3D Digital Elevation Model Generation |
381 |
In the right angled triangle S1S2A of Fig. 9.5, sin β = cos α and cos β = sin α. Substituting these into the right-hand side of Eq. (9.10), we have
cos(β + θ ) = sin α cos θ − cos α sin θ = − sin(θ − α) |
(9.11) |
Substituting Eq. (9.11) to Eq. (9.9), the relationship of B, r1, r2, α, and θ is expressed in Eq. (9.12), and the target elevation h can be calculated from Eq. (9.13) based on the geometric relation shown in Fig. 9.5.
|
− |
|
= |
r22 |
2r1B |
2 |
|
sin(θ |
|
α) |
|
− r12 − B |
(9.12) |
||
|
= H − r1 cos θ |
|
|||||
|
|
h |
|
(9.13) |
|||
In Eq. (9.12), r1 is replaced by r , and r2 by r + r , then it can be re-written as
sin(θ |
− |
α) |
= |
(r + r)2 − r2 − B2 |
(9.14) |
|
2rB |
||||||
|
|
|
Replacing cos θ in Eq. (9.13) by sin(θ − α) in such a way that it can be rewritten as
|
cos α 1 − |
|
sin2 |
|
− sin α sin(θ − α) |
|
h = H − r |
|
(θ − α) |
(9.15) |
In practice, the SAR altitude H , the baseline B, and the baseline orientation angle α are estimated from knowledge of the orbit, and the range r , half the roundtrip distance of radar signal, is measured by the SAR internal clock. Knowing the phase difference ψ from the interferometric fringes of two SAR images, the path difference r can be calculated from Eq. (9.8), hence sin(θ − α) can be derived from Eq. (9.14), and finally the elevation value is calculated from Eq. (9.15).
The phase difference between the two SAR images is normally represented as an interferogram, an image which is the product of the complex master image convolved with the complex slave image. It is important to appreciate that only the principal values of the phase, (i.e. modulo 2π ), can be measured from the interferogram. The 2π phase difference corresponds to one cycle of interferometric fringe. The total path difference of the two receivers is multiples of the radar wavelength, (i.e. multiples of 2π in terms of phase). The process of phase unwrapping estimates this integer number in the interferometry. It is a key process in DEM generation from InSAR.
In many cases, the InSAR imaging geometry may differ from that demonstrated in Fig. 9.5. However, the principle of deriving the target elevation from the interferogram is similar and involves the following two steps:
1.Find out the path difference from the phase difference.
2.Calculate the topography based on the path difference with other known geometric parameters.
Figure 9.5 is a simplified model and the phase of SAR signals contains other information beyond topography. For a detailed description of InSAR and a better understanding of the signal modeling, please refer to [72].