5. Двоичная и десятичная системы счисления. Перевод из одной системы в другую. Задание фал с помощью десятичных чисел.

Задание ФАЛ с помощью 10-тичных чисел( правила перевода из 10 в 2):

• Перевод из 10 в 2 осуществляется с помощью деления на 2

• Число делится на 2, остаток от деления является младшим разрядом двоичного числа. Частное от деления вновь делится на 2. Остаток является следующим разрядом.

• Деление заканчивается. Когда частное от деления будет <2. Это частное является старшим разрядом двоичного числа.(записывается снизу вверх)

ФАЛ задается с помощью десятичных эквивалентов тех двоичных наборов, на которых f=1. Достоинства этого метода : компактность.( ТИ от 4х переменных, f=0,4,5,7,9,10,12,13,15)

Для перевода двоичного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 2, и вычислить по правилам десятичной арифметики.

6. Аксиомы алгебры логики. Законы нулевого и единичного множества, повторения, двойного отрицания, логического нуля, логической единицы.

Аксиомы:

• =1,

• 0*0=0, 0*1=1*0=0,1*1=1

• 0v0=0, 0v1=1v0=1, 1v1=1

Законы:

• Закон нулевого множества: 0*x=0, 0vX=X

• Закон единичного множества: 1*x=x, 1vX=1

• Закон повторения: x*x=x, XvX=X

• Закон двойного отрицания: =x

• Закон логического нуля: x* =0

• Закон логической единицы: Xv =1

7. С уперпозиция фал. Переместительный, сочетательный и распределительный законы. Закон упрощения. Формулы де Моргана.

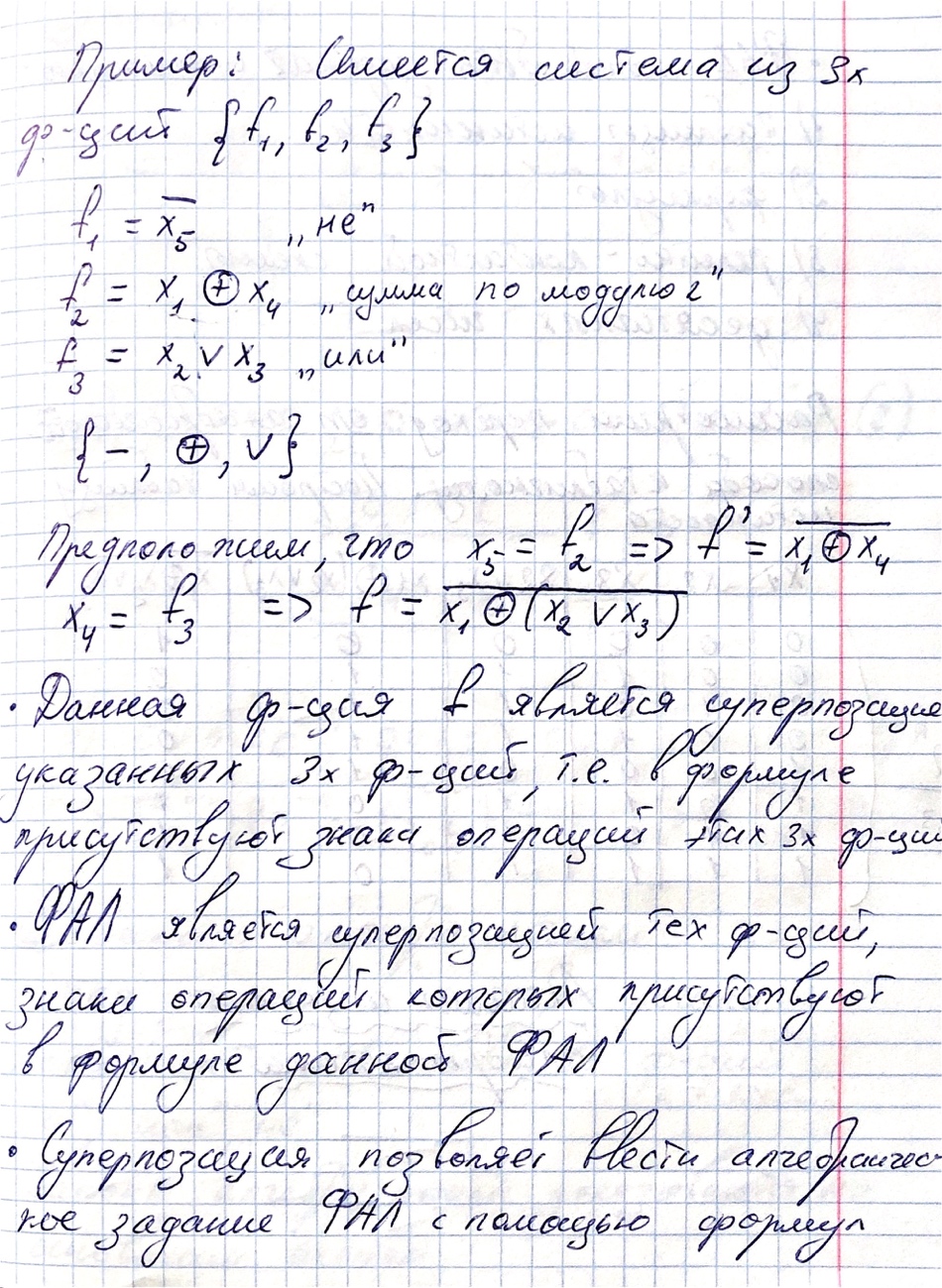
Законы:

• Переместительный: x1*x2=x2*x1

• Сочетательный: x1(x2*x3)=x3(x1*x2), X1v(X2vX3)=(X1vX2)vX3

• Распределительный: X1*(X2vX3)=X1*X2vX1*X3, X1vX2*X3=(X1vX2)(X1vX3)

• Закон упрощения: X1*X2vX1* =X1, (X1vX2)*(X1v )=X1

Формулы де Моргана:

• = v отрицание конъюнкции равно дизъюнкции отрицаний.

• = * отрицание дизъюнкций равно конъюнкции отрицаний.

8. Стандартные формы фал.

Рассмотрим задачу как по таблице истинности получить алгебраическую запись ФАЛ. Пусть надо построить схему управления электродвигателя. Схема должны иметь 3 входа (х1,х2,х3 - кнопки) и должна работать по след.алгоритму: двигатель включен если нажато нечетное число кнопок и выключенное - если честное. Построим таблицу истинности: каждая из последовательных цепей соответствует разрешенным наборам и обеспечивает путь проводимости в схеме при данном входном наборе.

Х1	Х2	Х3	f	Входные наборы, на которых f=1 будем называть разрешенными наборами, определяют условия включения двигателя. Входные наборы, на которых f=0 будем называть запрещенными, определяют условия не включения. F= * *X3 v *X2* v X1* * v X1*X2*X3
0	0	0	0	з
0	0	1	1	Р
0	1	0	1	Р
0	1	1	0	З
1	0	0	1	Р
1	0	1	0	З
1	1	0	0	З
1	1	1	1	Р

Полученное выражение называется ДСНФ- дизъюнктивная совершенная(один.числ. перем). Каждая конъюнкция соответствует одному из разрешенных наборов, число букв в конъюнкции равно числу переменных f. Данная форма записи является стандартной, т.е любую ФАЛ с помощью аналогичного процесса можно записать в след.виде: f= …* , где .

Каждая из параллельных цепей сети соответствует запрещенным наборам. Обеспечивает «барьер» проводимости ( ОБРЫВ) при данном наборе. F=(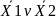 vX3) *( X2v )*( X1v v ) * (X1vX2vX3). КСНФ – конъюнктивная совершенная форма ( конъюнкция дизъюнкций)

f=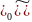 …v )