
- •Часть II
- •8 Дифференциальное исчисление функций нескольких переменных
- •8.1 Функции двух независимых переменных
- •8.2 Частные производные
- •9.3 Полный дифференциал
- •8.4 Касательная плоскость и нормаль к поверхности
- •8.5 Экстремумы функций двух переменных
- •8.6 Условный экстремум
- •8.7 Наибольшее и наименьшее значения функции
- •8.8 Метод наименьших квадратов
- •8.9 Производная по направлению. Градиент
- •Задачи для самостоятельного решения
- •9 Кратные, криволинейные и поверхностные интегралы. Элементы теории поля
- •9.1 Двойной интеграл
- •9.2 Перемена порядка интегрирования
- •9.3 Вычисление площадей и объемов
- •9.4 Криволинейный интеграл по длине дуги
- •9.5 Геометрические и механические приложения криволинейного интеграла по длине дуги
- •9.5 Криволинейный интеграл по координатам
- •9.6 Формула Грина-Остроградского
- •9.7 Независимость криволинейного интеграла 2-го рода от формы дуги кривой
- •9.8 Геометрические и механические приложения криволинейных интегралов 2-го рода
- •Задачи для самостоятельного решения
- •10 Ряды. Гармонический анализ
- •10.1 Числовые ряды
- •10.2 Степенные ряды
- •10.3 Ряды Тейлора и Маклорена
- •10.4 Тригонометрические ряды Фурье
- •Задачи для самостоятельного решения
- •11 Дифференциальные уравнения
- •11.1 Дифференциальные уравнения первого порядка
- •11.2 Основные типы уравнений первого порядка
- •11.3 Понижение порядка уравнения
- •11.4 Линейные уравнения с постоянными коэффициентами
- •12 Операционное исчисление. Уравнения математической физики
- •12.1 Оригиналы и изображения
- •12.2 Теоремы операционного исчисления
- •12.3 Таблица изображений
- •12.4 Свёртка функций
- •12.5 Нахождение оригинала по изображению
- •12.6 Операционный метод решения дифференциальных уравнений с постоянными коэффициентами. Методы решения уравнений математической физики
- •12.7 Решение систем линейных дифференциальных уравнений с постоянными коэффициентами
- •Задачи для самостоятельного решения
- •13 Теория вероятностей
- •13.1 Классическое определение вероятности
- •Основные свойства вероятности
- •13.2 Теоремы умножения и сложения вероятностей
- •13.3 Формула полной вероятности. Формула Байеса
- •13.4 Схема Бернулли
- •13.5 Функция и плотность распределения вероятностей
- •13.6 Свойства функции и плотности распределения вероятностей
- •13.7 Числовые характеристики случайных величин
- •13.8 Свойства математического ожидания и дисперсии
- •13.9 Основные законы распределения вероятностей случайных величин
- •13.10 Связь между случайными величинами
- •Задачи для самостоятельного решения
- •14 Математическая статистика
- •14.1 Эмпирическая функция распределения. Гистограмма
- •14.2 Точечные и интервальные оценки параметров
- •14.3 Статистические гипотезы
- •Задачи для самостоятельного решения
- •Приложение а. Таблица значений функции Лапласа ф0(х)
- •Приложение б. Основные математические обозначения
9.7 Независимость криволинейного интеграла 2-го рода от формы дуги кривой
Пусть в ограниченной
замкнутой односвязной области D
задана векторная функция (векторное
поле)
![]() ,
непрерывно дифференцируемая в D.
,
непрерывно дифференцируемая в D.
Тогда равносильны следующие утверждения.
1. Выражение
![]() представляет собой полный дифференциал
dU
некоторой однозначной функции
U(M) = U(x; y; z),
определённой в области D:
представляет собой полный дифференциал
dU
некоторой однозначной функции
U(M) = U(x; y; z),
определённой в области D:
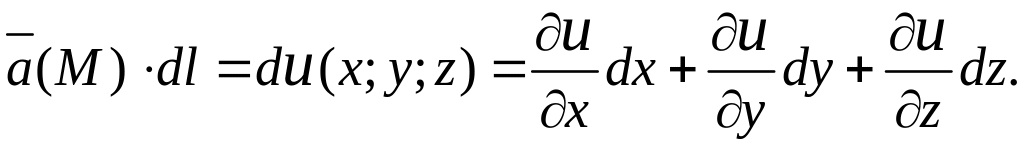
2. В любой точке
M(x,y,z)![]() D
выполняются
соотношения
D
выполняются
соотношения
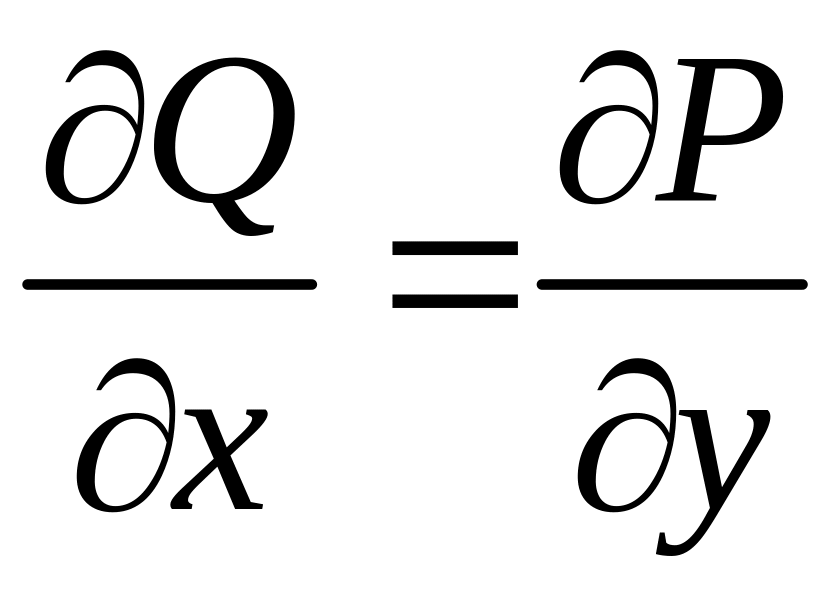 ,
,
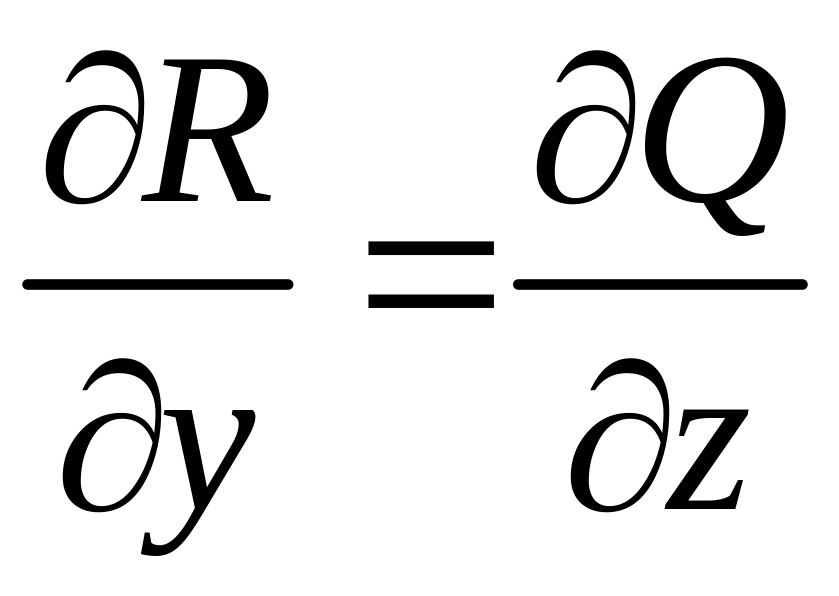 ,
,
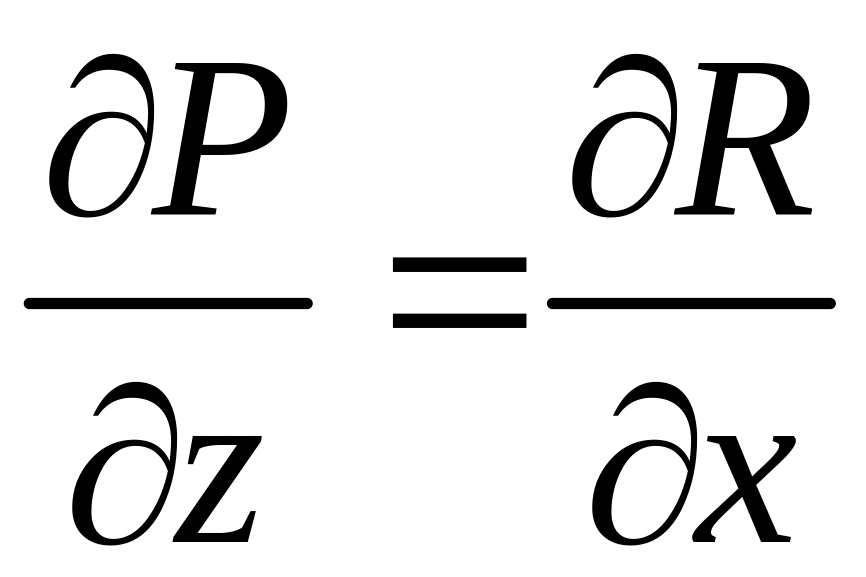 .
.
Если область D
плоская и
![]() ,
то
.
,
то
.
3. Интеграл
![]() ,
взятый по любому замкнутому контуру
L
,
взятый по любому замкнутому контуру
L![]() D
равен нулю:
D
равен нулю:
![]() .
.
4. Интеграл
![]() не зависит от формы дуги ВС
кривой, лежащей в области D.
не зависит от формы дуги ВС
кривой, лежащей в области D.
9.8 Геометрические и механические приложения криволинейных интегралов 2-го рода
1.
Пусть
![]() – сила, совершающая работу А
вдоль пути l,
и функции
– сила, совершающая работу А
вдоль пути l,
и функции
![]() и
и
![]() непрерывны
на кривой l,
тогда
непрерывны
на кривой l,
тогда
![]() .
.
Для
пространственной кривой L
работа A
при перемещении материальной точки M
по дуге BC
из точки B
в точку C
под действием силы
![]() вычисляется по формуле:
вычисляется по формуле:
![]()
2. Площадь правильной области D, ограниченной контуром L, вычисляется по формуле:
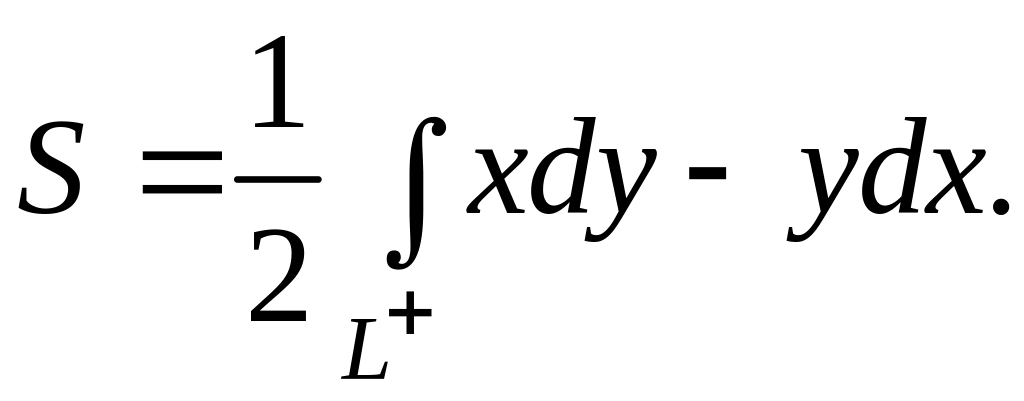
Пример.
Найти работу, производимую силой
![]() ,
вдоль параболы
,
вдоль параболы
![]() от точки А(0; 0)
до точки В(1; 1).
от точки А(0; 0)
до точки В(1; 1).
![]() .
Так как интегрируем по параболе
.
Так как интегрируем по параболе
![]() и При перемещении из точки А
в точку В
и При перемещении из точки А
в точку В
![]() меняется от 0 до 1 (рис.9.3). Так как
интегрируем по параболе
то
меняется от 0 до 1 (рис.9.3). Так как
интегрируем по параболе
то
![]() :
:
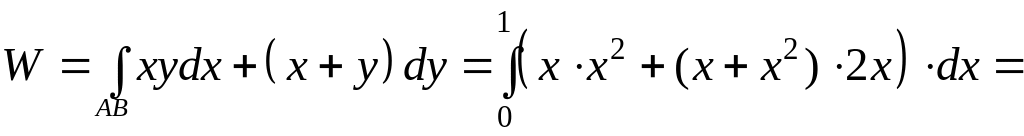
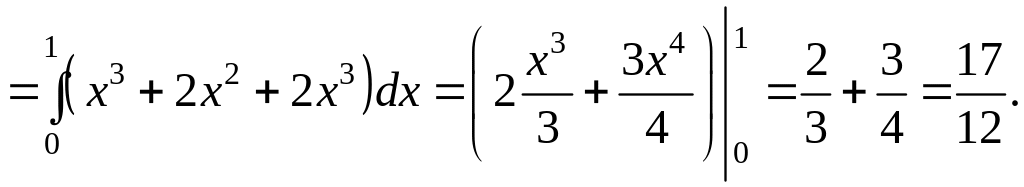
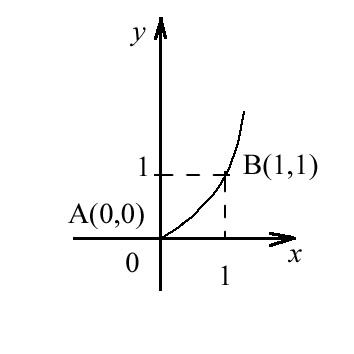
Рис.9.3
Пример. Вычислить криволинейный интеграл 2-го рода
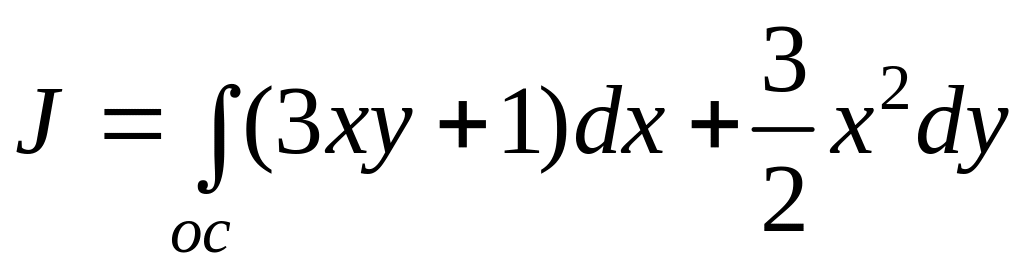
в направлении от точки O(0; 0) к точке C(2; 0) вдоль различных кривых, соединяющих эти точки:
окружности:
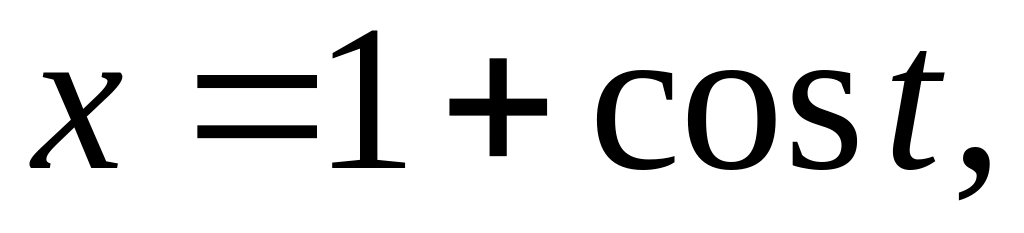
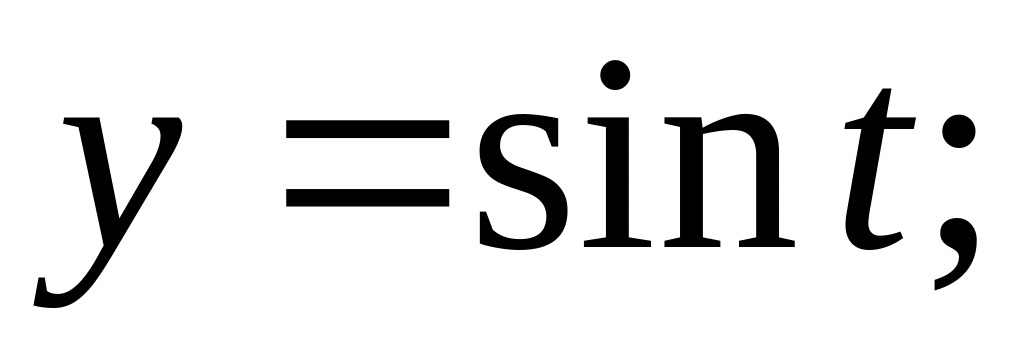
прямой: y = 0;
параболы:
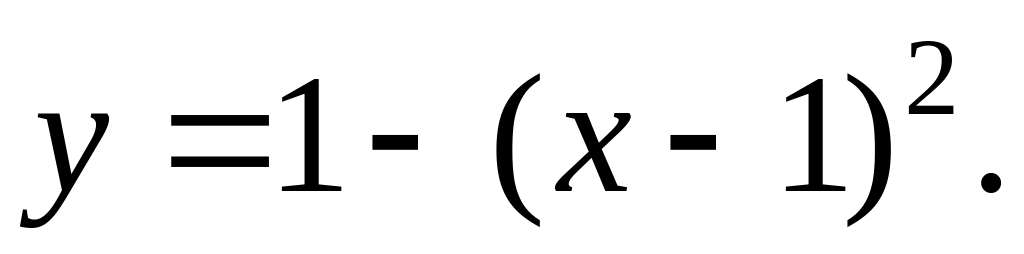
На окружности имеем:
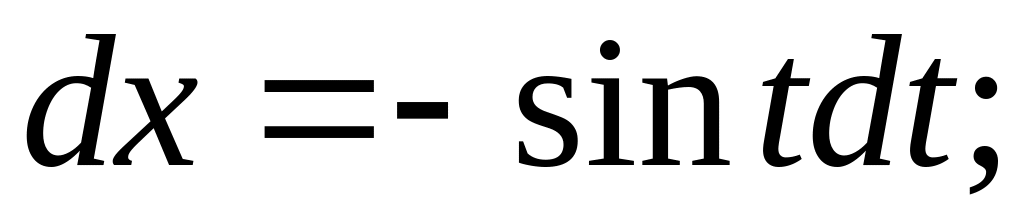
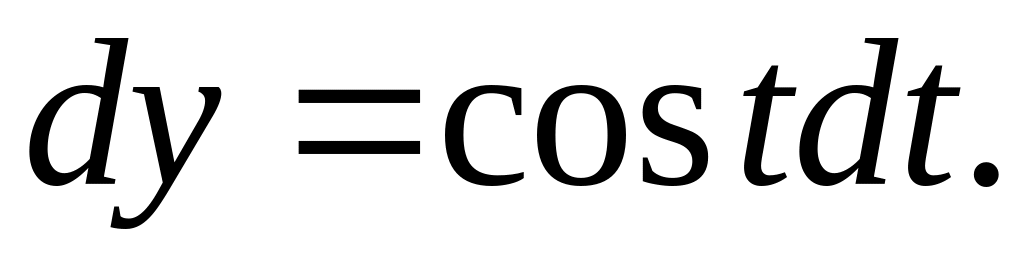
Точке
O(0; 0)
соответствует значение параметра
![]() ,
точке C(2;
0) соответствует значение параметра
,
точке C(2;
0) соответствует значение параметра
![]() .
.
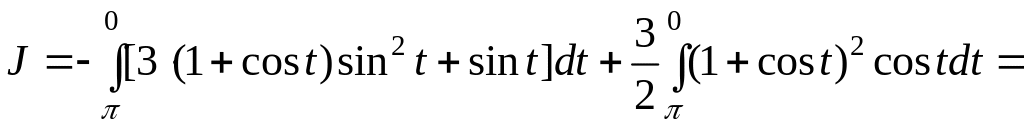
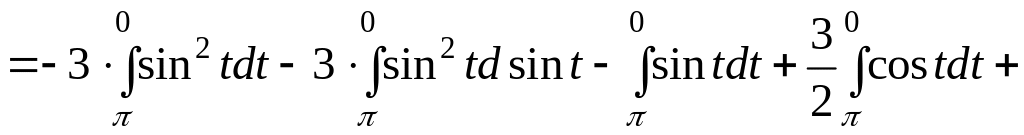
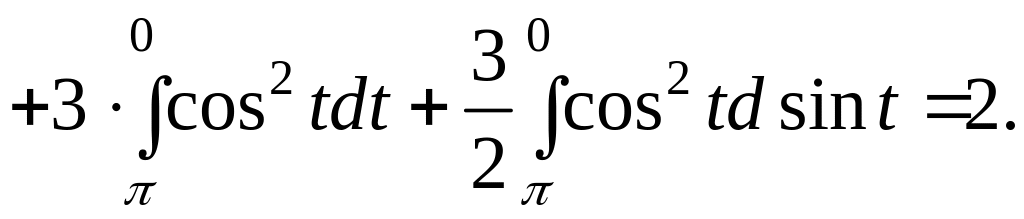
На прямой
 имеем
имеем
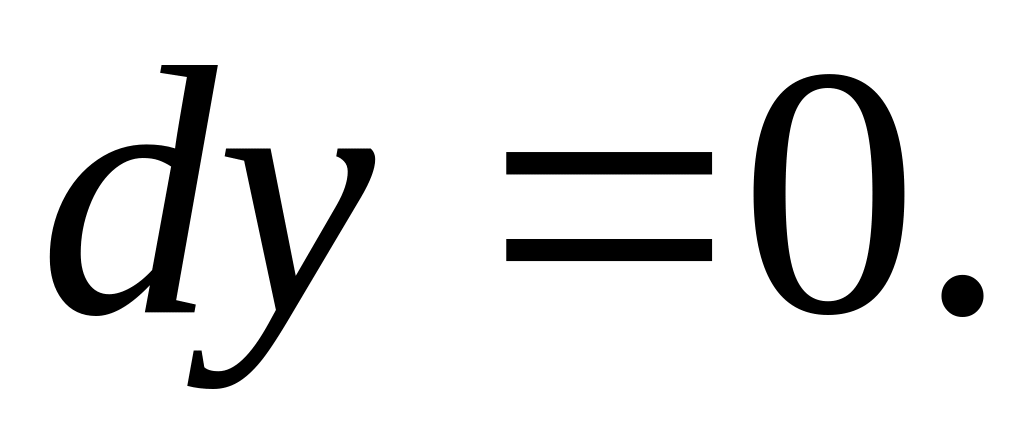
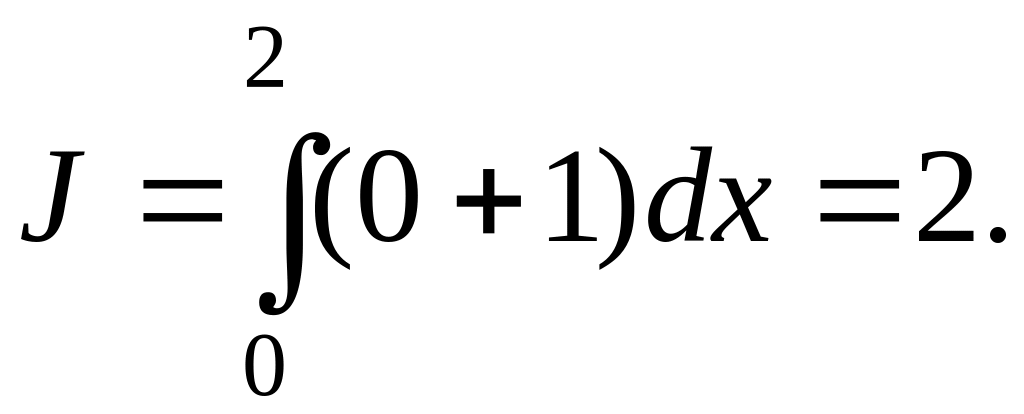
На параболе
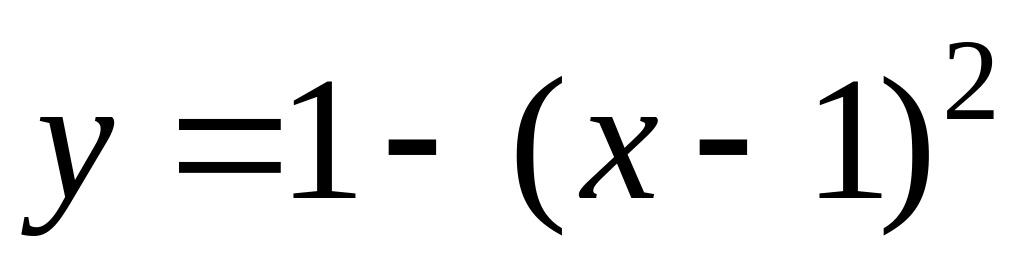 имеем:
имеем:
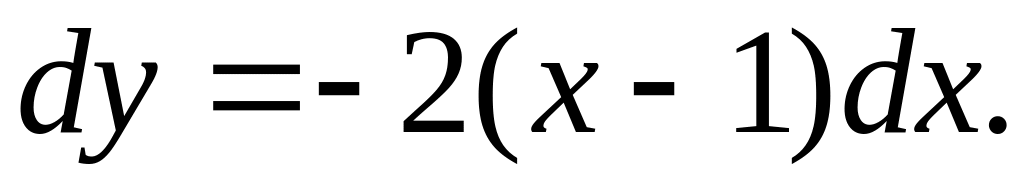
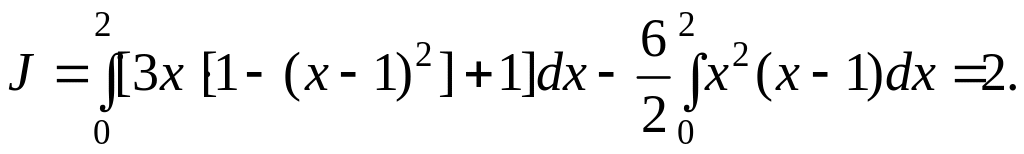
По
условию задачи
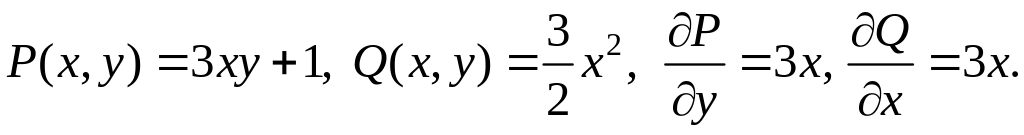
Для любых (x; y)
имеем:
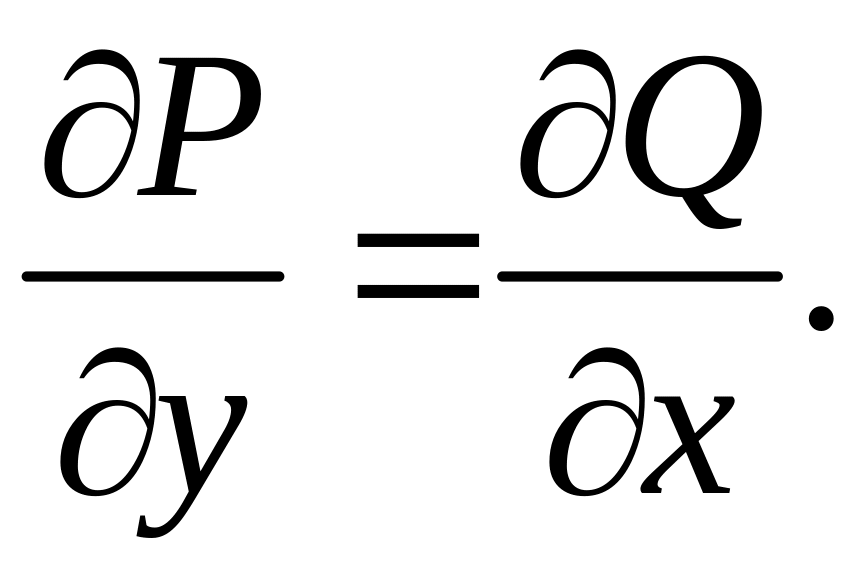 Следовательно, справедливо равносильное
утверждение: интеграл J
не зависит
от формы дуги OC
кривой.
Следовательно, справедливо равносильное
утверждение: интеграл J
не зависит
от формы дуги OC
кривой.
Пример.
Найти работу силового поля
![]()
при перемещении материальной точки по дуге BC окружности
![]()
в направлении,
соответствующем убыванию параметра
t:

На
дуге окружности имеем:
![]()
![]()
![]()
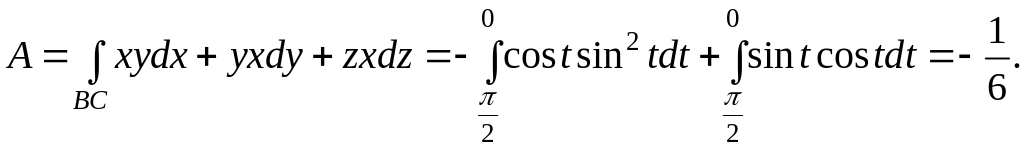
Задачи для самостоятельного решения
№ |
Задание |
|
1 |
Изменить порядок
интегрирования
|
|
2 |
Найти площадь области, ограниченной кривыми
|
|
3 |
Найти объем тела, ограниченного данными поверхностями
|
|
4 |
Вычислить
криволинейный интеграл
|
|
5 |
Вычислить криволинейный интеграл по отрезку BC прямой, если B(–1; 0), С(0; 1). |
|
6 |
Найти координаты центра тяжести дуги циклоиды
|
|
7 |
Найти массу
первого витка винтовой линии
|
|
8 |
Определить центр тяжести однородной дуги астроиды
|
|
9 |
Вычислить
криволинейный интеграл
|
|
10 |
Вычислить
криволинейный интеграл
где l
– парабола
|
|
11 |
Вычислить
криволинейный интеграл
где l
– парабола
|
|
12 |
Вычислить
криволинейный интеграл
от
точки A(1,0)
до точки B(0,2)
по прямой
|
|
13 |
Вычислить
криволинейный интеграл
от точки A(1;
0) до точки B(0;
2) по дуге эллипса
|
|
14 |
3. Найти площадь, ограниченную кардиоидой:
|
|
15 |
Найти работу при
движении материальной точки по
окружности
|
|

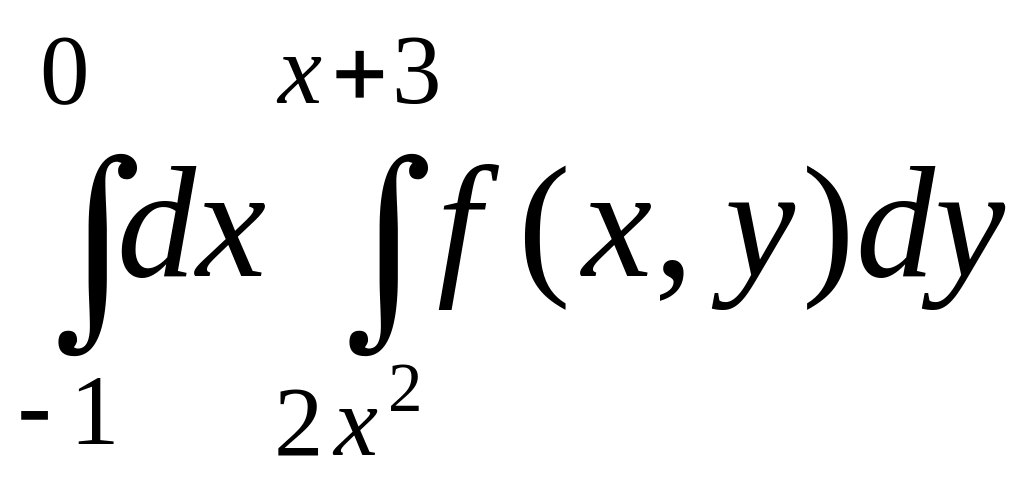 .
.