8 Дифференциальное исчисление функций нескольких переменных

8.1 Функции двух независимых переменных

Соответствие f, которое каждой паре чисел (x, y)  D сопоставляет единственное число z, называется функцией двух переменных z = f(х , y). Каждой паре чисел x, y соответствует единственная точка М(x, y) на плоскости 0xy. Функция двух переменных z = f(х, y) допускает геометрическую интерпретацию в виде поверхности в пространстве (рис. 9.1), если апликата z в точке М₀(x₀, y₀) равна значению функции f(х₀, y₀).

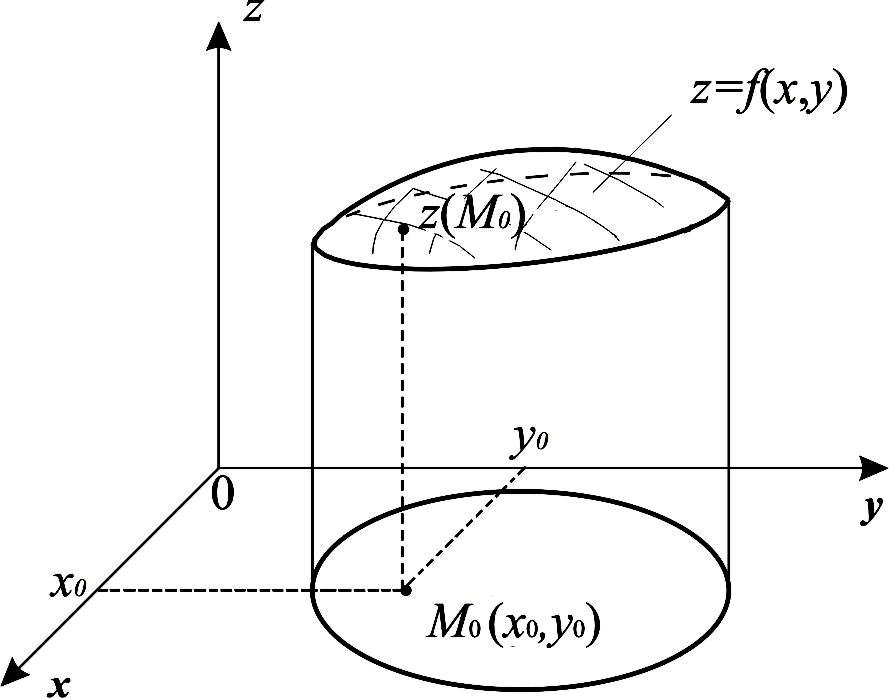
Рис. 8.1

8.2 Частные производные

Пусть z = f(х; у), тогда частные производные z¢_x, z¢_y по аргументам х и у соответственно имеют вид:

z¢_x = = ;

z¢_у = = .

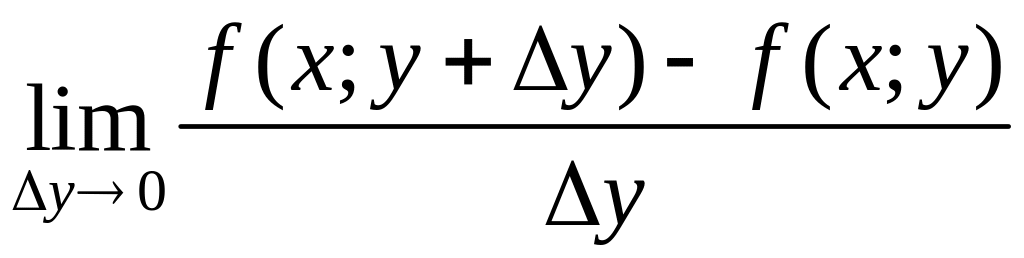Аналогично определяются частные производные функции произвольного числа аргументов. Так, например, функция трех аргументов может иметь три частные производные , , . Частные производные функции двух и более переменных находятся по формулам и правилам вычисления производных функций одной переменной (пункт 6.2); при этом все переменные, кроме той, по которой проводится дифференцирование, считаются постоянными.

Частные производные от частных производных первого порядка называются частными производными второго порядка:

.

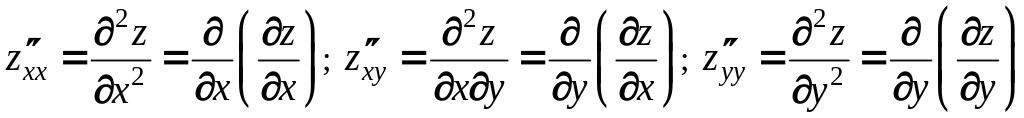Аналогично определяются и обозначаются частные производные третьего и более высоких порядков. Частные производные, взятые по различным переменным, называются смешанными производными.

Теорема (о порядке дифференцирования). Смешанные частные производные не зависят от порядка дифференцирования (в точках их непрерывности).

Например, = ; = = .

В таблице 8.1 приведены определения производных для функций одной (см. пункт 6.1) и двух переменных.

Таблица 8.1

Функция у = f(x)	Функция
Приращение:	Частные приращения: ;
Производная : у =	Частные производные : ;
Производная второго порядка	Производные второго порядка ; ;

Пример. Найти частные производные функции .

Рассматривая и как постоянные, получим

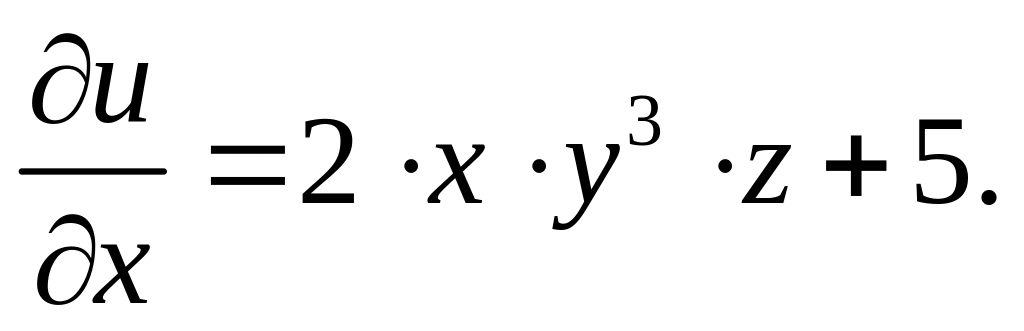
Рассматривая и как постоянные, получим

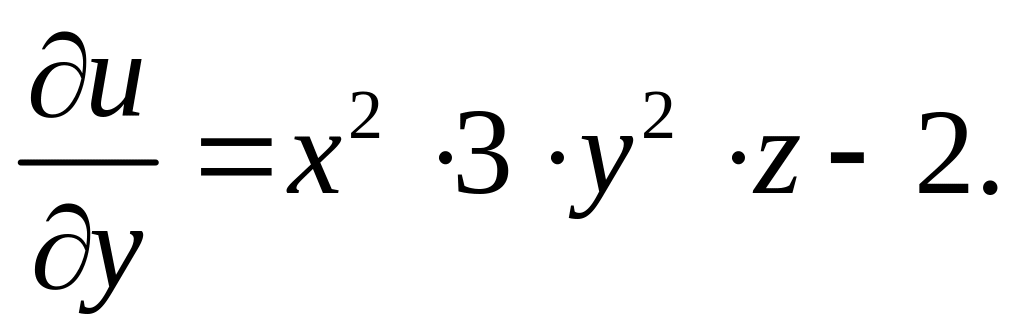
Рассматривая и как постоянные, получим

Пример. Вычислить частные производные второго порядка функции

Частные производные первого порядка:

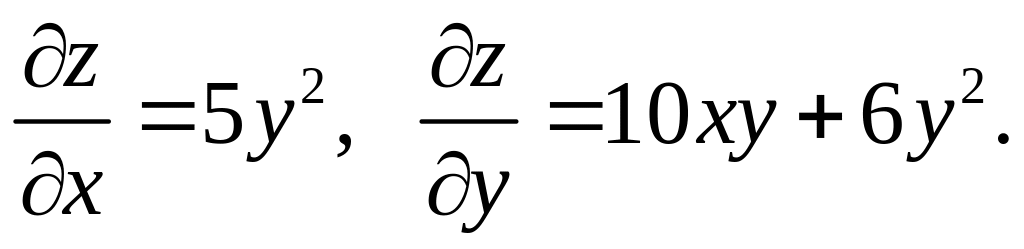
Частные производные второго порядка:

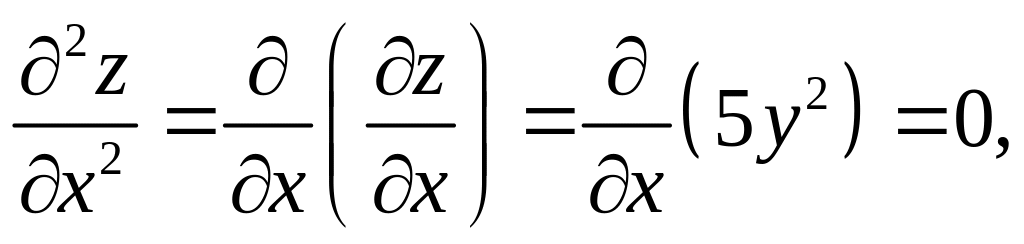
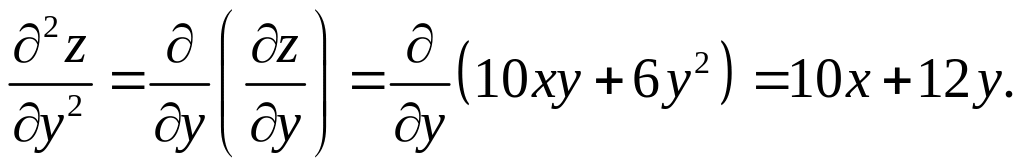
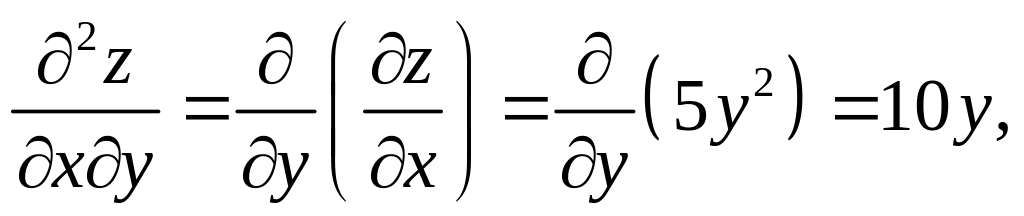
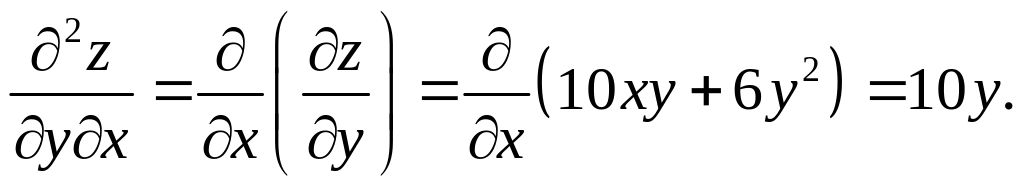
Видно, что

Пример. Найти частные производные второго порядка функции

.

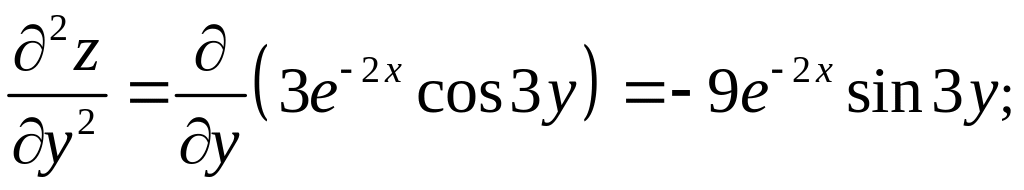
9.3 Полный дифференциал

Функция z = f(x; y) называется дифференцируемой, если ее полное приращение

z = f(x + х; y + y) – f(x; y)

может быть представлено в виде

 z = Ах + Ву +х +у,

где А, ВR, ,   0 при х, у  0.

Если функция z = f(x, y) дифференцируема в точке (x, y), то она имеет конечные частные производные в этой точке:

Определение. Полным дифференциалом функции нескольких переменных называется линейная (относительно приращения аргументов) часть приращения функции:

Замечание. x = dх, y = dy для независимых переменных.

Применение дифференциала для приближенных вычислений основано на приближенном равенстве

 .

В таблице 8.2 приведены определения дифференциалов для функций одной (см. пункт 6.5) и двух переменных.

Таблица 8.2

Функция у = f(x)	Функция
Дифференциал: dy = f (x0)x	Полный дифференциал:
Приращение функции: у  dy, f(x0 + х)   f(x0) + f¢ (x0)х	Приращение функции:

Пример. Вычислить приближенно (1,06)^2,95.

При и функция равна 1.

Производные первого порядка функции : .

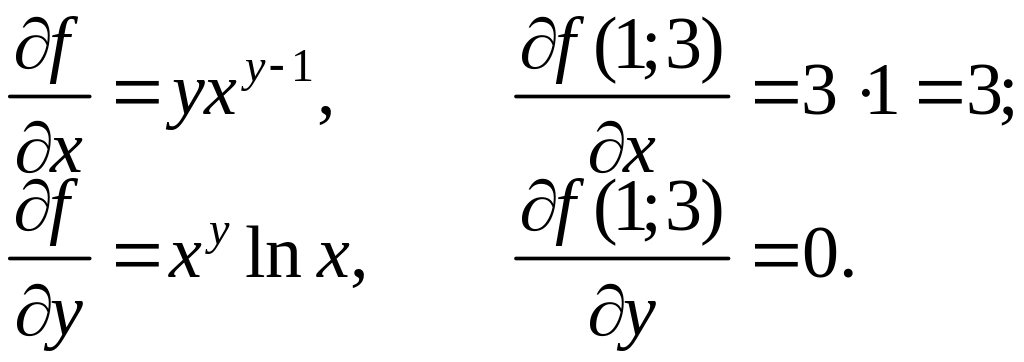Частные приращения при и :

и .

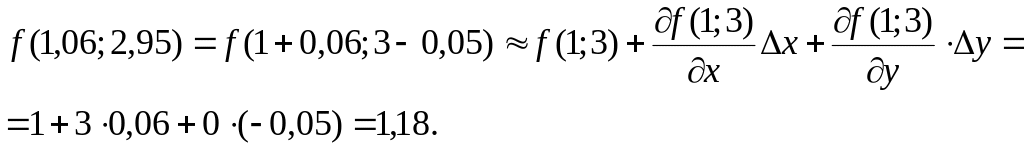
Пример. Дана функция и точки A(2;3), B(1,97;3,01). Требуется вычислить: точное значение в точке B; значение в точке A и приближенное значение в точке B; относительную погрешность приближенного значения.

1) Точное значение данной функции в точке B:

2) Значение функции в точке A:

Производные первого порядка функции :

Приближенное значение в точке B:

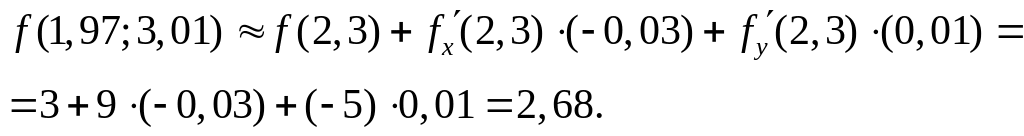
3) Абсолютная погрешность приближенного вычисления:

Относительная погрешность:

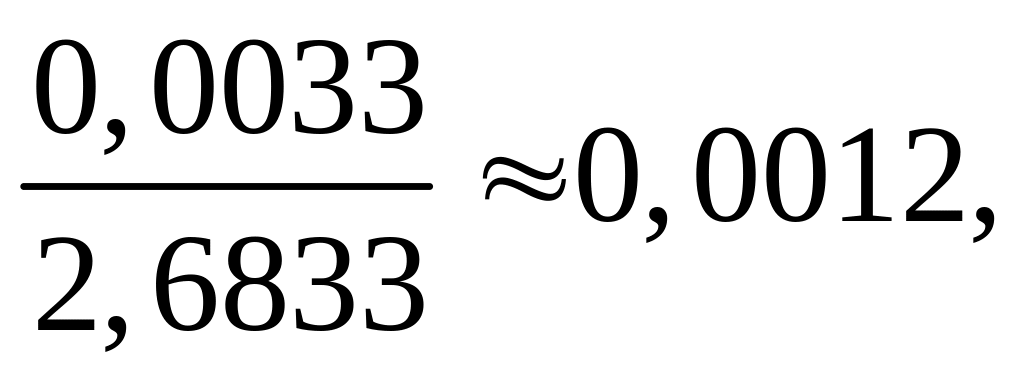
что примерно соответствует 0,1%.