9.2 Перемена порядка интегрирования

Если область D является простой, то применимы обе формулы повторного интегрирования, приведенные в предыдущем параграфе:

Иными словами, повторное интегрирование не зависит от порядка интегрирования. При вычислении двойного интеграла следует выбирать ту формулу, которая приводит к более простым выкладкам.

При изменении порядка интегрирования в повторном интеграле следует выполнить следующие действия. Начертить область интегрирования D, которая находится в полосе между прямыми и ограничена снизу линией , а сверху – линией . Затем область D надо спроектировать на ось Oy для определения прямых , ограничивающих снизу и сверху полосу, в которой расположена область D. Далее следует найти левую границу и правую области D. Если какая-либо из этих границ состоит из двух или большего числа линий, записанных разными уравнениями, то область D приходится разбивать на части, а интеграл – на сумму интегралов по этим частям.

Аналогично решается задача, если требуется изменить порядок ^{интегрирования в повторном интеграле} .

Пример. Изменить порядок интегрирования в повторном интеграле ,

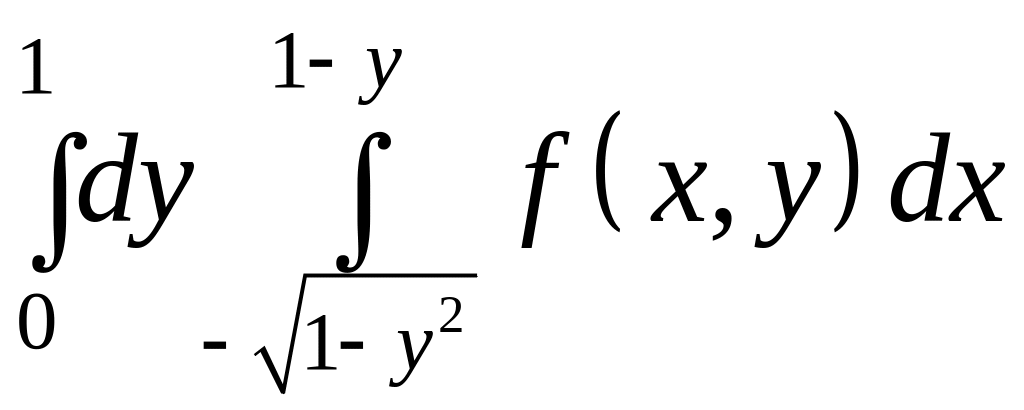График функции при 0  y  1 соответствует четверти окружности x² + y² = 1. График функции при 0  y  1 соответствует отрезку прямой y = 1 – x. Область интегрирования имеет вид

Рис. 9.1

Область такова, что при вычислении внешнего интеграла по переменной x верхняя граница области D описывается двумя уравнениями

Следовательно,

.

9.3 Вычисление площадей и объемов

Площадь S плоской области D на плоскости в прямоугольных координатах вычисляется по формуле , а в полярных координатах по формуле .

Объем V пространственной фигуры, расположенной над областью D в плоскости и ограниченной поверхностями z₁ = z₁(x; y) и z₂ = z₂(x; y) при z₁  z₂ вычисляется по формуле .

Пример. Вычислить площадь фигуры, ограниченной линиями y = x и y = 2 – x².

Найдем абсциссы точек пересечения линий, ограничивающих фигуру. Система имеет два решения x = –2 и x = 1. Значит .

Рис. 9.2

Пример. Найти площадь одного лепестка кривой .

Если полярный угол φ изменяется от 0 до π, то точка на кривой обходит против часовой стрелки один лепесток. Поэтому

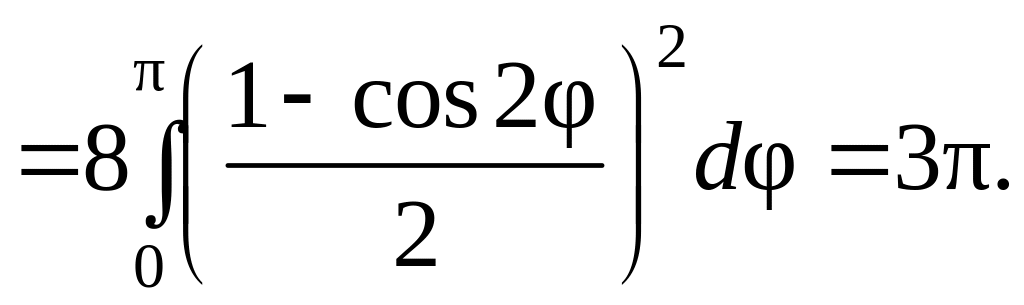
9.4 Криволинейный интеграл по длине дуги

Пусть функция непрерывна в некоторой области на плоскости , и l – некоторая кусочно-гладкая кривая, расположенная в этой области. Кусочно-гладкой кривой называется непрерывная кривая, состоящая из конечного числа гладких кусков. Кривая называется гладкой, если в каждой ее точке существует касательная, непрерывно изменяющаяся вдоль кривой.

Разобьем кривую l системой точек на элементарные дуги l₁, l₂, …, l_n. На каждой элементарной дуге l_i (i =1, 2, …, n) выберем произвольную точку и умножим значение функции в этой точке на длину элементарной дуги l_i. Сумма таких произведений по всем элементарным дугам называется интегральной суммой. Обозначим наибольшую из длин всех элементарных дуг.

Определение. Криволинейным интегралом от функции по длине дуги кривой l называется предел интегральных сумм при неограниченном увеличении числа элементарных дуг, когда все элементарные дуги стягиваются в точку:

Этот интеграл также называют криволинейным интегралом первого рода. Криволинейный интеграл по длине дуги обладает следующими свойствами:

1. , где с₁ и с₂ постоянные.

2. , если кривая l состоит из двух кривых l₁ и l₂.

3. Криволинейный интеграл по длине дуги не зависит от направления дуги интегрирования, т. е. .

При вычислении криволинейного интеграла по длине дуги возможны следующие варианты.

a) Если кривая задана уравнением y = (x), (a  x  b), то и .

b) Если кривая задана параметрически:

x = (t), y = (t), (  t  ), то и

с). если кривая задана уравнением , (₁    ₂), то и

Аналогично определяются криволинейные интегралы от непрерывной в некоторой пространственной области функции по длине дуги пространственной кусочно-гладкой кривой L, расположенной в этой области, т. е. .

Если кривая задана параметрическими уравнениями

, (  t  ), то и .