8.6 Условный экстремум
Экстремум функции
называется условным, если дополнительно
задано уравнение связи между аргументами
.
Нахождения условного экстремума
эквивалентно отысканию безусловного
экстремума функции Лагранжа:
где
–
неопределенный множитель Лагранжа.
Необходимые условия экстремума функции Лагранжа:
Обозначим
,
где
–
решение системы. Если при
выполняются неравенства
и
,
то в точке
имеет место условный максимум функции
Если при
выполняются неравенства
и
,
то в точке
имеет место условный максимум функции
Пример.
Найти экстремум функции
при условии
Функция Лагранжа:
Частные производные первого порядка функции :
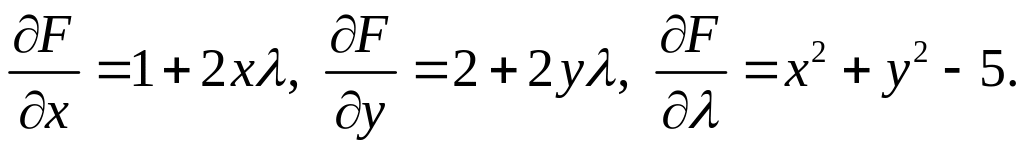
Системы
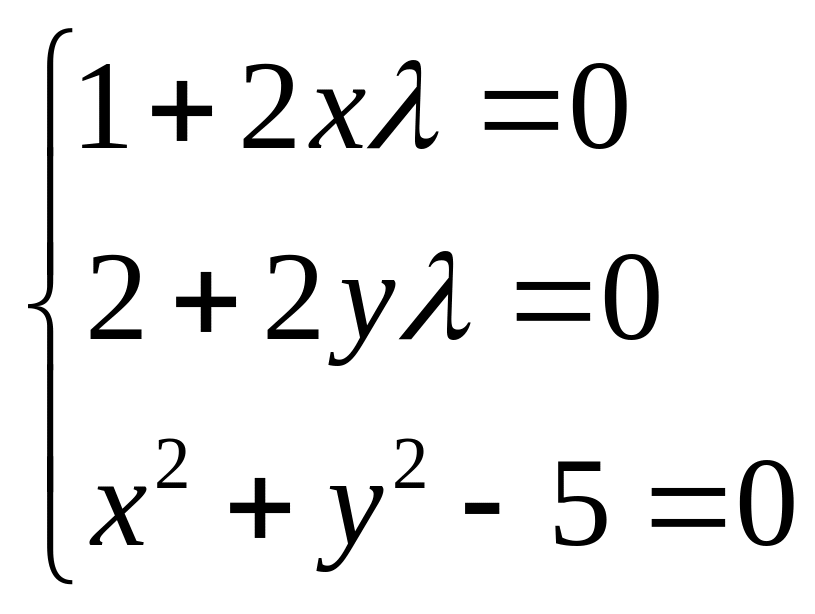имеет два решения:
и
Частные производные второго порядка функции :
Для точки (–1; –2)
при
:
А = 1 > 0,
В = 0,
С
= 1,
Следовательно,
(–1; –2)
– точка условного минимума,
Для точки (1; 2)
при
:
А = –1
< 0, В = 0,
С = –1,
Следовательно,
(–1; –2)
– точка условного максимума,
8.7 Наибольшее и наименьшее значения функции
Наибольшее и
наименьшее значения функции в ограниченной
замкнутой области достигаются либо
(безусловный экстремум) внутри области,
либо (условный экстремум) на границе
.
Условные экстремумы функции
достигаются в стационарных точках
функции Лагранжа
.
Пример.
Найти наибольшее и наименьшее значения
функции
в круге
.
Для
того чтобы найти стационарные точки
функции
,
приравниваем нулю ее частные производные.
.
Точка
(0; 0)
удовлетворяет условию
.
Стационарные точки
функции Лагранжа
можно найти, решив систему
корни
которой
и
.
В
найденных точках функция
принимает значения:
z(0, 0) = 2; z(0, 1) = 1; z(1, 0) = 3.
Следовательно, наименьшее значение функции в круге равно 1, а наибольшее – 3.
8.8 Метод наименьших квадратов
Метод наименьших
квадратов дает возможность отыскать
многочлен
,
обеспечивающий минимум среднеквадратичного
отклонения от функции
в точках
:
.
Коэффициенты
многочлена
,
обеспечивающего
минимум
,
определяются после приравнивания нулю
частных производных
функции
.
Пример. Найти
многочлен
,
приближенно заменяющий функцию
,
заданную таблично.
-
k
0
1
2
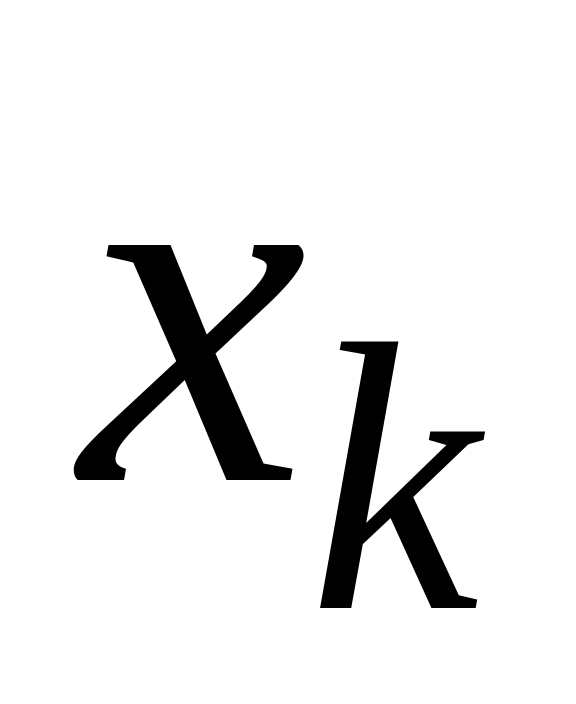
–1
0
1
5
1
0
Подсталяя
заданные значения
и
,
получаем
.
Приравнивая
частные производные функции
нулю,
составляем систему
.
Решение которой
Следовательно,
(рис. 8.3).
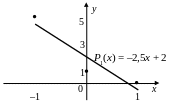
Рис. 8.3
8.9 Производная по направлению. Градиент
Математическая теория поля занимается изучением его свойств, отвлекаясь от его конкретного физического смысла. Поэтому получаемое в этой теории понятие и закономерности относятся ко всем конкретным полям. Полем называется совокупность значений той или иной величины (скорость, плотность, давление и т.п.), заданных в каждой точке рассматриваемой области. Поле называется скалярным (векторным), если рассматриваемая величина скаляр (вектор). Если значения рассматриваемых величин не изменяются во времени, то поле называется стационарным (установившимся), если же они изменяются во времени, то поле называется нестационарным.
Функция u = f(х, y, z), заданная в области V пространства 0xyz (или функция u = f(х, y,), заданная в области V плоскости 0xy), определяет в этой области скалярное поле. Поверхностью (линией) уровня пространственного (плоского) поля, называется множество точек, в которых поле принимает одинаковое значение.
Для функция
f(х, у, z),
имеющей частные производные в
точке М0(x0, y0, z0),
производная
по направлению
вычисляется по формуле
где cos
=
,
cos
=
,
cos
=
– направляющие косинусы (см. пункт 2.1)
вектора
.
Производная
по направлению
характеризует скорость изменения
скалярного поля в точке М0
в направлении
.
Градиентом скалярного поля называется вектор
gradu
=
+
+
.
Вектор gradu
направлен в сторону наискорейшего
возрастания функции u = f(х0; y0 ; z0)
в данной точке и совпадает с направлением
перпендикуляра к поверхности (линии)
уровня. Связь между
и gradu
устанавливается формулой
= gradu 
,
где
– орт (см. пункт 2.1) вектора
(рис.
8.4).
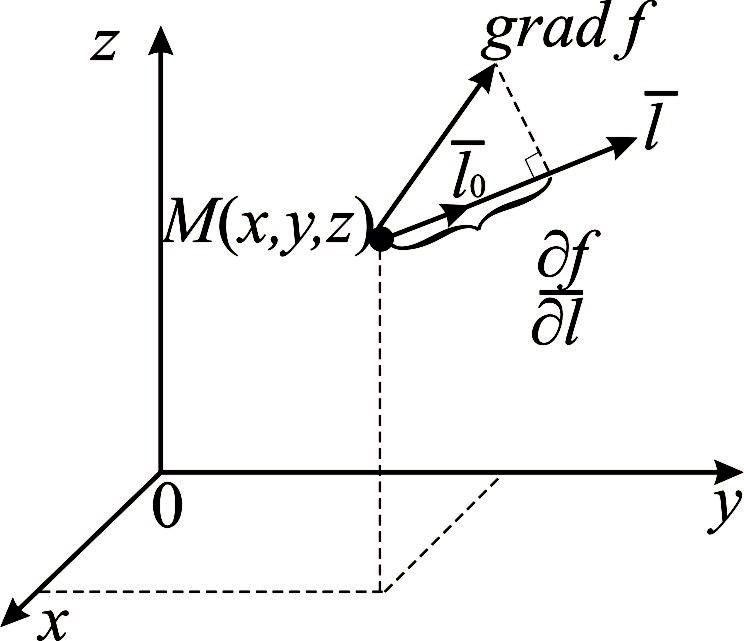
Рис. 8.4
Пример.
Установить, какой график (рис. 8.5)
соответствует линии уровня плоского
поля
.
|
|
|
Рис. 8.5
Линией уровня
является окружность
,
изображенная на рисунке II.
Пример. Найти градиент скалярного поля u = xy + 2z – z2 в точке
М(1; 1; 0).
gradu
=
+
+
= y
+ x
+ (2 – 2z)
;
gradМu
=
+
+ 2
.
Пример.
Найти градиент и производную скалярного
поля u
= x2
+ 3xy2
в точке М(1;
1) в направлении
единичного вектора
=
(0; 1).
;
.
,
gradМ
u
=
= 5
+ 6
.
= gradМ
u
= (5
+ 6
)
= 6.
Замечание. Производную по направлению можно вычислить по формуле
.