
- •Часть II
- •8 Дифференциальное исчисление функций нескольких переменных
- •8.1 Функции двух независимых переменных
- •8.2 Частные производные
- •9.3 Полный дифференциал
- •8.4 Касательная плоскость и нормаль к поверхности
- •8.5 Экстремумы функций двух переменных
- •8.6 Условный экстремум
- •8.7 Наибольшее и наименьшее значения функции
- •8.8 Метод наименьших квадратов
- •8.9 Производная по направлению. Градиент
- •Задачи для самостоятельного решения
- •9 Кратные, криволинейные и поверхностные интегралы. Элементы теории поля
- •9.1 Двойной интеграл
- •9.2 Перемена порядка интегрирования
- •9.3 Вычисление площадей и объемов
- •9.4 Криволинейный интеграл по длине дуги
- •9.5 Геометрические и механические приложения криволинейного интеграла по длине дуги
- •9.5 Криволинейный интеграл по координатам
- •9.6 Формула Грина-Остроградского
- •9.7 Независимость криволинейного интеграла 2-го рода от формы дуги кривой
- •9.8 Геометрические и механические приложения криволинейных интегралов 2-го рода
- •Задачи для самостоятельного решения
- •10 Ряды. Гармонический анализ
- •10.1 Числовые ряды
- •10.2 Степенные ряды
- •10.3 Ряды Тейлора и Маклорена
- •10.4 Тригонометрические ряды Фурье
- •Задачи для самостоятельного решения
- •11 Дифференциальные уравнения
- •11.1 Дифференциальные уравнения первого порядка
- •11.2 Основные типы уравнений первого порядка
- •11.3 Понижение порядка уравнения
- •11.4 Линейные уравнения с постоянными коэффициентами
- •12 Операционное исчисление. Уравнения математической физики
- •12.1 Оригиналы и изображения
- •12.2 Теоремы операционного исчисления
- •12.3 Таблица изображений
- •12.4 Свёртка функций
- •12.5 Нахождение оригинала по изображению
- •12.6 Операционный метод решения дифференциальных уравнений с постоянными коэффициентами. Методы решения уравнений математической физики
- •12.7 Решение систем линейных дифференциальных уравнений с постоянными коэффициентами
- •Задачи для самостоятельного решения
- •13 Теория вероятностей
- •13.1 Классическое определение вероятности
- •Основные свойства вероятности
- •13.2 Теоремы умножения и сложения вероятностей
- •13.3 Формула полной вероятности. Формула Байеса
- •13.4 Схема Бернулли
- •13.5 Функция и плотность распределения вероятностей
- •13.6 Свойства функции и плотности распределения вероятностей
- •13.7 Числовые характеристики случайных величин
- •13.8 Свойства математического ожидания и дисперсии
- •13.9 Основные законы распределения вероятностей случайных величин
- •13.10 Связь между случайными величинами
- •Задачи для самостоятельного решения
- •14 Математическая статистика
- •14.1 Эмпирическая функция распределения. Гистограмма
- •14.2 Точечные и интервальные оценки параметров
- •14.3 Статистические гипотезы
- •Задачи для самостоятельного решения
- •Приложение а. Таблица значений функции Лапласа ф0(х)
- •Приложение б. Основные математические обозначения
14.2 Точечные и интервальные оценки параметров
Точечной оценкой
(оценкой одним числом) неизвестного
параметра
генеральной совокупности является
число, зависящее от элементов выборки.
Точечными оценками математического
ожидания и дисперсии генеральной
совокупности Х
являются
выборочное
среднее
![]() и выборочная
дисперсия
и выборочная
дисперсия
![]() или исправленная выборочная дисперсия
или исправленная выборочная дисперсия
![]() .
.
Интервальной оценкой неизвестного параметра генеральной совокупности называется интервал (* – , * + ), накрывающий неизвестное значение оцениваемого параметра с заданной вероятностью , которую называют доверительной вероятностью (рис. 14.3):
![]() .
.
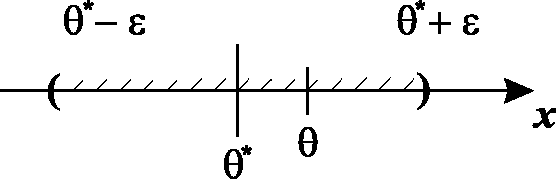
Рис. 14.3
Интервал (* – , * + ) называется доверительным интервалом, – точностью оценки.
Пример. Результаты измерений, полученных при испытаниях: 4; 5; 8; 9; 11. Найти оценку математического ожидания.
![]() = 7,4.
= 7,4.
Пример. Результаты измерений, полученных при испытаниях: 11; 13; 15. Найти оценку дисперсии s2.
Математическое
ожидание
![]() (11
+ 13 + 15) = 13;
(11
+ 13 + 15) = 13;
исправленная
выборочная дисперсия
s2 = ![]() = 4.
= 4.
Пример. Точечная оценка параметра распределения равна 20. Какой из интервалов (20; 21), (19; 21), (0, 20), (19, 20) может служить интервальной оценкой?
Интервальной оценкой (* – , * + ) является интервал (19; 21) при * = 20 и = 1.
14.3 Статистические гипотезы
Статистической называют гипотезу о параметрах генеральной совокупности или о виде ее распределения. Например, статистическими являются гипотезы:
1) генеральная совокупность распределена по нормальному закону;
2) дисперсии двух генеральных совокупностей равны между собой.
В первой гипотезе сделано предположение о виде неизвестного распределения, во второй – параметрах двух распределений.
Выдвинутая гипотеза
![]() называется
нулевой
(основной). Альтернативной
(конкурирующей)
называется гипотеза
называется
нулевой
(основной). Альтернативной
(конкурирующей)
называется гипотеза
![]() ,
которая противоречит нулевой. Например,
если проверяется основная гипотеза
о нулевом значении математического
ожидания (
,
которая противоречит нулевой. Например,
если проверяется основная гипотеза
о нулевом значении математического
ожидания (![]() ),
то предположение
),
то предположение
![]() может быть альтернативной гипотезой
,
может быть альтернативной гипотезой
,
Выдвинутая гипотеза
может быть ошибочной, поэтому возникает
необходимость ее статистической
проверки, т.е. непротиворечивости
гипотезы
и результатов опытов. После статистической
проверки гипотеза может быть либо
принята, либо отвергнута. Для проверки
гипотезы
используют специально подобранную
случайную величину
![]() ,
распределение которой известно. Величина
,
обеспечивающая проверку гипотезы
,
называется статистическим
критерием.
Критической областью
называется
множество значений критерия
,
при которых нулевая гипотеза
отвергается. Эта область должна быть
выбрана так, чтобы попадание в нее
случайной величины
было событием маловероятным, если
гипотеза
верна. Значение критерия, вычисленное
по выборке, называется наблюдаемым
значением
,
распределение которой известно. Величина
,
обеспечивающая проверку гипотезы
,
называется статистическим
критерием.
Критической областью
называется
множество значений критерия
,
при которых нулевая гипотеза
отвергается. Эта область должна быть
выбрана так, чтобы попадание в нее
случайной величины
было событием маловероятным, если
гипотеза
верна. Значение критерия, вычисленное
по выборке, называется наблюдаемым
значением
![]() .
Если эта величина оказалась в критической
области, то считается, что выдвинутое
предположение не согласуется с конкретной
выборкой. В этом случае гипотеза
признается ошибочной.
.
Если эта величина оказалась в критической
области, то считается, что выдвинутое
предположение не согласуется с конкретной
выборкой. В этом случае гипотеза
признается ошибочной.
Принятое
статистическое решение не всегда бывает
верным. Ошибка
первого рода
состоит в том, что отвергнута правильная
гипотеза
(предположение отвергнуто, хотя оно
верно). Ошибка
второго рода
состоит в том, что принята неправильная
гипотеза
(предположение признано верным, хотя
оно ошибочно). Вероятность
![]() совершения ошибки первого рода называется
уровнем
значимости критерия.
совершения ошибки первого рода называется
уровнем
значимости критерия.
