13.6 Свойства функции и плотности распределения вероятностей

1) Р(а  Х < b) = F(a) – F(b) = . Вероятность попадания случайной величины Х в интервал [a; b) равна площади заштрихованной криволинейной трапеции (рис. 13.3).

2) Для непрерывной случайной величины Р(х = а) = Р(х = b) = 0, следовательно, Р(а  Х < b) = Р(а < Х < b) = Р(а  Х  b).

3) .

4) .

5) неубывающая функция.

6) f(х)  0.

7) F(х) = .

8) = 1. Площадь S, заключенная между графиком плотности распределения f(х) и осью 0х, равна единице (рис. 13.2).

Рис. 13.3

Пример. Дискретная случайная величина задана законом распределения

xi	–1	2	4
pi	0,1	0,5	0,4	.

Вычислить функцию распределения F(x) при х = 2,4.

.

Пример. Функция распределения случайной величины Х имеет вид:

при х < 0; при х [0; 2]; при х > 2.

Найти вероятность того, что случайная величина примет значение из интервала ([1; 1,5), и плотность распределения f(х).

Р(1 < х < 1,5) = F(1,5) – F(1) = .

при х < 0; при х [0; 2]; при х > 2.

13.7 Числовые характеристики случайных величин

Математическое ожидание МХ – величина, около которой группируются возможные значения случайной величины (числовая характеристика положения); дисперсия DХ характеризует рассеивание (отклонение) случайной величины относительно её математического ожидания.

Для дискретной случайной величины математическое ожидание и дисперсия вычисляются по формулам

МХ = , DХ = .

Для непрерывной случайной величины

МХ = , DХ = .

Размерность величины МХ совпадает с размерностью самой случайной величины Х, а размерность DХ равна квадрату размерности Х. Поэтому в качестве числовой характеристики рассеивания используется также среднеквадратичное отклонение .

Мода во множестве наблюдений, значение которое встречается наиболее часто. Иногда в совокупности встречается более чем одна мода. Например, мода равна 6 и 9, если зафиксированы значения 2, 6, 6, 6, 8, 9, 9, 9, 10.

Мода дискретной случайной величины – любое её значение, имеющее вероятность, равную максимальной вероятности

Рис. 13.5

Модой М₀ непрерывной случайной величины называется точка максимума ее плотности распределения. Медианой М_е непрерывной случайной величины Х называется такое ее значение, что вероятности попадания Х левее и правее медианы равны (рис 13.4), т.е.

P(X < М_е) = P(X  М_е) =  .

Рис. 13.4

Пример. Дискретная случайная величина задана законом распределения

xi	–1	2	4
pi	0,1	р2	р3	.

Найти вероятности р₂, р₃, если математическое ожидание случайной величины равно 3,3.

 



Пример. Найти математическое ожидание случайной величины Х, график функции распределения F(х) которой представлен на рисунке 13.4.

Рис. 13.6

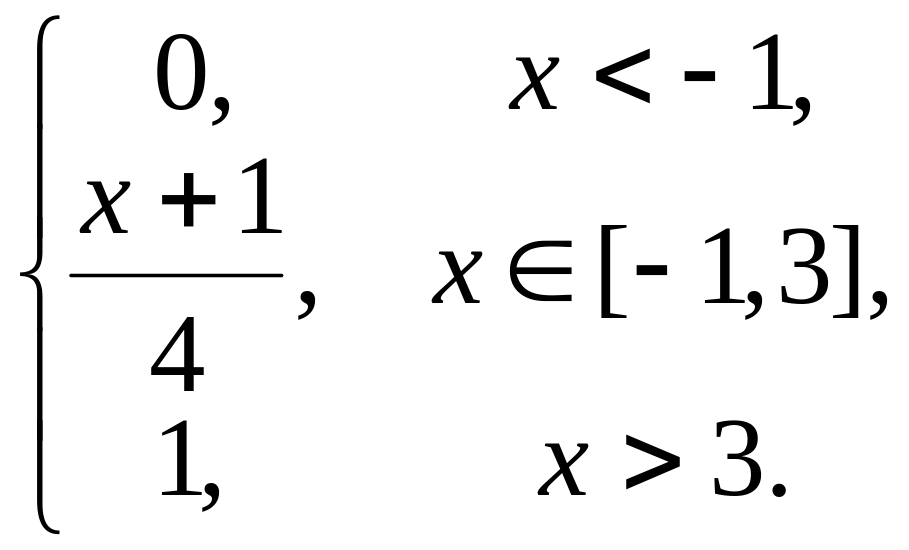
F(х) =  f(х) = F ¢(х) =

МХ =   =   =  = = 1.