13.3 Формула полной вероятности. Формула Байеса

Если событие А может произойти только вместе с одним из событий Н_i (единственно возможных, попарно несовместных), то вероятность события А (доопытная, априорная) находится по формуле полной вероятности:

Р(А) = .

Если событие А произошло, то послеопытная (апостериорная) вероятность события Н_i определяется по формуле Байеса:

Р(Н_i/А) = = .

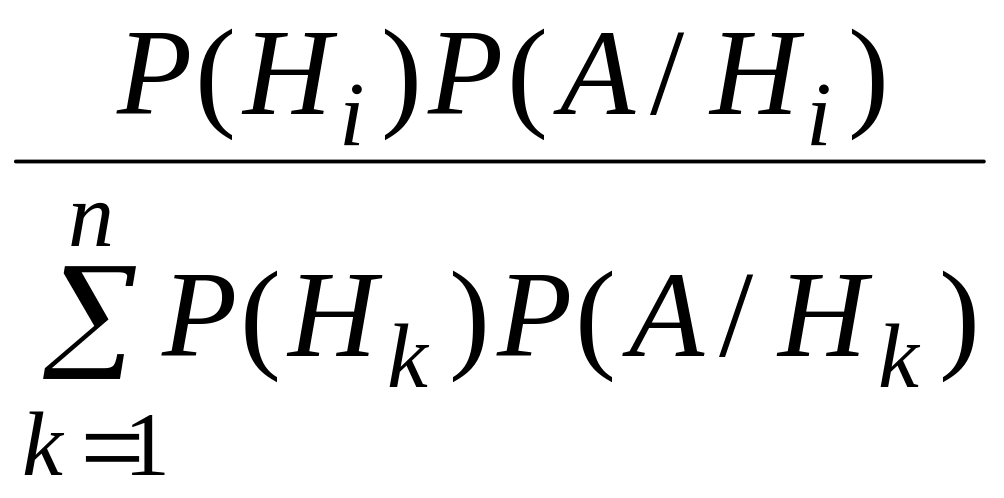Пример. В первой урне 3 белых и 7 чёрных шаров. Во второй урне 5 белых и 15 чёрных шаров. Найти вероятность того, что

1) шар, извлечённый из наудачу выбранной урны, будет белый;

2) извлечённый белый шар находился во второй урне.

Обозначим

А = {извлечён белый шар},

Н₁ = {выбрана 1-я урна},

Н₂ = {выбрана 2-я урна}.

1) Р(Н₁) = Р(Н₂) = , Р(А/Н₁) = , Р(А/Н₂) = .

Р(А) = Р(Н₁)Р(А/Н₁) + Р(Н₂)Р(А/Н₂) = .

2) Р(Н₂/А) = .

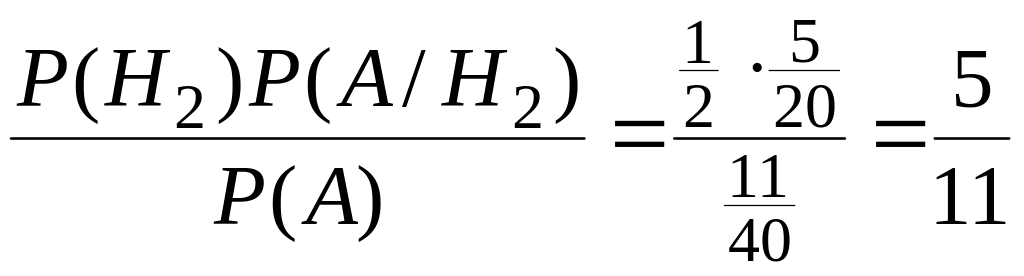13.4 Схема Бернулли

Испытания называются независимыми, если вероятность события А в каждом испытании не зависит от исходов других испытаний. Схема Бернулли – последовательность n независимых испытаний, в каждом из которых событие А может либо произойти («успех»), либо не произойти («неудача»). Вероятность «успеха» в испытаниях не меняется: Р(А) = р, . Обозначим _n – число «успехов» в серии n испытаний (0  _n  n). Вероятность того, что в испытаниях произойдет m «успехов» вычисляется по формуле Бернулли:

Р(_n = m) = ; 0  m  n,

где − число сочетаний по m элементов из n (количество комбинаций, различающихся составом m элементов, выбранных из n элементов).

Вероятность того, что в n испытаниях произойдет от m₁ до m₂ «успехов» (0  m₁  m₂  n):

Р(m₁  _n  m₂) = .

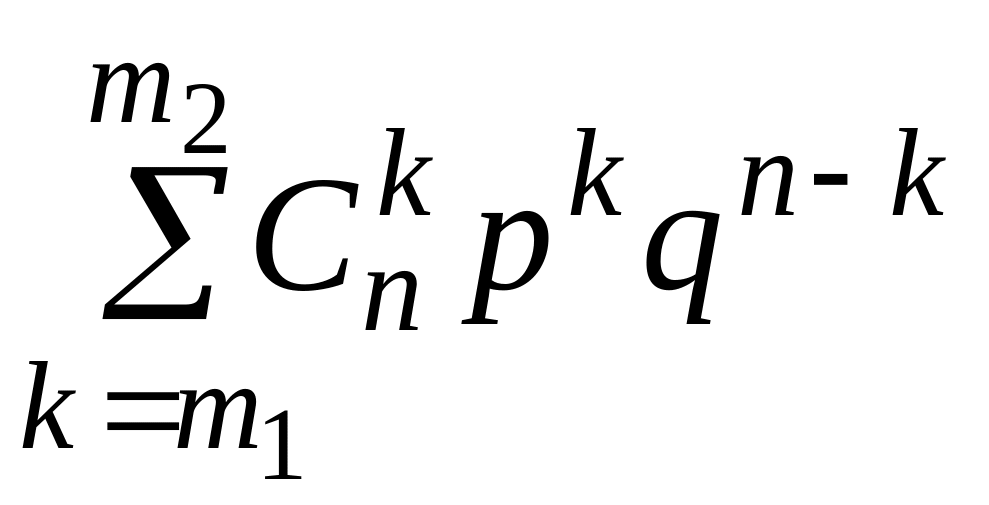Пример. В мишень стреляют четыре раза. Вероятность поражения при одном выстреле 0,8. Определить вероятность того, что мишень будет поражена ровно два раза.

р = 0,8; q = 0,2; n = 4; m = 2. .

Пример. В мишень стреляют четыре раза. Вероятность поражения при одном выстреле 0,8. Определить вероятность того, что мишень будет поражена хотя бы один раз.

р = 0,8; q = 0,2; n = 4; m₁ = 1; m₂ = 4.

= 1−P ( =0) = .

13.5 Функция и плотность распределения вероятностей

Случайной величиной Х называется переменная величина, принимающая в результате испытания одно из множества возможных значений.

Случайная величина х называется дискретной, если она принимает конечное или счетное множество значений. Дискретная случайная величина задается законом распределения, т. е. множеством пар (x_i; p_i), где х_i – возможные значения случайной величины, p_i – вероятности принятия случайной величиной значений x_i. При этом . Соответствие p_i и х_i называется законом распределения дискретной случайной величины:

Таблица 13.1

хi	х1	х2	х3	…	хn
рi	р1	р2	р3	…	рn

Неслучайную величину С можно рассматривать как случайную с законом распределения

Таблица 13.2

хi	С
рi	1

Функция распределения дискретной случайной величины определяется формулой

,

где суммируются вероятности тех значений x_i, которые меньше x.

Непрерывная случайная величина может принимать все значения из некоторого (конечного или бесконечного) промежутка. Функция распределения непрерывной случайной величины определяется формулой

F(х) = Р(Х < х).

Если функция F(х) дифференцируема, то ее производная f(х) = F (х) называется плотностью распределения вероятностей.