- •Часть II
- •8 Дифференциальное исчисление функций нескольких переменных
- •8.1 Функции двух независимых переменных
- •8.2 Частные производные
- •9.3 Полный дифференциал
- •8.4 Касательная плоскость и нормаль к поверхности
- •8.5 Экстремумы функций двух переменных
- •8.6 Условный экстремум
- •8.7 Наибольшее и наименьшее значения функции
- •8.8 Метод наименьших квадратов
- •8.9 Производная по направлению. Градиент
- •Задачи для самостоятельного решения
- •9 Кратные, криволинейные и поверхностные интегралы. Элементы теории поля
- •9.1 Двойной интеграл
- •9.2 Перемена порядка интегрирования
- •9.3 Вычисление площадей и объемов
- •9.4 Криволинейный интеграл по длине дуги
- •9.5 Геометрические и механические приложения криволинейного интеграла по длине дуги
- •9.5 Криволинейный интеграл по координатам
- •9.6 Формула Грина-Остроградского
- •9.7 Независимость криволинейного интеграла 2-го рода от формы дуги кривой
- •9.8 Геометрические и механические приложения криволинейных интегралов 2-го рода
- •Задачи для самостоятельного решения
- •10 Ряды. Гармонический анализ
- •10.1 Числовые ряды
- •10.2 Степенные ряды
- •10.3 Ряды Тейлора и Маклорена
- •10.4 Тригонометрические ряды Фурье
- •Задачи для самостоятельного решения
- •11 Дифференциальные уравнения
- •11.1 Дифференциальные уравнения первого порядка
- •11.2 Основные типы уравнений первого порядка
- •11.3 Понижение порядка уравнения
- •11.4 Линейные уравнения с постоянными коэффициентами
- •12 Операционное исчисление. Уравнения математической физики
- •12.1 Оригиналы и изображения
- •12.2 Теоремы операционного исчисления
- •12.3 Таблица изображений
- •12.4 Свёртка функций
- •12.5 Нахождение оригинала по изображению
- •12.6 Операционный метод решения дифференциальных уравнений с постоянными коэффициентами. Методы решения уравнений математической физики
- •12.7 Решение систем линейных дифференциальных уравнений с постоянными коэффициентами
- •Задачи для самостоятельного решения
- •13 Теория вероятностей
- •13.1 Классическое определение вероятности
- •Основные свойства вероятности
- •13.2 Теоремы умножения и сложения вероятностей
- •13.3 Формула полной вероятности. Формула Байеса
- •13.4 Схема Бернулли
- •13.5 Функция и плотность распределения вероятностей
- •13.6 Свойства функции и плотности распределения вероятностей
- •13.7 Числовые характеристики случайных величин
- •13.8 Свойства математического ожидания и дисперсии
- •13.9 Основные законы распределения вероятностей случайных величин
- •13.10 Связь между случайными величинами
- •Задачи для самостоятельного решения
- •14 Математическая статистика
- •14.1 Эмпирическая функция распределения. Гистограмма
- •14.2 Точечные и интервальные оценки параметров
- •14.3 Статистические гипотезы
- •Задачи для самостоятельного решения
- •Приложение а. Таблица значений функции Лапласа ф0(х)
- •Приложение б. Основные математические обозначения
12.3 Таблица изображений
В таблице 12.1 приведены изображения часто встречающихся на практике функций.
Таблица 12.1
-
№
Оригинал
Изображение
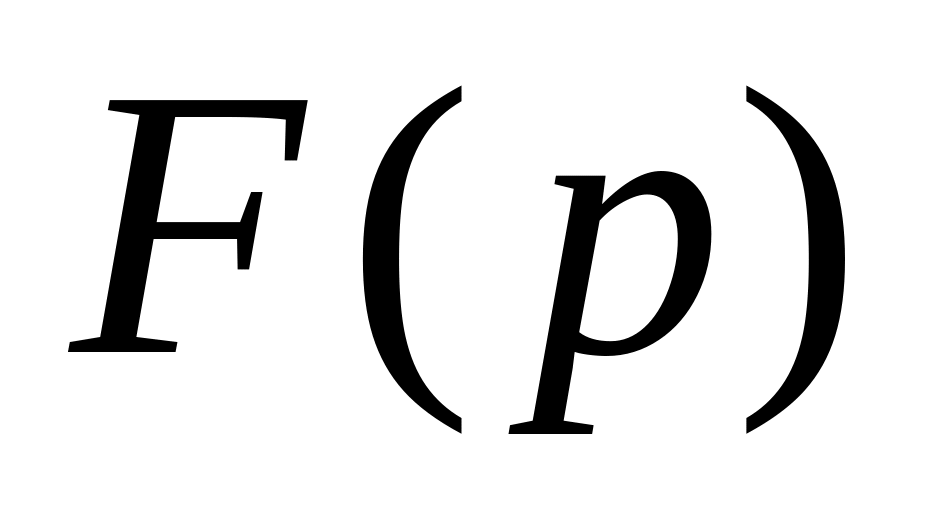
№
Оригинал
Изображение
1
1(t)

9
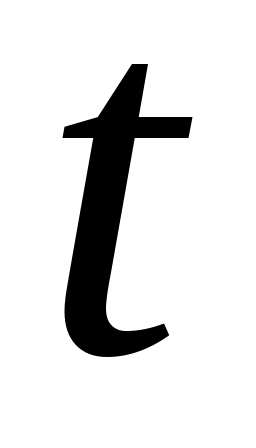
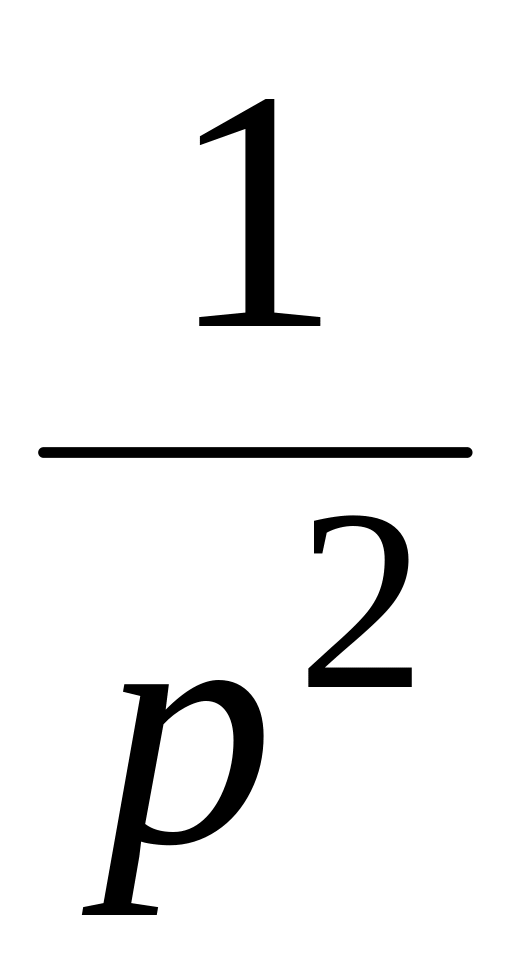
2
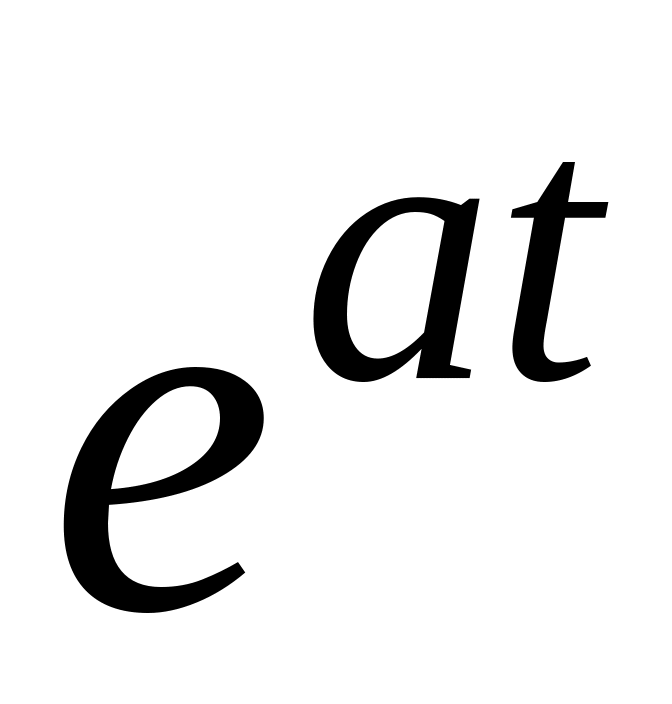
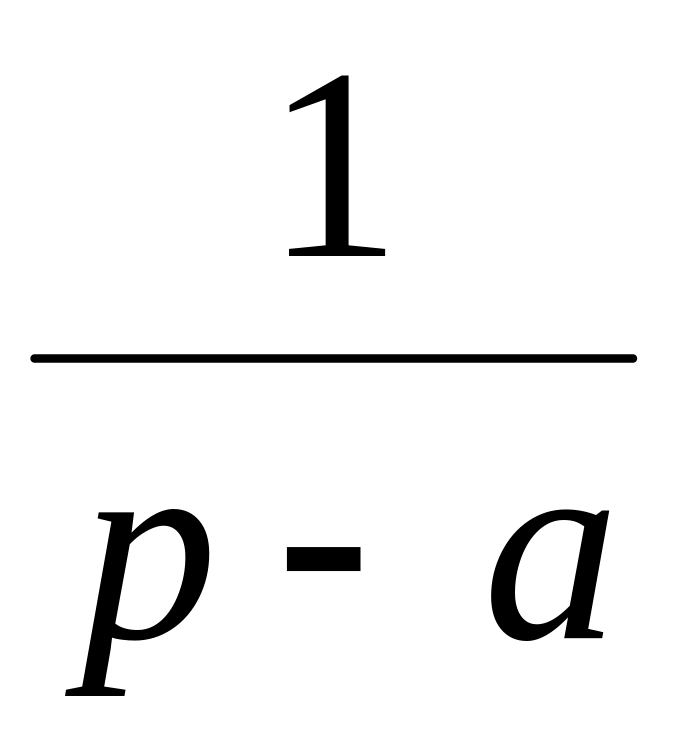
10
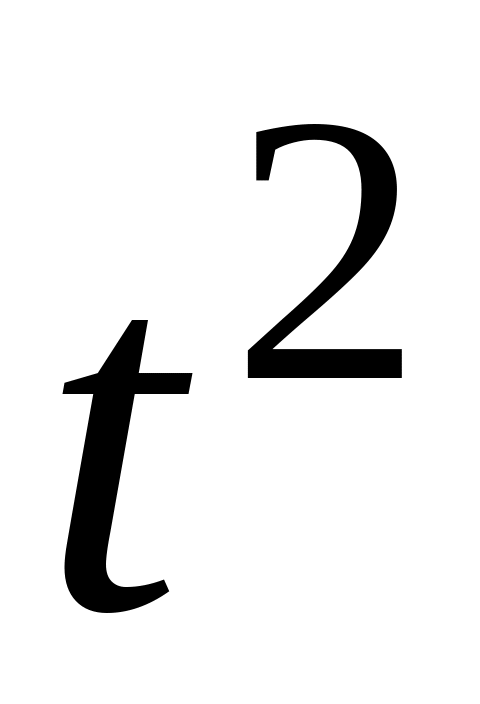
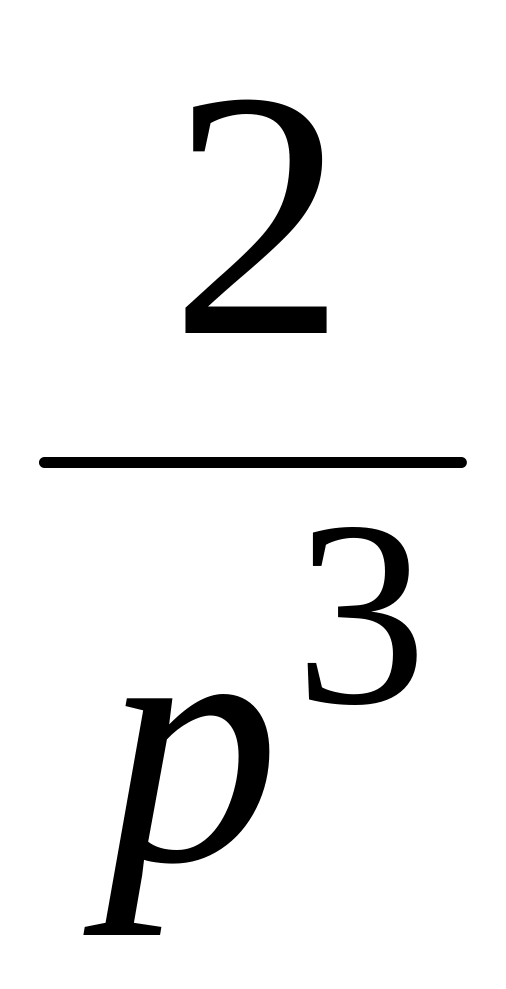
3
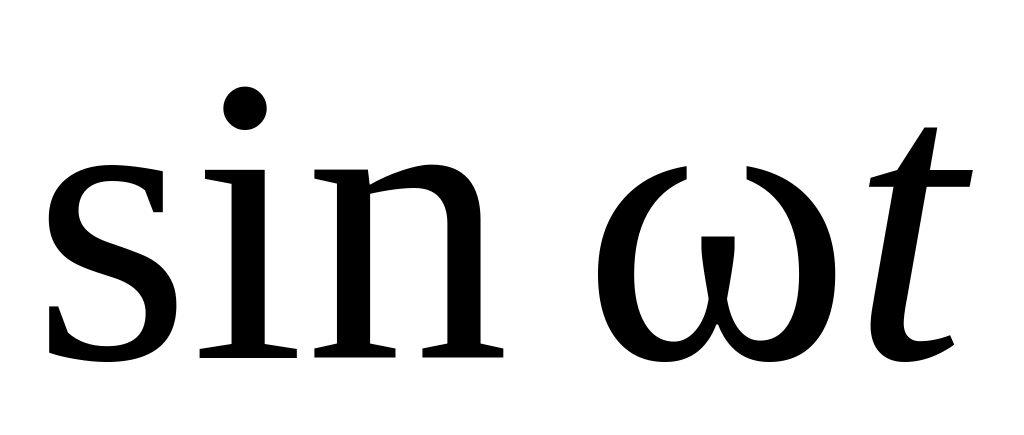
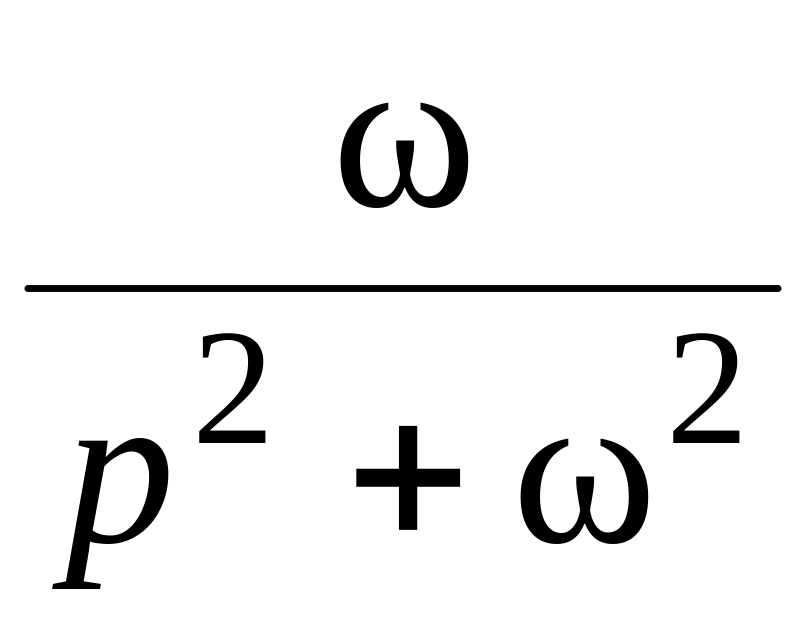
11
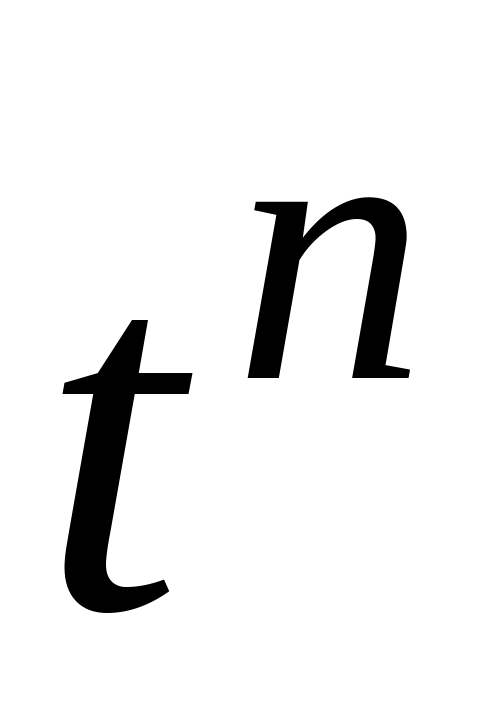
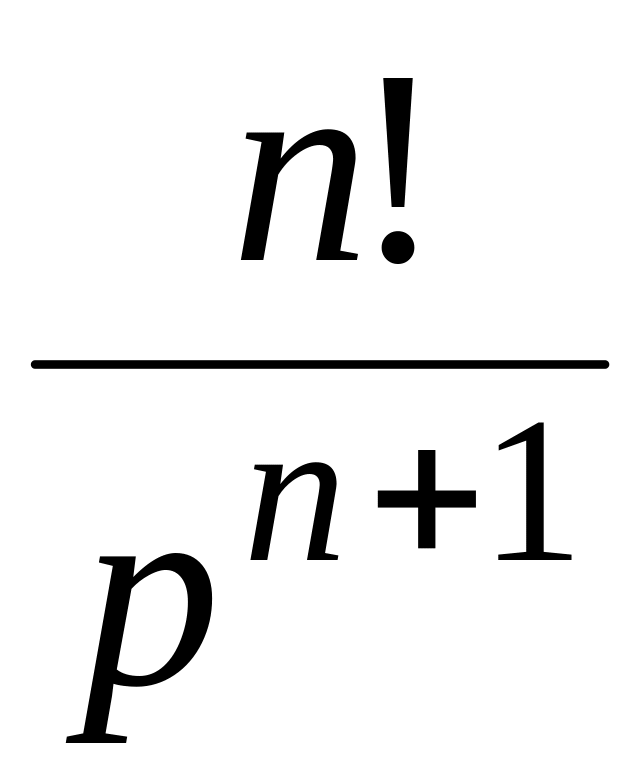
4
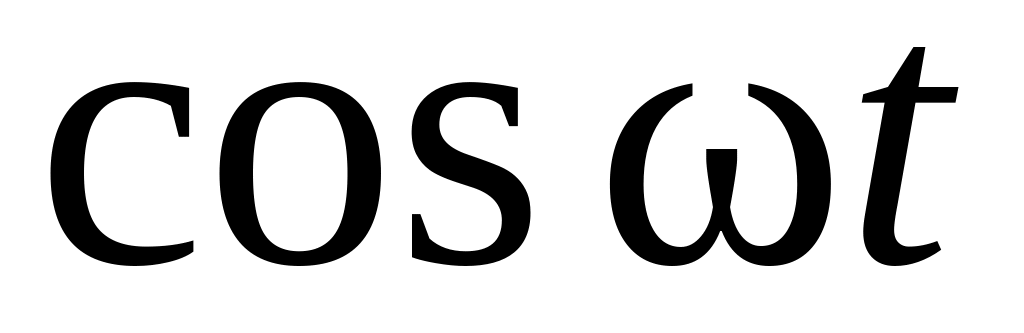
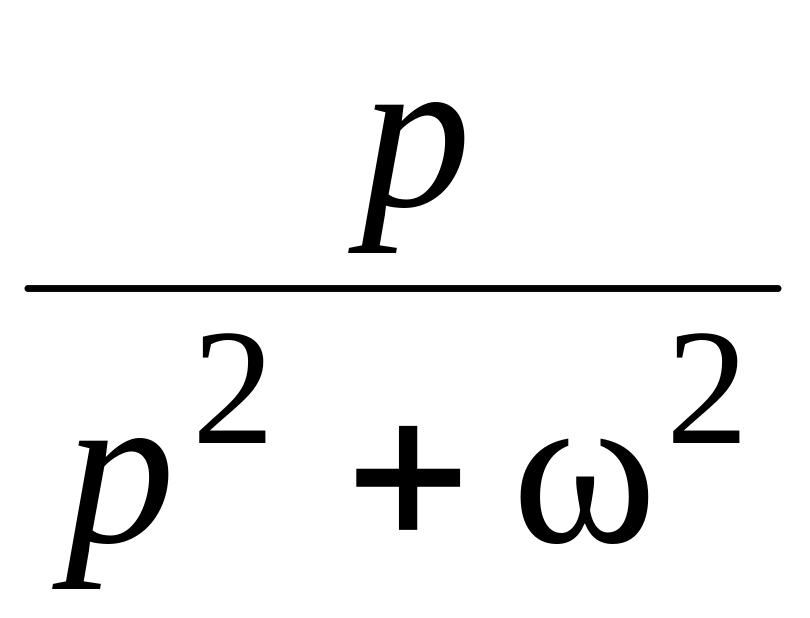
12
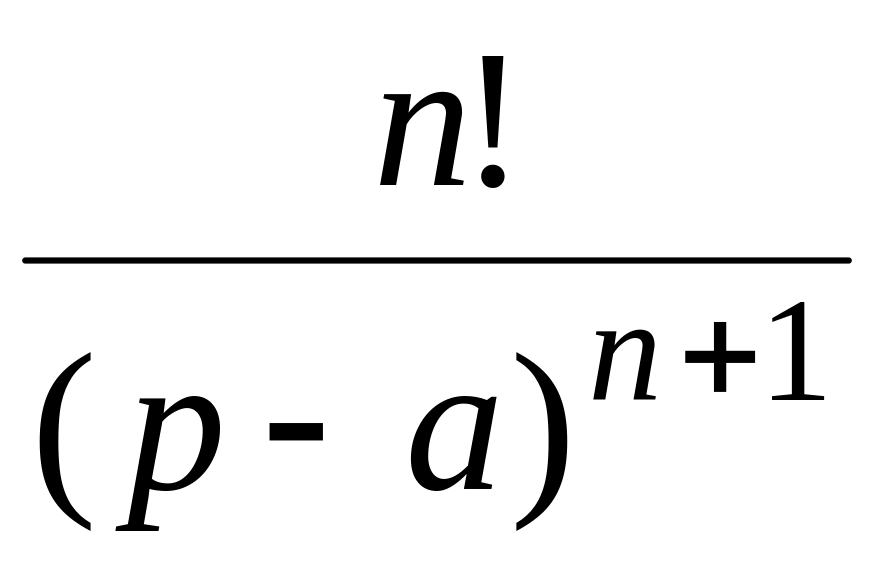
5
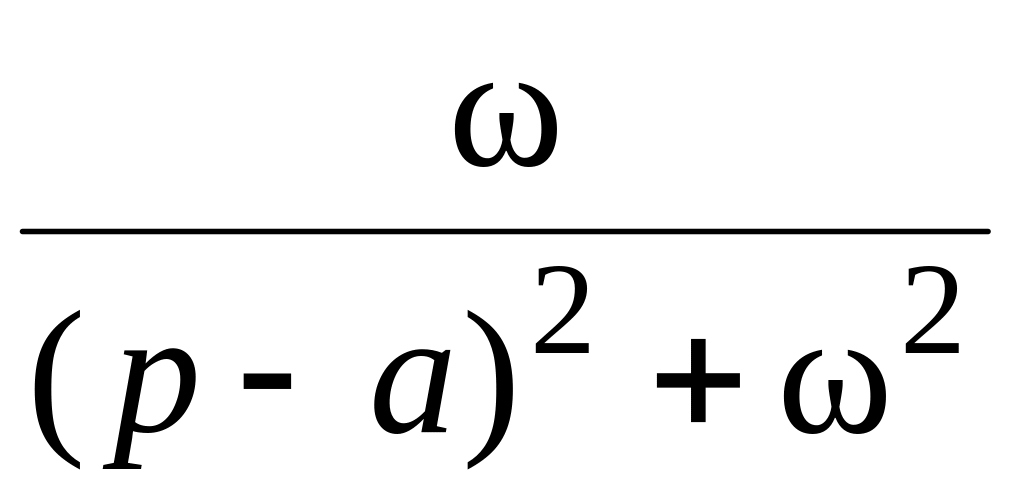
13
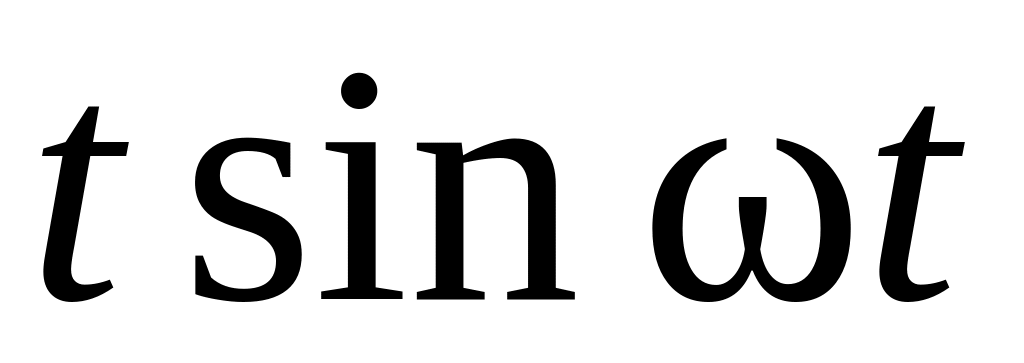
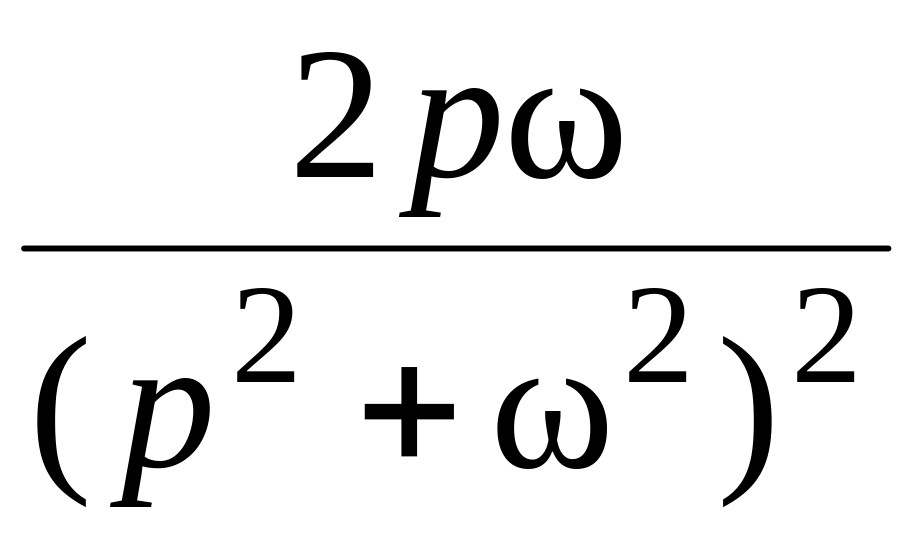
6
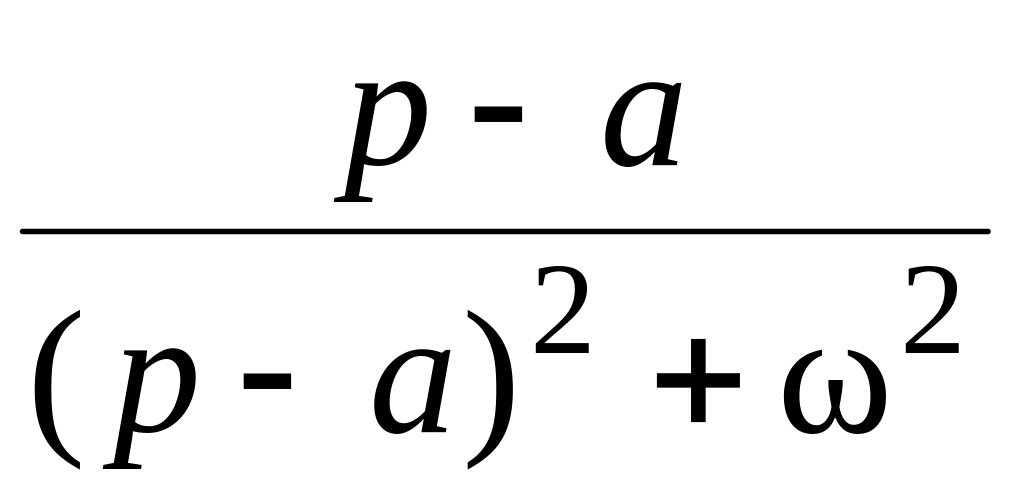
14


7
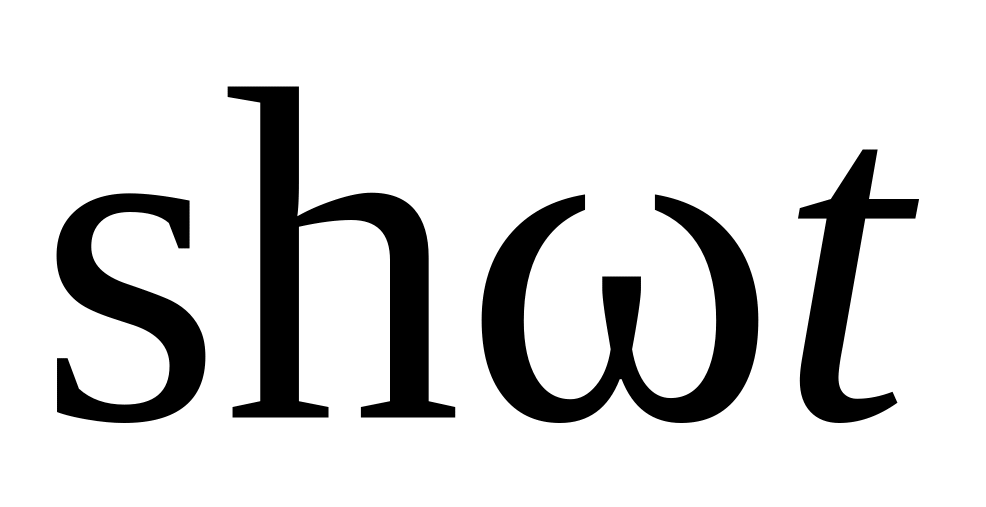

15
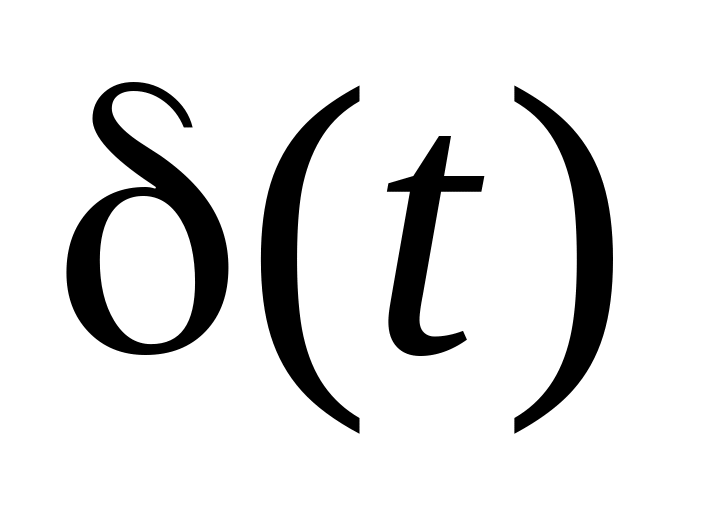
1
8
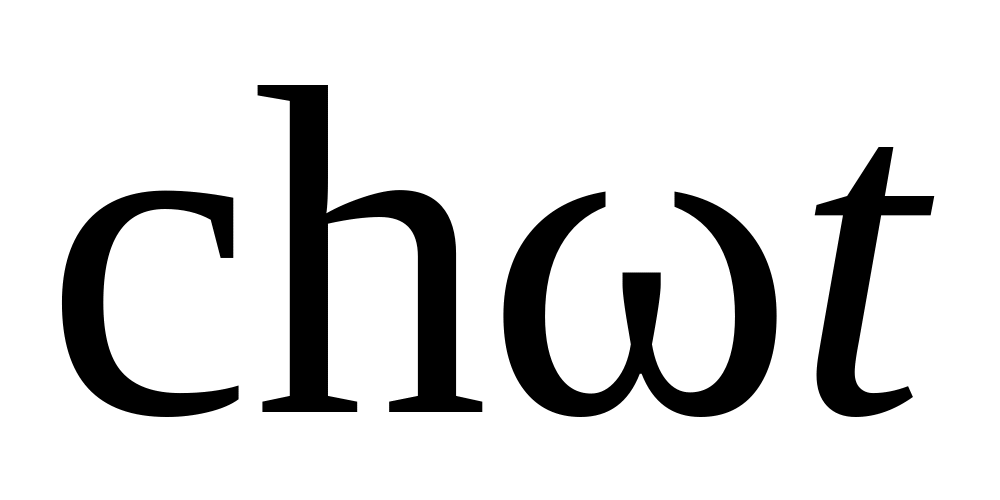
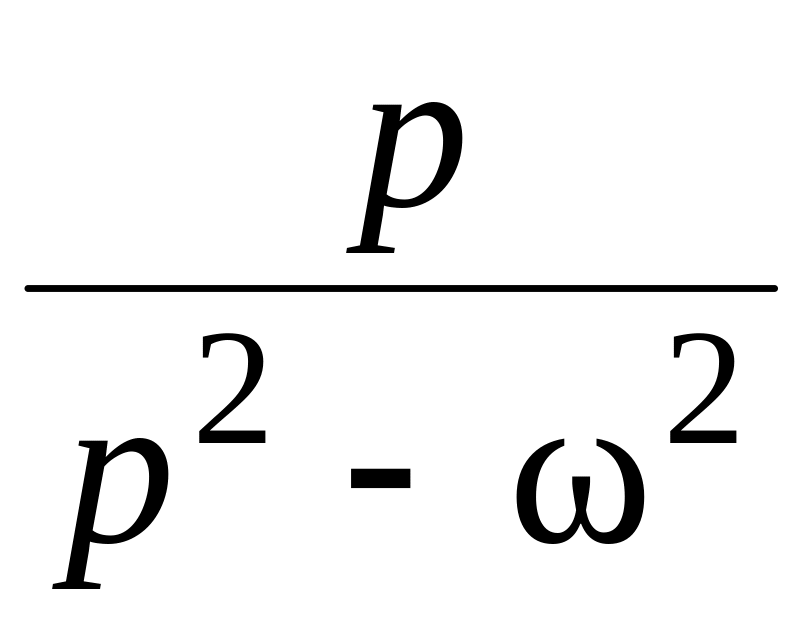
16

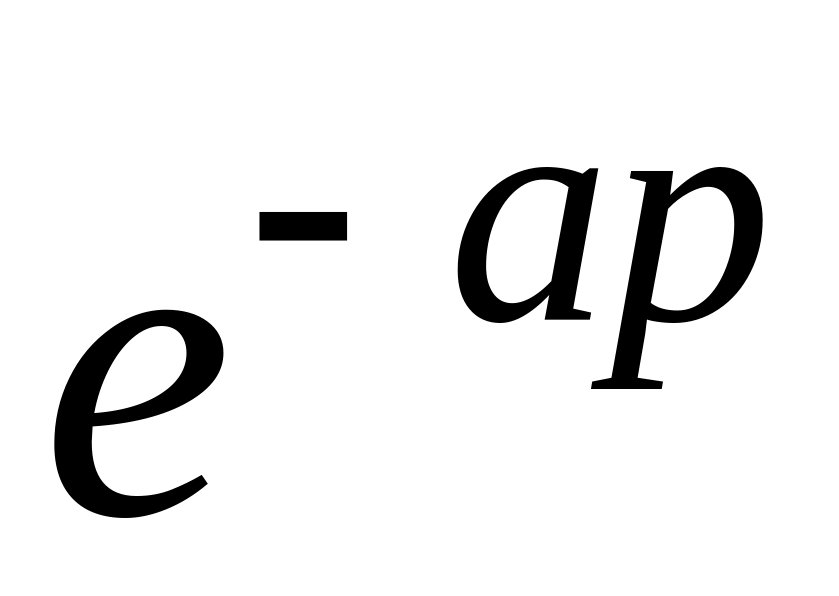
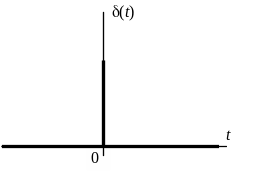
Дельта-функция. -функция Дирака (рис. 12.7) задается формулами
![]() и
и
![]() .
.
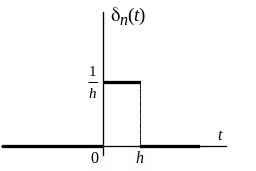
В технике -функция применяется для отображения величин, имеющих характер мгновенного импульса. Изображение (позиция 15 таблицы 1) функции Дирака, получим после предельного перехода в представлении прямоугольного импульса (рис. 12.8)
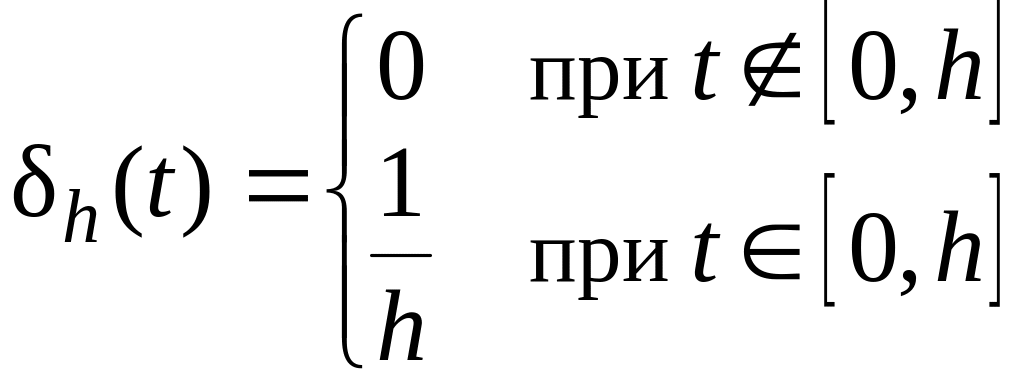
или
![]() =
= ![]() .
.
Рис. 12.7 |
Рис. 12.8 |
Отметим, что при
любом значении h
выполняется равенство
![]() .
Изображение
имеет вид
.
Изображение
имеет вид
![]() .
При h 0
функция
стремится к функции Дирака. Поэтому
.
При h 0
функция
стремится к функции Дирака. Поэтому
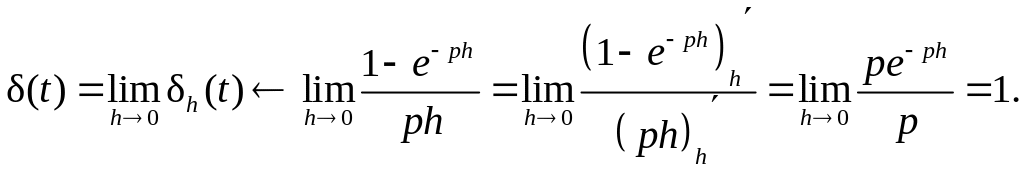
12.4 Свёртка функций
Свёрткой
![]() функций
и
функций
и
![]() на интервале
на интервале
![]() называется интеграл вида
называется интеграл вида
![]() .
.
Свёртка функций
симметрична, т.е.
![]()
![]() .
.
Теорема свёртывания
оригиналов.
Если функции
,
являются оригиналами,
![]() и
и
![]() ,
то изображение их свертки есть произведение
изображений
,
,
то изображение их свертки есть произведение
изображений
,
![]() :
:
![]()
![]() .
.
В приложениях
операционного исчисления часто
встречаются изображения вида
![]() .
Оригинал такого произведения определяется
одним из интегралов
.
Оригинал такого произведения определяется
одним из интегралов
![]()
![]()
![]()
![]()
![]() ,
,
которые называются интегралами Дюамеля.
Пример.
Найти оригинал функции F(p)=
![]() .
.
Представим F(p) в виде произведения двух сомножителей
![]() ,
,
оригиналы
которых известны
![]() .
Тогда
.
Тогда
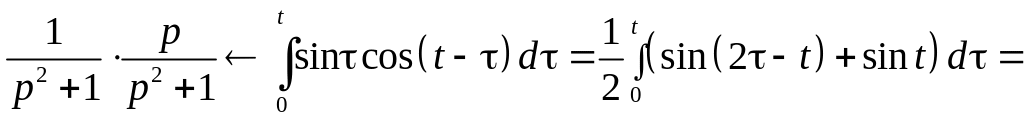
![]()
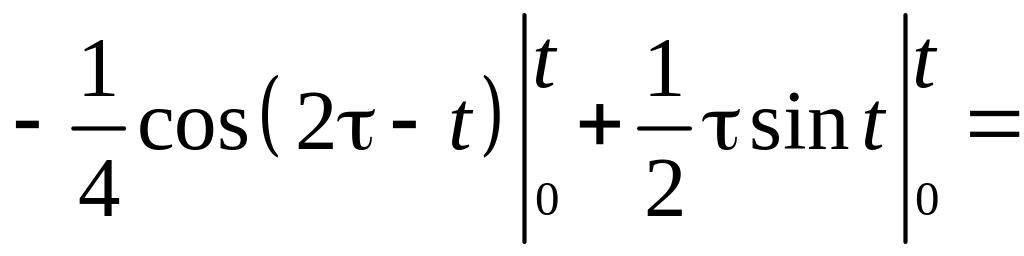
=![]()
12.5 Нахождение оригинала по изображению
На практике нахождение оригинала осуществляется сведением изображения к сумме изображений, оригиналы которых известны, и применением теоремы линейности преобразования Лапласа.
Пример.
Найти оригинал функции F(p)=
![]() .
.
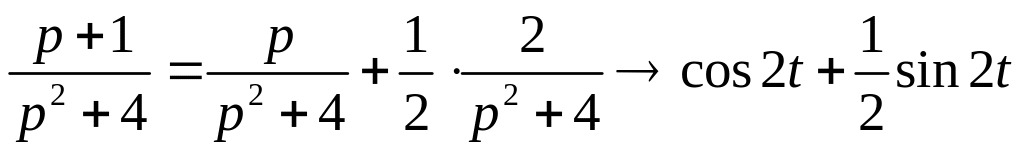 ,
,
т.к.
![]()
Имеют место две теоремы разложения, позволяющие находить оригиналы весьма широкого класса функций.
Теорема 1. Если изображение представляет собой правильную рациональную дробь
![]() ,
,
где
![]() – многочлены степени m
и n
соответственно (m
<
n),
то оригинал
есть сумма оригиналов элементарных
рациональных дробей:
– многочлены степени m
и n
соответственно (m
<
n),
то оригинал
есть сумма оригиналов элементарных
рациональных дробей:
1)
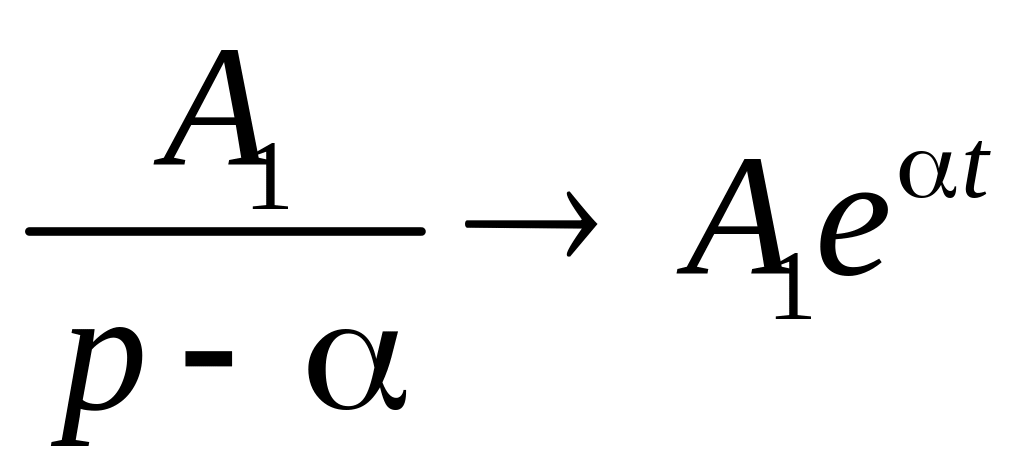 ;
;
2)
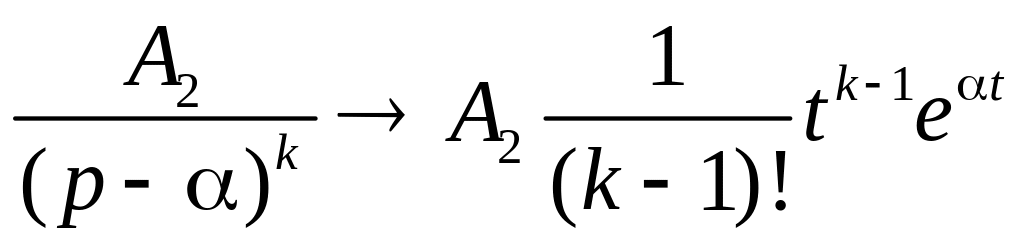 ;
;
3)
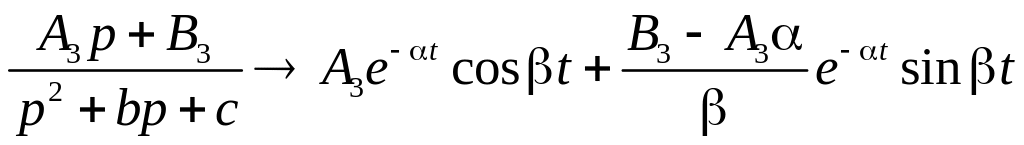 ,
(
,
(![]() .
.
Для нахождения оригинала элементарной дроби четвертого типа
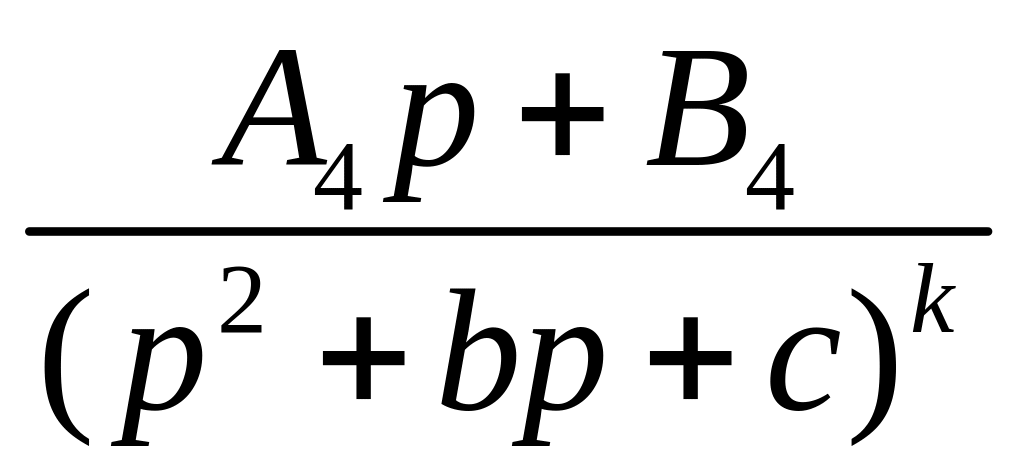 ,
,
![]()
используется свёртка оригиналов.
Пример.
Найти оригинал
изображения
![]() .
.
Рациональная дробь
![]() представляется суммой двух элементарных
дробей:
представляется суммой двух элементарных
дробей:
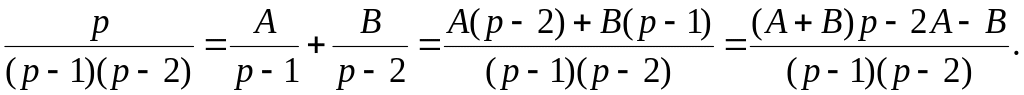 Приравнивая
числители левой и правой частей равенства,
получим
Приравнивая
числители левой и правой частей равенства,
получим
![]() .
Это равенство эквивалентно системе
.
Это равенство эквивалентно системе
![]()
решение
которой
![]() ,
,
![]() .
Следовательно,
.
Следовательно,
![]() .
.
Искомый оригинал находится по таблице 1:
![]()
Теорема
2.
Если изображение функции может быть
представлено рядом по степеням
![]() ,
,
![]() ,
,
сходящимся к , то оригинал представляется в виде степенного ряда
![]() ,
,
сходящегося при всех t.
Пример. Найти изображение ступенчатой функции, заданной на промежутке [0; +), четыре ступени которой представлены на рисунке 12.9.
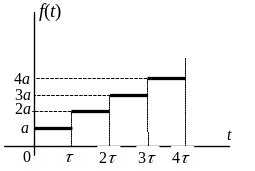
Рис. 12.9
С помощью функции
Хэвисайда
![]() можно составить аналитическое выражение
данной функции:
можно составить аналитическое выражение
данной функции:
![]()
По теореме
запаздывания имеем
![]() Слагаемые в скобках образуют бесконечную
геометрическую прогрессию с знаменателем
Слагаемые в скобках образуют бесконечную
геометрическую прогрессию с знаменателем
![]() ,
модуль которого
,
модуль которого
![]() Прогрессия сходится и её сумма
Прогрессия сходится и её сумма