11 Дифференциальные уравнения
11.1 Дифференциальные уравнения первого порядка
Дифференциальным называется уравнение, связывающее аргумент, искомую функцию и ее производные (или дифференциалы). Три формы записи дифференциального уравнения:
F(х, у, у¢) = 0; у¢ = f(х, у); Р(х, у)dx + Q(х, y)dу = 0.
Решением дифференциального уравнения называется любая дифференцируемая функция у = (х), при подстановке которой в уравнение оно обращается в тождество. График решения дифференциального уравнения называется интегральной кривой. Если существует какое-либо решение (х), то обычно существует бесконечное множество решений дифференциального уравнения, которые удается объединить единой формулой, включающей произвольную постоянную С: у = (х, С). Такое семейство функций (х, С) называется общим решением дифференциального уравнения. Равенство F(x, y, С) = 0, неявно задающее общее решение, называется общим интегралом дифференциального уравнения. Любое решение у = j(х, С0) дифференциального уравнения, полученное из общего заданием конкретного значения произвольной постоянной С = С0, называется частным решением.
Задача Коши состоит в нахождении частного решения дифференциального уравнения, удовлетворяющего начальному условию у(х0) = у0.
11.2 Основные типы уравнений первого порядка
Уравнения с разделенными переменными: Р(х)dx = Q(y)dу.
Общее решение: Р(х)dx = Q(y)dу + С.
Уравнения с разделяющимися переменными: y¢ = f(х)q(у).
y¢
= f(х)q(у)
.
Общий интеграл:
=
+ С.
Однородные
уравнения: у¢
=
.
Общий интеграл
= lnx
+ С,
где u
=
.
Линейные уравнения: у¢ + р(х)у = q(х).
Общее решение:
у
=
.
Уравнение Бернулли: у¢ + р(х)у = q(x)уn (n 0, n 1).
Это уравнение
приводится к линейному заменой
Замечание.
Решение уравнения Бернулли и линейного
уравнения может быть получено методом
Бернулли. После замены y = U(x)V(x),
y = UV + UV
неизвестная функция U(x)
равна общему решению дифференциального
уравнения
,
полученному после нахождения частного
решения V(x)
уравнения
.
Уравнение в полных
дифференциалах:
Р(х;
у)dx
+ Q(x;
y)dу
= 0 при
.
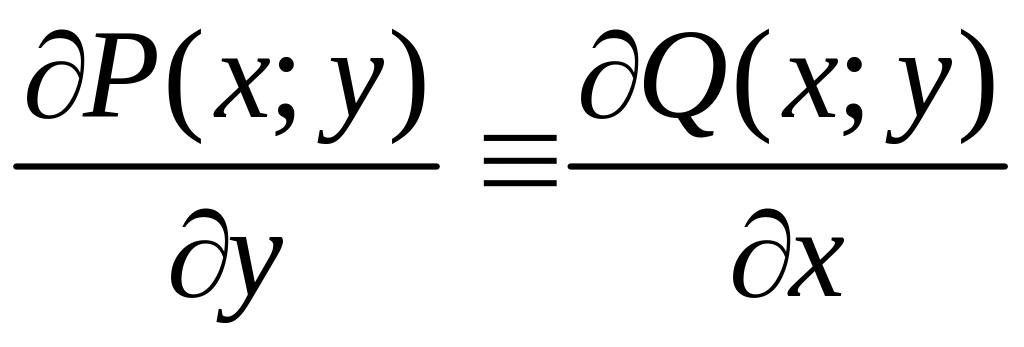Общий интеграл:
,
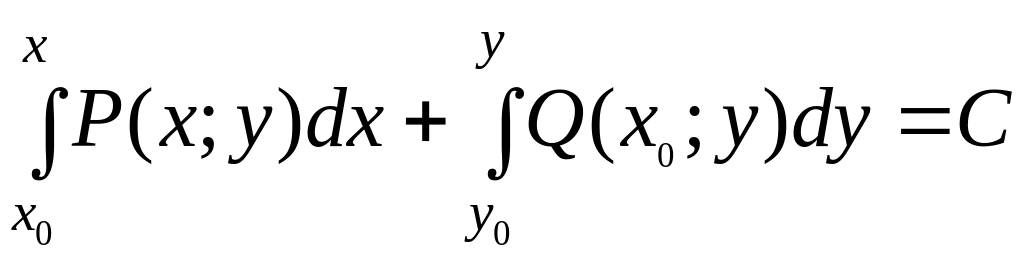где (х0;
у0)
– любая точка, в окрестности которой
существует решение дифференциального
уравнения.
Пример. Найти частное решение дифференциального уравнения
= хdх,
удовлетворяющее
начальным условиям у(2)
= 1.
= хdх – уравнение с разделенными переменными.
Общий интеграл:
=
.
Частное решение, удовлетворяющее начальным условиям х = 2, y = 1:
С0
= –3
=
–
3.
– решение задачи
Коши.
Пример. Установить тип уравнения у2у¢ + 2х – 1 = 0.
у¢ = (1 – 2х)
.
Это
уравнение
с разделяющимися
переменными.
Пример.
Найти общий интеграл уравнения у¢
–
=
.
Общий интеграл
однородного
уравнения:
=
lnx
+
С1
=
lnx
+
С1
= lnx
+ С1
(С1
= lnC).
Пример.
Найти общее решение уравнения
Для уравнения
Бернулли
(
)
сначала надо сделать замену
.
Полученное уравнение
является линейным
(
).
Общее решение:
Замечание. Решение уравнения может быть получено методом Бернулли.
Замена
y = U(x)V(x),
y = U V + UV .
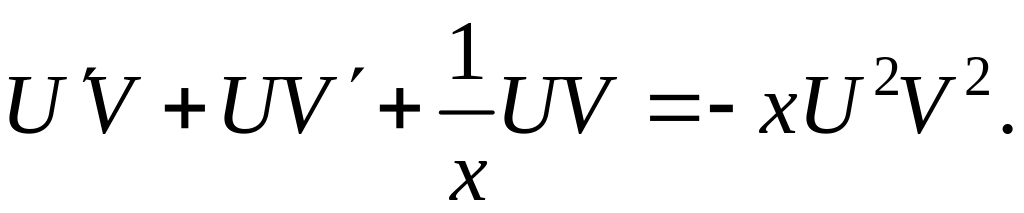
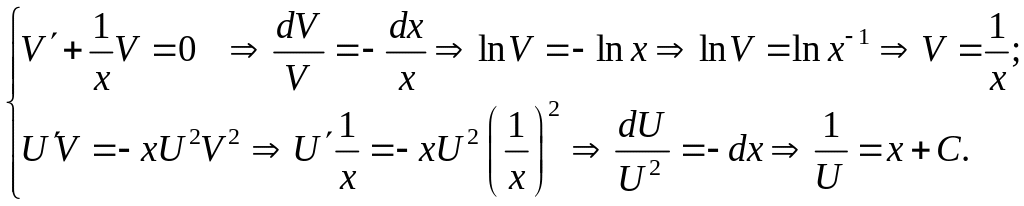
Пример. Найти общее решение уравнения
.
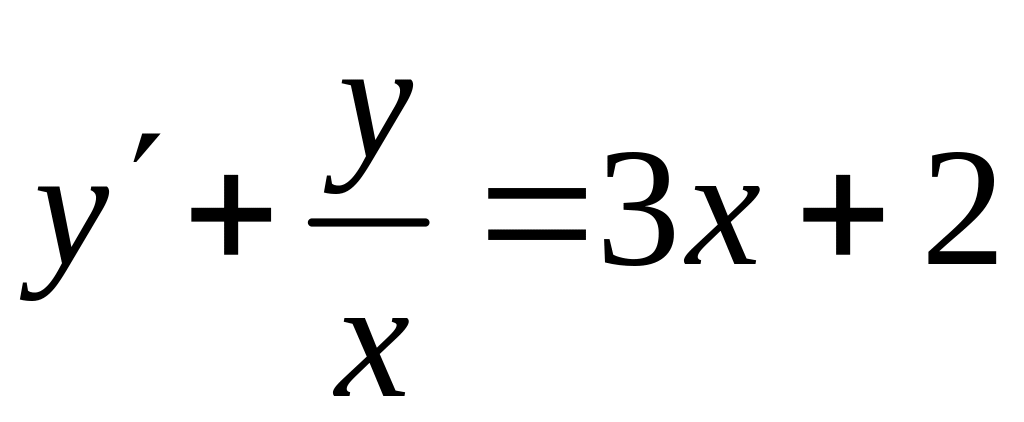Уравнение
является линейным.
;
.
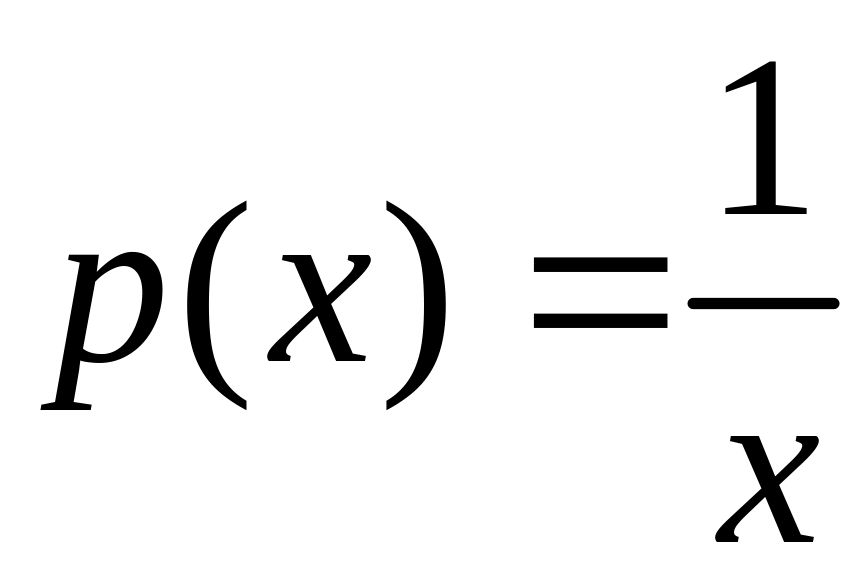После
замены y = U(x)V(x),
y = U V + UV ,
получаем
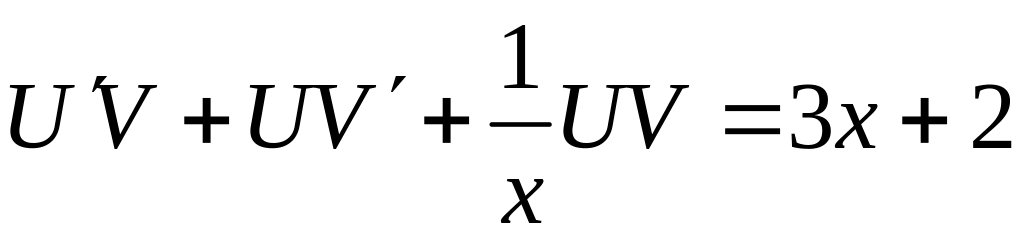или
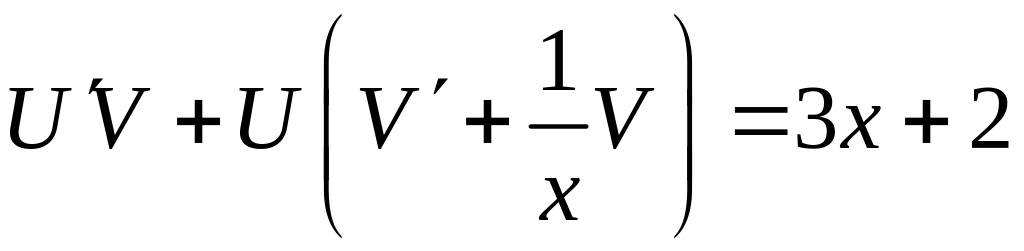
Уравнение
для определения V(x)
имеет вид
.
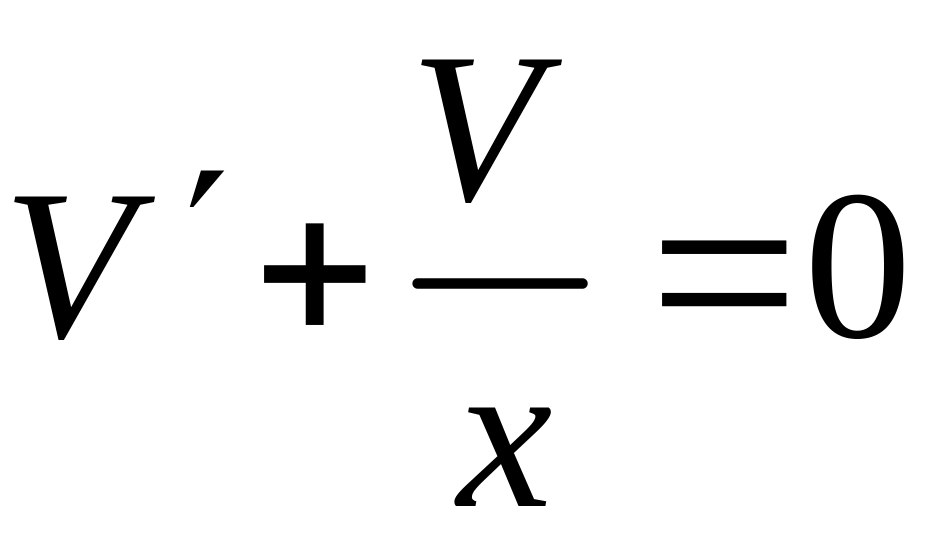Разделяя
переменные, получим
.
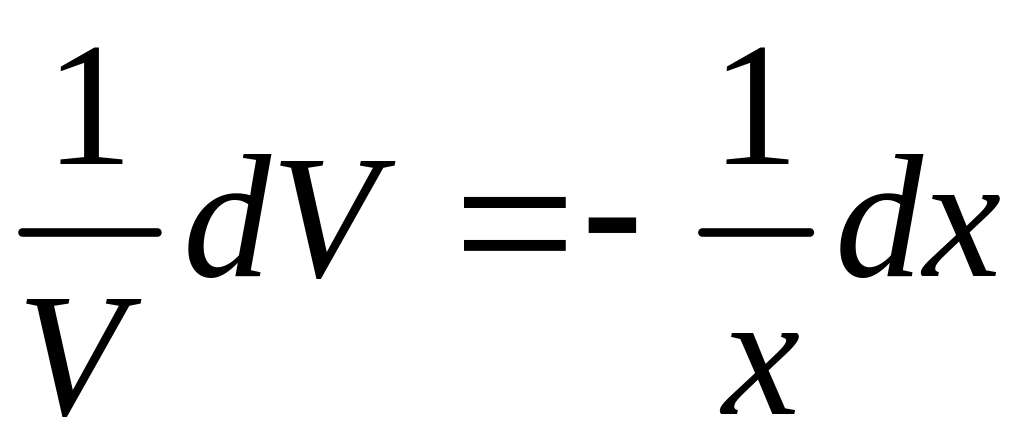Интегрируя, находим
,
откуда
.
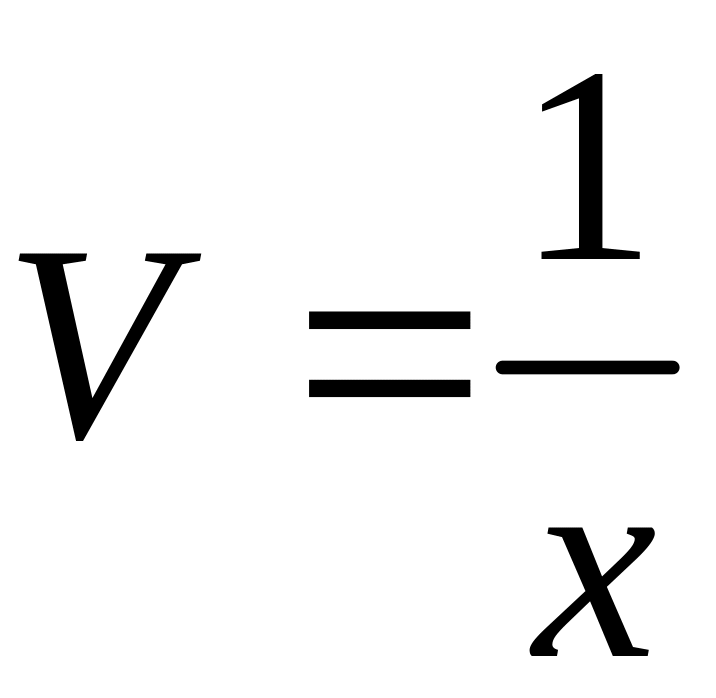Подставляя
найденное V(x)
в уравнение
,
получаем уравнение
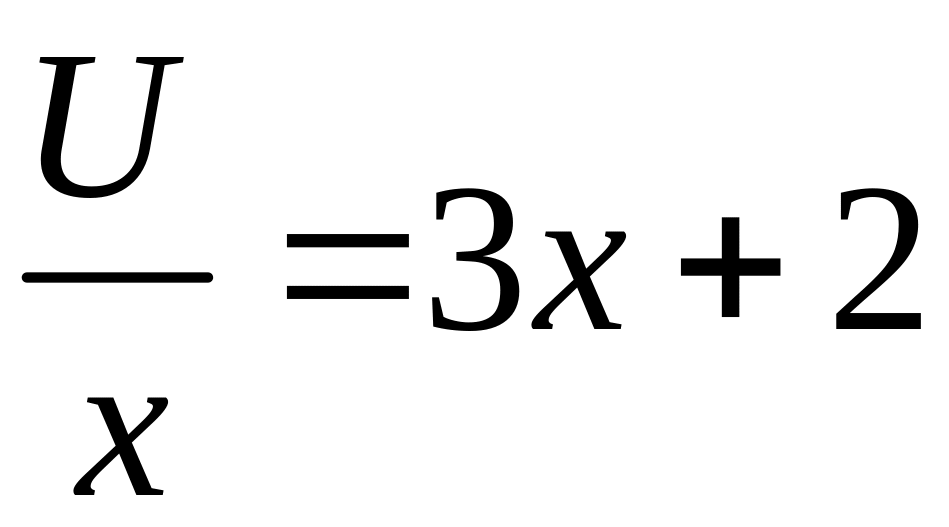для определения
.
Разделяя
переменные и интегрируя, находим
.
Тогда
.
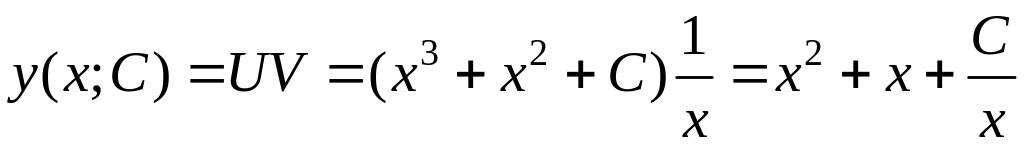Пример. Найти
общее решение уравнения
.
.
– уравнение в полных дифференциалах.
Общий интеграл:
.
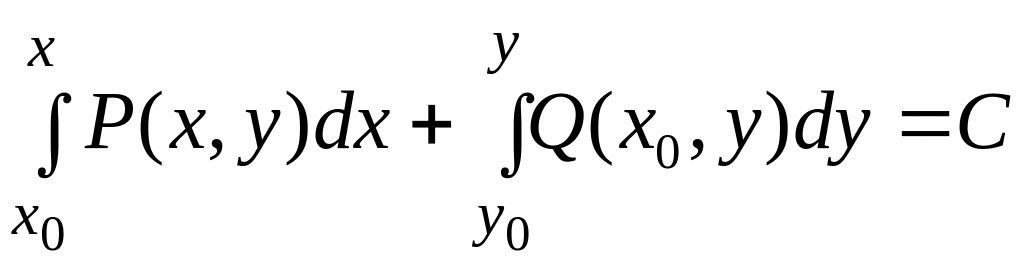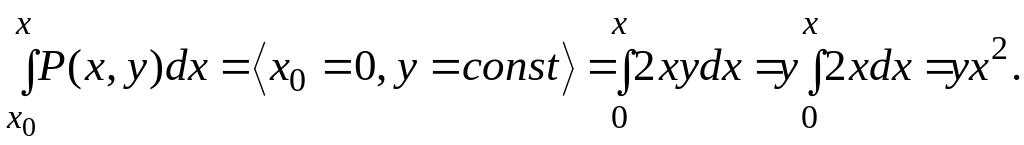
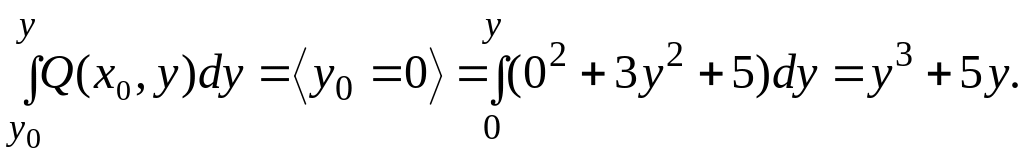
– общее решение.